---

📝堆排序

堆排序即利用堆的思想来进行排序，总共分为两个步骤：

1. 建堆
   升序：建大堆
   降序：建小堆
2. 利用堆删除思想来进行排序
   建堆和堆删除中都用到了向下调整，因此掌握了向下调整，就可以完成堆排序。

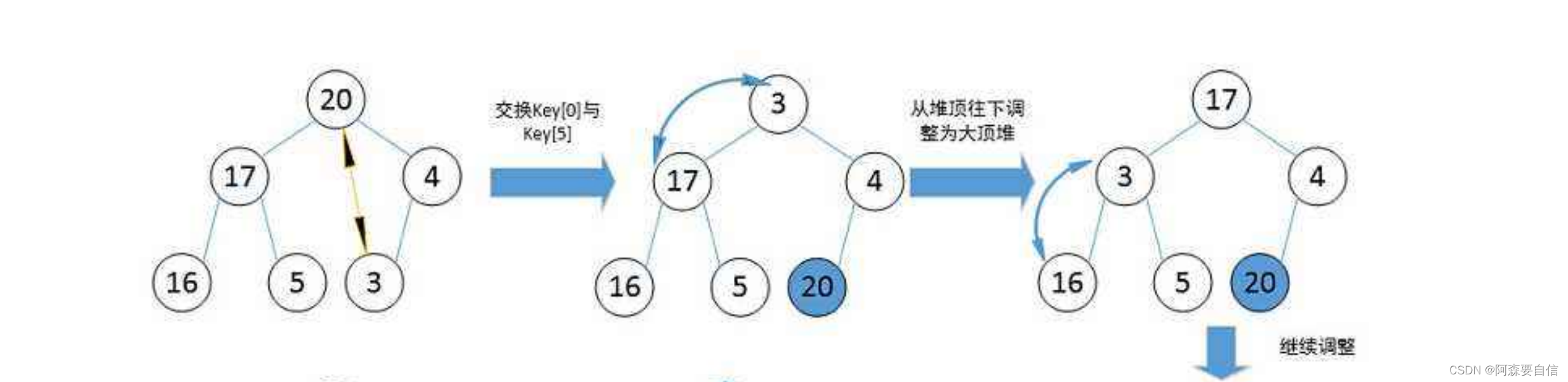
1. 堆排序代码----->升序：建大堆
   堆排序是通过建立一个大顶堆或小顶堆，然后将堆顶元素与末尾元素交换，并重新调整堆结构，这样重复地交换和调整得到有序序列。在升序排序时，我们希望第一个元素是最大的，所以需要建立大顶堆，这样堆顶元素就是当前所有元素中的最大值。

//升序，建大堆
//O(N*logN)

//定义一个交换函数，用于交换两个元素的值
void Swap(int* px, int* py)
{
	int temp = *px;
	*px = *py;
	*py = temp;
}
//将以parent为根节点的子树进行向下调整，使其满足大堆的性质
void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1; //左孩子节点的下标
	while (child < n)
	{
		//找到左右孩子节点中较大的一个
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}
		//如果孩子节点的值大于父节点的值，则交换位置
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

//堆排序函数
void HeapSort(int* a, int n)
{
	//将数组a直接建堆，使其满足大堆的性质
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}
	int end = n - 1; //用于记录堆的末尾位置
	while (end > 0)
	{
		//将堆顶元素与末尾元素交换位置，即将最大值放到末尾
		Swap(&a[0], &a[end]);
		//对除了末尾元素外的部分进行向下调整，使其满足大堆的性质
		AdjustDown(a, end, 0);
		end--;
	}

}
int main()
{
	int a[] = { 3,9,5,2,7,8,10,1,4 };
	printf("堆升序前\n");
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		printf("%d ", a[i]);
	}
	//堆升序，建大堆
	HeapSort(a, sizeof(a) / sizeof(int));
	printf("\n堆升序后\n");
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
	return 0;

}

代码运行：

1. 堆排序代码----->降序：建小堆
   而在降序排序时，我们希望第一个元素是最小的。如果还建立大顶堆，那么堆顶元素会是最大值，这与我们希望的降序结果不符。所以在降序排序时，我们需要建立一个小顶堆。这样堆顶元素就是当前所有元素中的最小值，和我们希望的降序结果一致。通过每次交换堆顶(最小值)和末尾元素，可以实现数组从小到大排列，也就是降序排序结果。

#include <stdio.h>
// 交换两个元素的值
void Swap(int* px, int* py)
{
	int temp = *px;
	*px = *py;
	*py = temp;
}
// 将以parent为根节点的子树调整为小堆
void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1; // 左孩子节点的下标
	while (child < n)
	{
		// 找到左右孩子节点中值较小的节点
		if (child + 1 < n && a[child + 1] < a[child])
		{
			child++;
		}
		// 如果子节点的值小于父节点的值，则交换父子节点的值
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
// 堆排序
void HeapSort(int* a, int n)
{
	// 建堆：从最后一个非叶子节点开始，依次向上调整子树为小堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}
	int end = n - 1; // 堆的最后一个元素的下标
	while (end > 0)
	{
		// 将堆顶元素（最小元素）与堆的最后一个元素交换位置
		Swap(&a[0], &a[end]);
		// 将除了最后一个元素之外的部分重新调整为小堆
		AdjustDown(a, end, 0);
		end--;
	}

}
int main()
{
	int a[] = { 3,9,5,2,7,8,10,1,4 };
	printf("堆降序前\n");
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		printf("%d ", a[i]);
	}
	// 使用堆排序进行降序排序
	HeapSort(a, sizeof(a) / sizeof(int));
	printf("\n堆降序后\n");
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
	return 0;

}

🌠 TOP-K问题

TOP-K问题是数据挖掘和信息检索中的一个重要问题。

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。
TOP-K问题是数据挖掘和信息检索中的一个重要问题。

TOP-K问题的含义是:给定一个集合,找出其中值最大或最小的前K个元素。

常见的TOP-K问题有:

1. 查找文档集合中与查询条件最相关的前K篇文档。这在搜索引擎中很常见。

2. 从用户评分最高的物品中找出前K个最受欢迎的物品。

3. 从数据库中找出收入前K高的用户。

4. 从候选人中找出支持率前K高的候选人，专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。。

TOP-K问题的一般解法包括:

• 排序法:直接对全集排序,取前K个元素。时间复杂度O(nlogn)
• 堆排序法:使用小顶堆或大顶堆维护前K个元素,时间复杂度O(nlogk)
• 选择算法:每次选择当前值最大/小的元素加入结果集,时间复杂度O(nlogk)
• 空间优化算法:如QuickSelect,找到第K个元素的位置而不是排序全集。
• 桶排序法:如果值范围有限,可以使用桶排序提升效率。
• 索引支持的算法:如果有索引支持,可以利用索引更快找出TOP-K,如B+树。

对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决，基本思路如下：

1. 用数据集合中前K个元素来建堆
   前k个最大的元素，则建小堆
   前k个最小的元素，则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素
   将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。

🌠造数据

首先我们要TOP-K，那得有数据，先来生成数据，那就生成随机数据到文件。

void CreateNData()
{
	//造数据
	int n = 100000;
	srand(time(0));//使用时间作为随机数种子
	const char* file = "data.txt";//数据文件名
	FILE* fin = fopen(file, "w");//打开文件用于写入
	if (fin == NULL)//检查文件是否打开成功
	{
		perror("fopen error");//输出打开错误信息
		return;
	}

	for (int i = 0; i < n; ++i)//循环写入n行数据
	{
		int x = (rand() + i) % 1000000;//生成0-999999之间的随机数
		fprintf(fin, "%d\n", x);//写入一行数据
	}
	// 别忘了关闭文件哦
	fclose(fin);
}

rand()函数产生的随机数范围是0-RAND_MAX，在C/C++标准库中,rand()范围是0到32767
i的范围是0-9999,因为n定义为10000，所以rand()结果加i范围是:0 + 0 = 0，32767 + 99999 =132,766，没有超过1000000，但取余可以实现随机数更均匀地分布在0-999999范围内

🌉topk找最大

1、用前10个数据建小堆
2、后续数据跟堆顶数据比较，如果比堆顶数据大，就替代堆顶，进堆

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
#include <string.h>
#include <time.h>

void Swap(int* px, int* py)
{
	int tmp = *px;
	*px = *py;
	*py = tmp;
}


void AdjustDown(int* a, int n, int parent)
{ //a是数组指针,n是数组长度,parent是当前需要下调的父结点索引

	int child = parent * 2 + 1;
	//child表示父结点parent的左孩子结点索引,因为是完全二叉堆,可以通过parent和2计算得到

	while (child < n)
	{
		//如果左孩子存在

		if (child + 1 < n && a[child + 1] < a[child])
		{
			//如果右孩子也存在,并且右孩子值小于左孩子,则child指向右孩子
			child++;
		}
		if (a[child] < a[parent])
			//如果孩子结点值小于父结点值,则需要交换
		{
			Swap(&a[child], &a[parent]);
			//交换孩子和父结点
			parent = child;
			//父结点下移为当前孩子结点

			child = parent * 2 + 1;

			//重新计算新的左孩子结点索引

		}
		else
		{
			break;
		}
	}
}
void topk()
{
	printf("请输入k->");
	int k = 0;
	scanf("%d", &k);
	const char* file = "data.txt";
	//打开文件
	FILE* fout = fopen(file, "r");
	if (fout == NULL)
	{
		perror("malloc fail");
		return;
	}
	//临时变量读取文件数据 
	int val = 0;
	//分配内存用于保存最小堆
	int* minheap = (int*)malloc(sizeof(int) * k);
	if(minheap ==NULL)
	{
		perror("malloc fail");
		return;
	}
	//初始化堆,读取文件前k个数据构建最小堆
	for (int i = 0; i < k; i++)
	{
		fscanf(fout, "%d", &minheap[i]);
	}
	
	//建个小堆
	for (int i = (k - 1 - 1) / 2; i >=0; i--)
	{
		AdjustDown(minheap, k, i);
	}

	int x = 0;
	while (fscanf(fout, "%d", &x) != EOF)
	{
		//读取剩余数据，比对顶的值大，就替换他进堆
		if (x > minheap[0])
		{
			//替换堆顶值,并调用下滤调整堆结构
			minheap[0] = x;
			AdjustDown(minheap, k, 0);
		}
	}

	for (int i = 0; i < k; i++)
	{
	    //输出堆中保存的前k个最大值 
		printf("%d ", minheap[i]);
	}
	printf("\n");
	fclose(fout);

}

int main()
{
	CreateNData();
	topk();
}

输出：

的确是五个数，怎么验证他是10万个数中最大的那五个数呢？
OK!用记事本打开该文件的data.txt，随机找五个数改大点，比如到百万，再运行，能不能找出这五个数，能就对了。

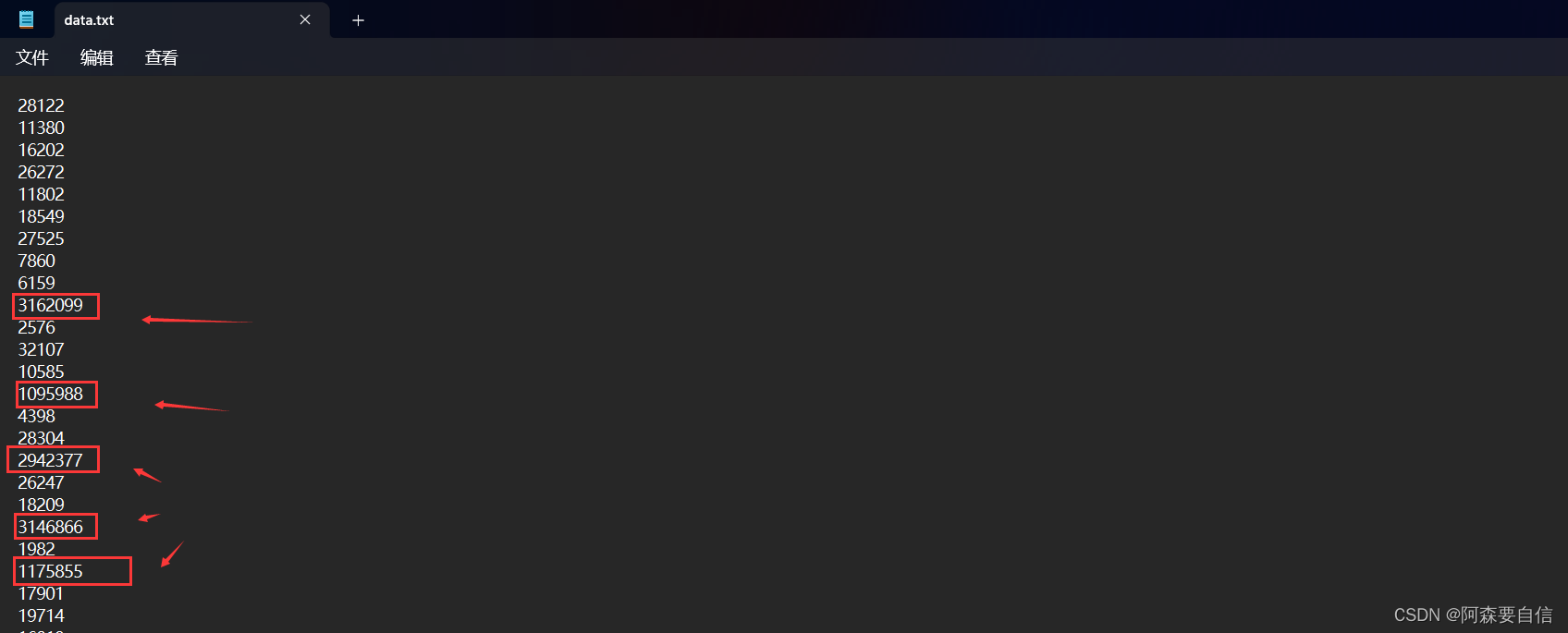
再次运行效果图：

---

🚩总结

感谢你的收看，如果文章有错误，可以指出，我不胜感激，让我们一起学习交流，如果文章可以给你一个小小帮助，可以给博主点一个小小的赞😘