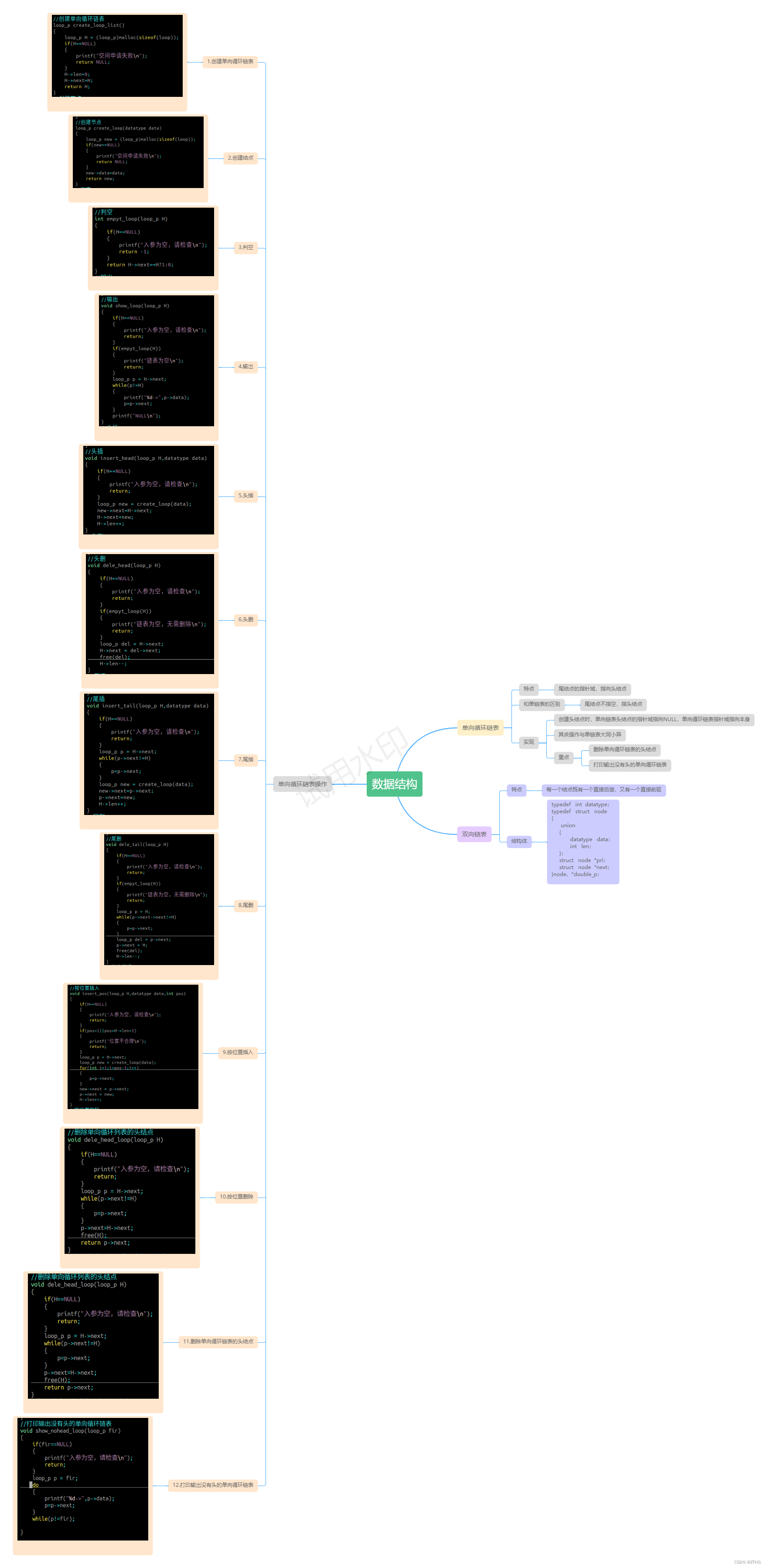
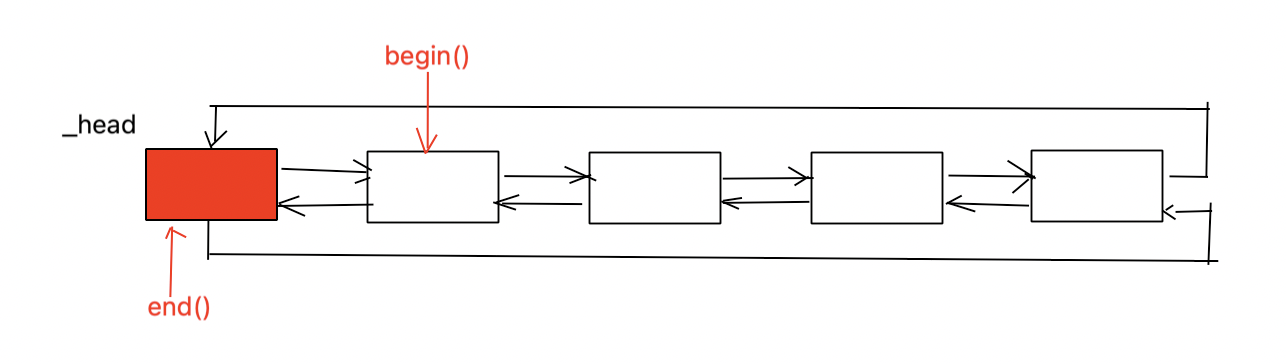
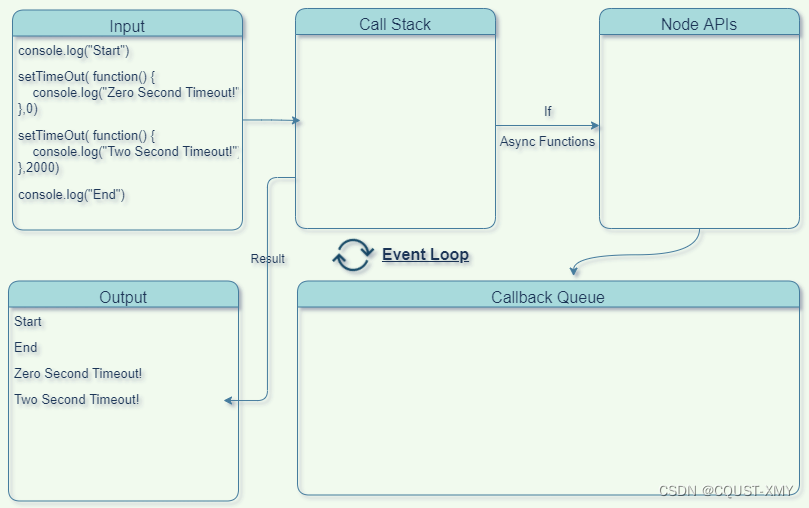
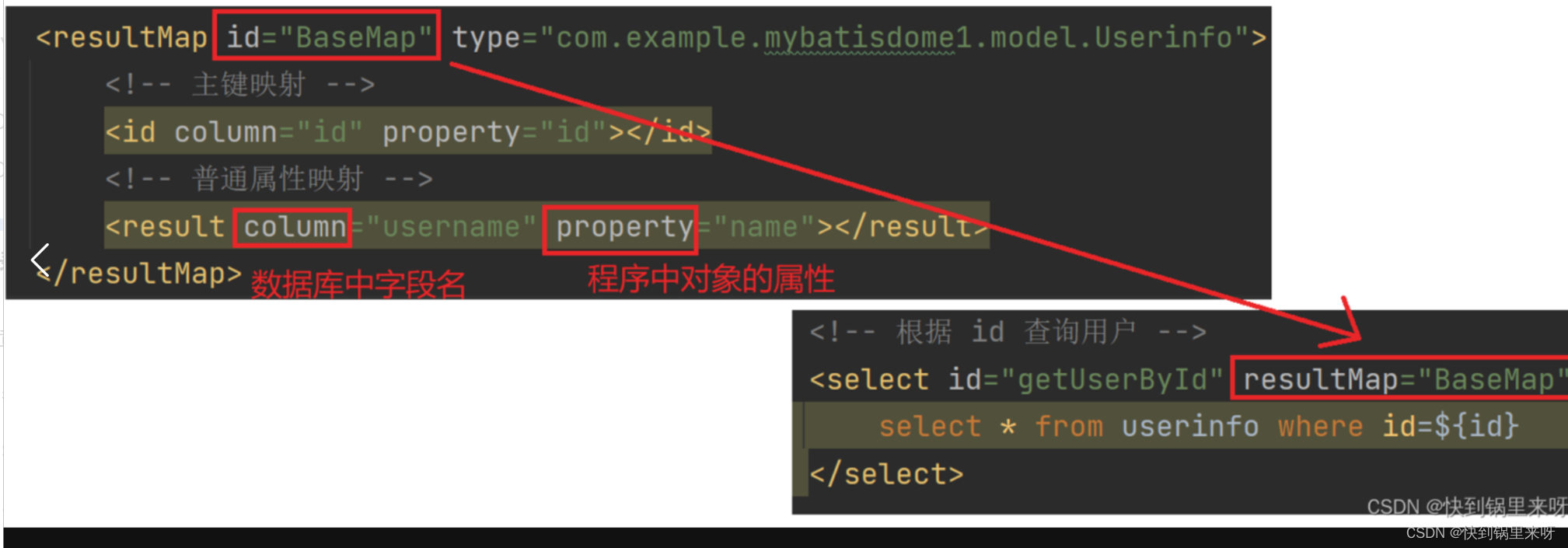
问题描述：

---

解题思路：

        可以先求出1~1e6每个位置是否有解，后计算前缀和再求出不同区间的和。（时间复杂度小）

         进行dfs操作：依次组合1~1e6所有元素。并计算每一个组合的乘积，在该乘积位置的cnt加一。但只是这样做肯定会超时，因此我们需要进行剪枝。剪枝有以下三种情况：

        1.当乘积在中途就超过1e6。

        2.假设三元组递增，则枚举下限。（st）

        3.计算上限公式，减小枚举上限。（up）由下图推导的组合元素的上限公式。

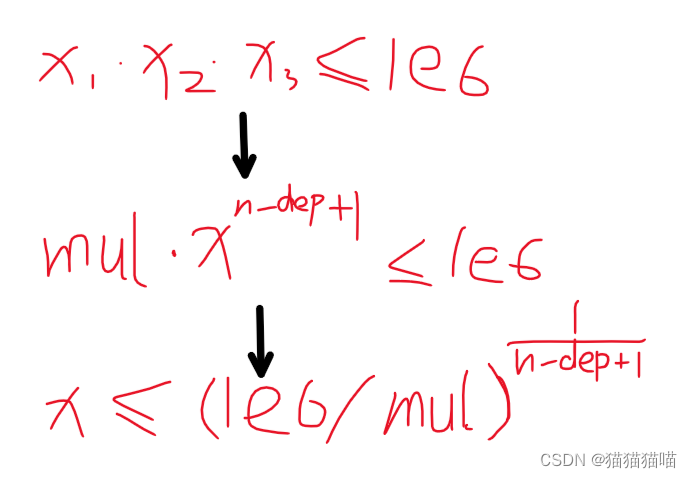
        注意点： 

                因为默认三元组元素递增，有根据三角形两边和大于第三边，所以当枚举第三层时需要判断是否比前两个元素之和小，用到sum计算前2个和并使第三层的上限小于sum。

---

题解：        

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 9;
int cnt[N], prefix[N];  // cnt[i]:是否有乘积为i的组合，若有则为1，无为0。prefix[]:前缀和 

void dfs(int dep, int st, int mul, int sum)  // dep:当前元素(层) 。st:前一个元素值。mul:前面元素的乘积。sum:前元素的和
{
	if(mul > 1e6)return;  // 剪枝一
	
    if(dep == 4)  // 出口
	{
		cnt[mul]++;
		return;
	}
	
	int up = pow(1e6 / mul, 1.0 / (3 - dep + 1)) + 3;  // 可以宽松一点，加3。剪枝二
	
	for(int i = st + 1; i < (dep == 3 ? sum : up); i++)  // 注意当枚举第三层时需要判断是否比前两个元素之和小。剪枝三
	{
		dfs(dep + 1, i, mul * i, sum + i);
	}
}

int main()
{
  ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	dfs(1, 0, 1, 0);
	
	for(int i = 1; i <= 1e6; i++)prefix[i] = prefix[i - 1] + cnt[i]; 
	
	int q;cin >> q;
	
	while(q--)
	{
		int l, r;cin >> l >> r;
		cout << prefix[r] - prefix[l - 1] << '\n';	
	} 
	
	return 0; 
}

---

知识点：dfs,剪枝