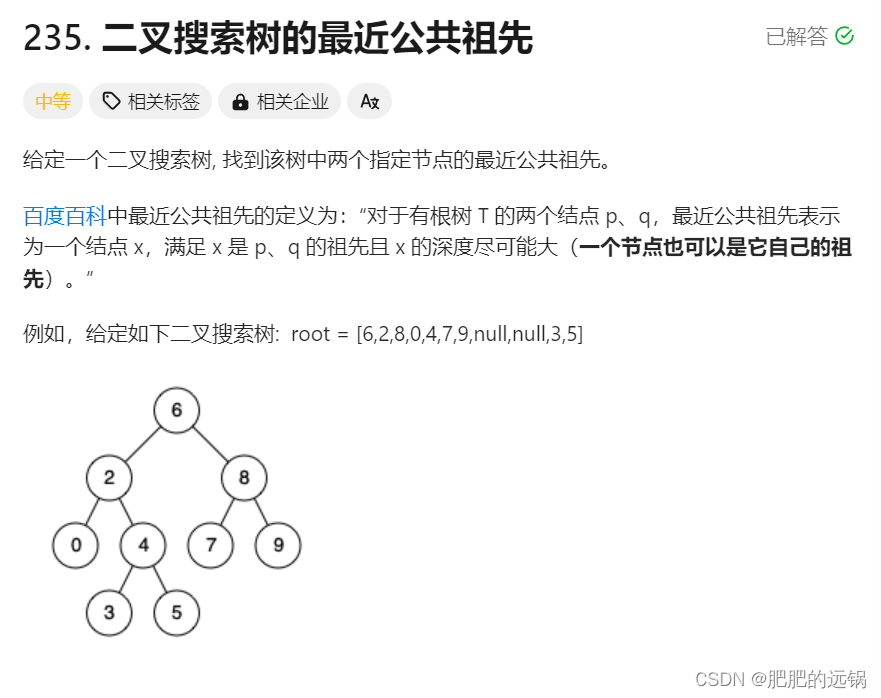
这道题和寻找二叉树的最近祖先可以用同一套解法，也就是说，考虑当你站在一个节点上的时候，应该干啥：看当前节点是不是指定的孩子p，q，然后检查左子树有无指定节点，检查右子树有无指定节点，那天然就是一个后序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

class Solution {
public:
    TreeNode* res = NULL;
    bool traceback(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == NULL) {
            return false;
        }

        bool leftRes = traceback(root->left, p, q);
        bool rightRes = traceback(root->right, p, q);
        bool rootRes = (root == p || root == q) ? true : false;

        if (rootRes == true) {
            if (leftRes == true && rightRes == true) {
                if (res == NULL) {
                    res = root;
                }
                return true;
            } else if ((leftRes == true) || (rightRes == true)) {
                if (res == NULL) {
                    res = root;
                }
                return true;
            } else{
                return true;
            }

        } else {
             if (leftRes == true && rightRes == true) {
                if (res == NULL) {
                    res = root;
                }
                return true;
            } else if ((leftRes == true) || (rightRes == true)) {
                return true;
            } else{
                return false;
            }
        }
        return false;
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        traceback(root, p, q);
        return res;
    }
};

这道题自然是有除了二叉树通解以外的解法的，实际上，BST的大小关系是可以指示检索方向的，根据BST性质去检索各个节点，当发现某个节点的值恰好处于p，q之间时，这个节点就是最近公共祖先

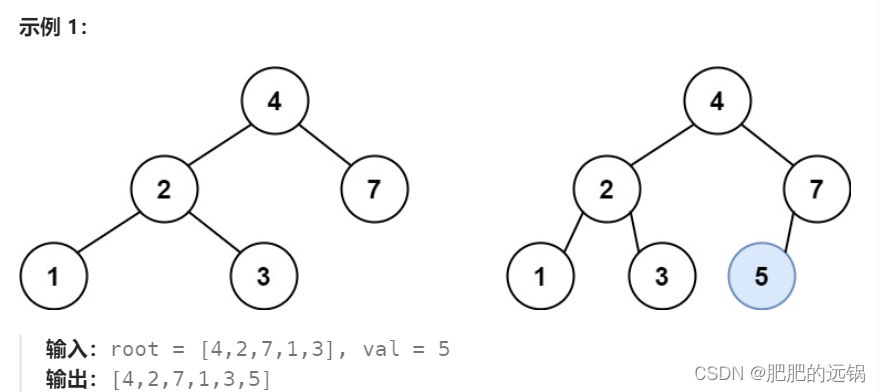
二叉搜索树顺序搜索，遇到第一个可以插入的位置直接插就行

/**
 1. Definition for a binary tree node.
 2. struct TreeNode {
 3.     int val;
 4.     TreeNode *left;
 5.     TreeNode *right;
 6.     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 7.     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 8.     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 9. };
 */
class Solution {
public:
    void traceback(TreeNode* root, const int &val){
        if(root == NULL){
           return;
        }
        
        if(root->val > val){
            if(root->left != NULL){
                traceback(root->left,val);
            }else{
                TreeNode * node = new TreeNode(val);
                root->left = node;
                return;
            }           
        }else if(root->val < val){
             if(root->right != NULL){
                traceback(root->right,val);
            }else{
                TreeNode * node = new TreeNode(val);
                root->right = node;
                return;
            }          
        }       
    }
    TreeNode* insertIntoBST(TreeNode* root, int val) {
         if(!root){
           TreeNode * node = new TreeNode(val);
           root = node;
         }
         traceback(root,val);
         
         return root;
    }
};

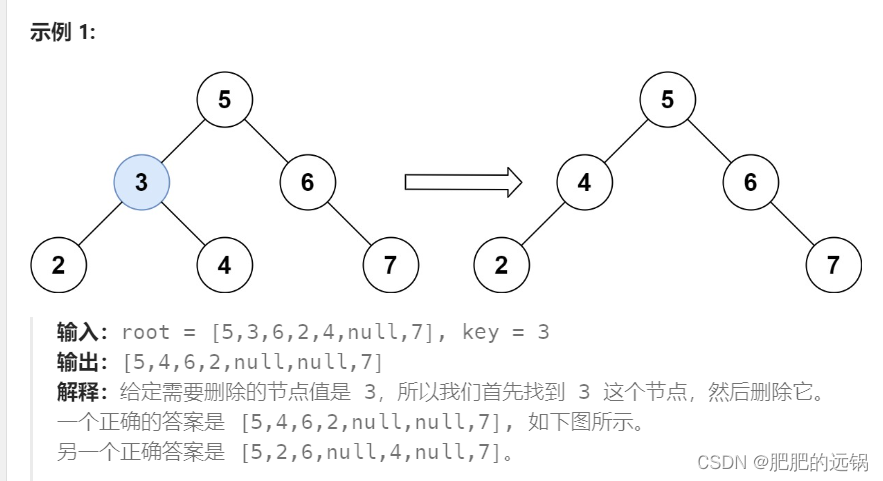
这道题，实际上是一个先序遍历的遍历结构，但是先序遍历找到对应的节点以后有四种情况需要处理：

1. 找到的节点是叶子节点，直接删除，父节点指NULL
2. 找到的节点是只有右子树，无左子树，这时候直接跳过这个节点，把存在的子树接到父节点下
3. 同理。找到的节点是只有左子树，无右子树，这时候直接跳过这个节点，把存在的子树接到父节点下
4. 找到的节点左右子树都不为空，做一个子树的右旋操作，左子树接到右子树的最左节点上，这个时候被删除节点的左子树被移动后，原位置为空，问题就变成了只有右子树无左子树的问题

我们在返回时需要确定待删除节点是在父节点的左子树还是右子树，这个就太麻烦了，直接递归式构造遍历即可

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
          if(root == NULL){
              return NULL;
          }
          
          if(root->val == key){
              if(root->left == NULL && root->right == NULL){
                  return NULL;
              }else if(root->left == NULL && root->right != NULL){
                  return root->right;
              }else if(root->left != NULL && root->right == NULL){
                  return root->left;
              }else{
                  TreeNode * node = root->right;
                  while(node != NULL){
                      if(node->left == NULL){
                          node->left = root->left;
                          break;
                      }
                      node = node->left;
                  }
                  return root->right;
                  
              }
          }
          if(root->val > key) {root->left = deleteNode(root->left,key);}
          if(root->val < key) {root->right = deleteNode(root->right,key);}
        return root;
    }
};