Leetcode.242 有效的字母异位词：

242. 有效的字母异位词 - 力扣（LeetCode）

       原理简单，首先判断给定的两个字符串的长度是否相等，如果不相等则直接返回，只有在给定字符串长度想的的情况下才进行下一步的判断。

      当给定的元素相等时，首先创建名为，的两个数组，数组大小为，并且对，字符串进行遍历，在遍历的过程中，使位置的数值++，位置的数值++。

      遍历两个数组，如果出现了的情况，则直接返回。遍历结束后返回。对于代码如下：

class Solution {
public:
    bool isAnagram(string s, string t) {

        int hash[26] = {0};
        int hash1[26] = {0};

        if( s.size() != t.size())
        {
            return false;
        }

        for(size_t i = 0; i < s.size(); i++)
        {
            hash[s[i]-'a']++;
            hash1[t[i]-'a']++;
        }

        for(int j  = 0; j < 26; j++)
        {
            if(hash[j] != hash1[j])
            {
                return false;
            }
        }

        return true;

    }
};

运行结果如下：

(注:在下面给出的题目解析中，会涉及到的使用，由于作者本人水平有限，并不能给出关于这两种数据结构的相关解释，因此只给出使用方法，对于这两种数据结构进行解析的文章，将在年月之前给出。）

Leetcode.349 两个数组的交集:

349. 两个数组的交集 - 力扣（LeetCode）

       本题虽然使用会更加方便，但是并不是刚性要求，因此介于作者水平有限，将使用进行解答：

      首先创建一个大小大于的数组，遍历数组，使得。在遍历完成后，遍历另一个数组，如果，则说明该该数值在种出现过，需要进行记录。

      对于如何记录，可以创建一个类型的对象，如果出现了满足上面给出的条件的数据，则通过_函数进行插入。并且，为了满足交集的性质，即：集合中不能出现重复的元素。需要进行去重。

      去重的方法如下：在进行了_操作后，则令。后续再遇到相同的元素时，便不会向种进行尾插，达到了去重的目的。对于代码如下：
 

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {

     int hash[1001] = {0};

     for(int i = 0; i < nums1.size(); i++)
     {
        hash[nums1[i]] = 1;
     }

     vector<int> result;
    
     for(int j = 0; j < nums2.size(); j++)
     {
        if(hash[nums2[j]] == 1)
        {
            result.push_back(nums2[j]);
          
            hash[nums2[j]] = 0;
        }
     }

     return result;

    }
};

运行结果如下：

Leetcode.202 快乐数：

202. 快乐数 - 力扣（LeetCode）

       对于本题，难点在于理解题干中的信息。对于快乐数的定义，题目中已经给了的样例，因此不再进行过多解释。但是在题干中，提到了在求快乐数的过程中，将这个数替换为每个位置上的数字的平方和的过程是无限循环的，例如文章给定一个数，则求解是否为快乐数的过程可以由下图表示：

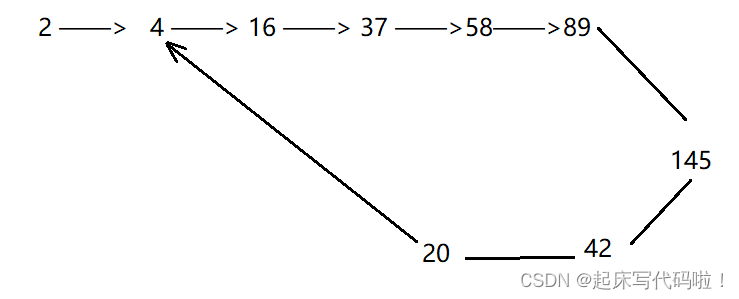
而对于题目中给的样例，求解其是否是快乐数的过程如下：

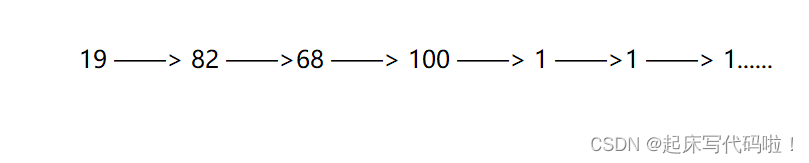
不难发现，当一个数经过若干次计算，得到的结果为时，则后续的结果便是无限循环，因此，也可以把这个过程看作上面菲快乐数的成环过程，即：

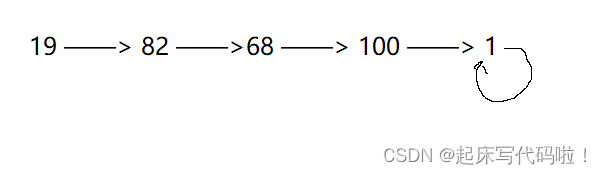
       不过上面给出的例子只是两个个例，并不具备普遍性，由此会引起一个问题：对于一个数,可以是任意一个正整数，均存在上面的环状循环过程吗？对于这一过程，下面将使用鸽巢原理进行证明：

      对于鸽巢原理，其大体内容为：存在个巢，个鸽子，则必定存在一个巢，里面的鸽子数量，假设取一个数为，即个数位上都是。如果对这个最大的数值进行一次上面的操作，则不难得出，这个数是一定小于的，因此，对于这个数据在求解快乐数时产生的数据的范围一定是，假设，每进行一次上方的运算，都会得到一个属于上面区间中的不同的数值，那么，在进行次操作后，一定会得到一个和之前某次运算得到的值相同的值。因此，如果运算次数够多，对于任何一个数，均存在一个无限循环。

     在证明了一定会出现环状循环后，便可以进行解题：

       首先创建一个函数用于进行一次上面计算欢乐数的过程，这里将这个函数命名为，并且创建一个变量用于接收函数的返回值，这里将这个变量命名为。通过创建一个哈希表，这里命名为。

      每进行一次计算，便进行一次判断，如果，则说明是快乐数，返回，如果不是，则首先查找这个数是否在中出现过，如果出现过，则说明进入了上图中非快乐数的死循环，返回，反之则将这个数存放在中。具体代码如下：

class Solution {
public:
    
    int multvalue(int n)
    {
        int sum = 0;
        int t = 0;
        while(n)
        {
            t = n%10;//取n的最小位上的数
            sum += t*t;//
            n = n/10;//去掉最小位

        }
        return sum;
    }
    bool isHappy(int n) {
        unordered_set<int> hash;

        int value = n;
        while(1)
        {
            value = multvalue(value);

            if(value == 1)
            {
                return true;
            }

            if( hash.find(value) != hash.end())
            {
                return false;
            }
            else
            {
                hash.insert(value);
            }
        }

    }
};

运行结果如下：

    

Leetcode.1 两数之和—梦开始的地方：

1. 两数之和 - 力扣（LeetCode）

        对于本题，依然可以使用哈希的思想进行解题，具体如下：
        首先利用创建一个哈希表，具体结构为：第一个位置存放数值，第二个位置存放该数值所对应的下标。同时创建一个类型的对象用于存储返回值首先对给定的进行遍历，每当遍历一个数值时，在哈希表中对这个数值进行查询。此时会出现两种情况：

        如果存在这个数，则表示找到了这个数，同时将这个数所对应的数值以及下标插入到中，返回。

      如果不存在,则将这两个数值插入到哈希表中。循环上述过程。

下面将通过一组例子，来对上述过程进行图像化的说明：

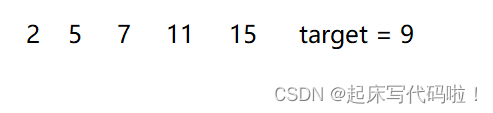
     例如，给定上图所示的数字，且需要查找的目标和为，在进行循环时，首先对数组的第一个元素进行判断，即：去哈希表中，找是否存在这个数，此时不存在，则向哈希表中插入,即：

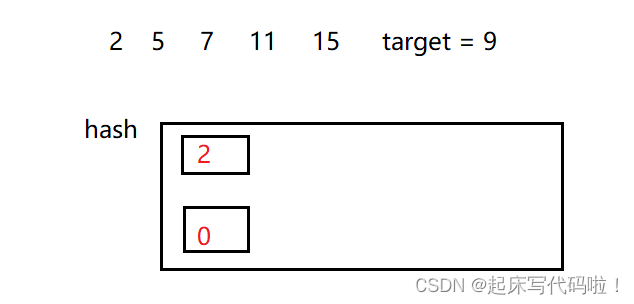
       对元素进行判断，查找哈希表中是否存在这个数值，由于不存在，因此，向哈希表中插入，即：

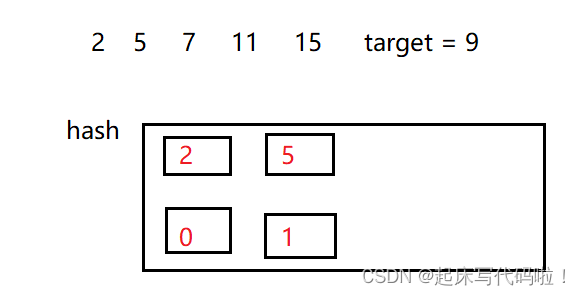
       对元素进行判断，查找哈希表中是否存在这个数值，此时存在，则向中插入这两个数的下标，即。返回。对应代码如下：

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
         std::unordered_map <int,int> hash;
         vector<int> v;

         for(size_t i = 0; i < nums.size(); i++)
         {
            auto iter = hash.find(target-nums[i]);
            if(iter != hash.end())
            {
                v.push_back(i);
                v.push_back(iter->second);
                return v;
            }

            hash.insert(pair<int, int>(nums[i], i));
         }
         return v;
        
    }
};

运行结果如下：