InnoDB B+树索引

没有索引的查找

在一个页中的查找
假设目前表中的记录比较少，所有的记录都可以被存放到一个页中，在查找记录的时候可以根据搜索条件的不同分为两种情况：
1. 以主键为搜索条件
  这个查找过程我们已经很熟悉了，可以在页目录中使用二分法快速定位到对应的槽，然后再遍历该槽对应分组中的记录即可快速找到指定的记录。
2. 以其他列作为搜索条件
  对非主键列的查找的过程可就不这么幸运了，因为在数据页中并没有对非主键列建立所谓的页目录，所以我们无法通过二分法快速定位相应的槽。这种情况下只能从最小记录开始依次遍历单链表中的每条记录，然后对比每条记录是不是符合搜索条件。很显然，这种查找的效率是非常低的。
在很多页中查找
大部分情况下我们表中存放的记录都是非常多的，需要好多的数据页来存储这些记录。在很多页中查找记录的话可以分为两个步骤：
1. 定位到记录所在的页。
2. 从所在的页内中查找相应的记录。
在没有索引的情况下，不论是根据主键列或者其他列的值进行查找，由于我们并不能快速的定位到记录所在的页，所以只能从第一个页沿着双向链表一直往下找，在每一个页中根据我们刚刚介绍过的查找方式去查找指定的记录。因为要遍历所有的数据页，所以这种方式显然是超级耗时的，如果一个表有一亿条记录，使用这种方式去查找记录那要等到猴年马月才能等到查找结果。所以祖国和人民都在期盼一种能高效完成搜索的方法，索引同志就要亮相登台了。

一个简单的索引方案

mysql> CREATE TABLE index_demo(
    ->     c1 INT,
    ->     c2 INT,
    ->     c3 CHAR(1),
    ->     PRIMARY KEY(c1)
    -> ) ROW_FORMAT = Compact;
Query OK, 0 rows affected (0.03 sec)

回到正题，我们在根据某个搜索条件查找一些记录时为什么要遍历所有的数据页呢？因为各个页中的记录并没有规律，我们并不知道我们的搜索条件匹配哪些页中的记录，所以不得不依次遍历所有的数据页。所以如果我们想快速的定位到需要查找的记录在哪些数据页中该咋办？还记得我们为根据主键值快速定位一条记录在页中的位置而设立的页目录么？我们也可以想办法为快速定位记录所在的数据页而建立一个别的目录，建这个目录必须完成下面这些事儿：

下一个数据页中用户记录的主键值必须大于上一个页中用户记录的主键值。
给所有的页建立一个目录项。

InnoDB中的索引方案

设计InnoDB的大佬们需要一种可以灵活管理所有目录项的方式。他们灵光乍现，忽然发现这些目录项其实长得跟我们的用户记录差不多，只不过目录项中的两个列是主键和页号而已，所以他们复用了之前存储用户记录的数据页来存储目录项，为了和用户记录做一下区分，我们把这些用来表示目录项的记录称为目录项记录。

强调一遍目录项记录和普通的用户记录的不同点：

目录项记录的record_type值是1，而普通用户记录的record_type值是0。
目录项记录只有主键值和页的编号两个列，而普通的用户记录的列是用户自己定义的，可能包含很多列，另外还有InnoDB自己添加的隐藏列。
还记得我们之前在介绍记录头信息的时候说过一个叫min_rec_mask的属性么，只有在存储目录项记录的页中的主键值最小的目录项记录的min_rec_mask值为1，其他别的记录的min_rec_mask值都是0。

除了上述几点外，这两者就没什么差别了，它们用的是一样的数据页（页面类型都是0x45BF，这个属性在File Header中，忘了的话可以翻到前面的文章看），页的组成结构也是一样一样的（就是我们前面介绍过的7个部分），都会为主键值生成Page Directory（页目录），从而在按照主键值进行查找时可以使用二分法来加快查询速度。

想根据主键值查找一条用户记录大致需要3个步骤，以查找主键值为20的记录为例：

确定目录项记录页
我们现在的存储目录项记录的页有两个，即页30和页32，又因为页30表示的目录项的主键值的范围是[1, 320)，页32表示的目录项的主键值不小于320，所以主键值为20的记录对应的目录项记录在页30中。
通过目录项记录页确定用户记录真实所在的页。
在一个存储目录项记录的页中通过主键值定位一条目录项记录的方式说过了，不赘述了～
在真实存储用户记录的页中定位到具体的记录。
在一个存储用户记录的页中通过主键值定位一条用户记录的方式已经说过200遍了，你再不会我就，我就，我就求你到上一篇介绍数据页结构的文章中多看几遍，求你了～

那么问题来了，在这个查询步骤的第1步中我们需要定位存储目录项记录的页，但是这些页在存储空间中也可能不挨着，如果我们表中的数据非常多则会产生很多存储目录项记录的页，那我们怎么根据主键值快速定位一个存储目录项记录的页呢？其实也简单，为这些存储目录项记录的页再生成一个更高级的目录，就像是一个多级目录一样，大目录里嵌套小目录，小目录里才是实际的数据，所以现在各个页的示意图就是这样子：
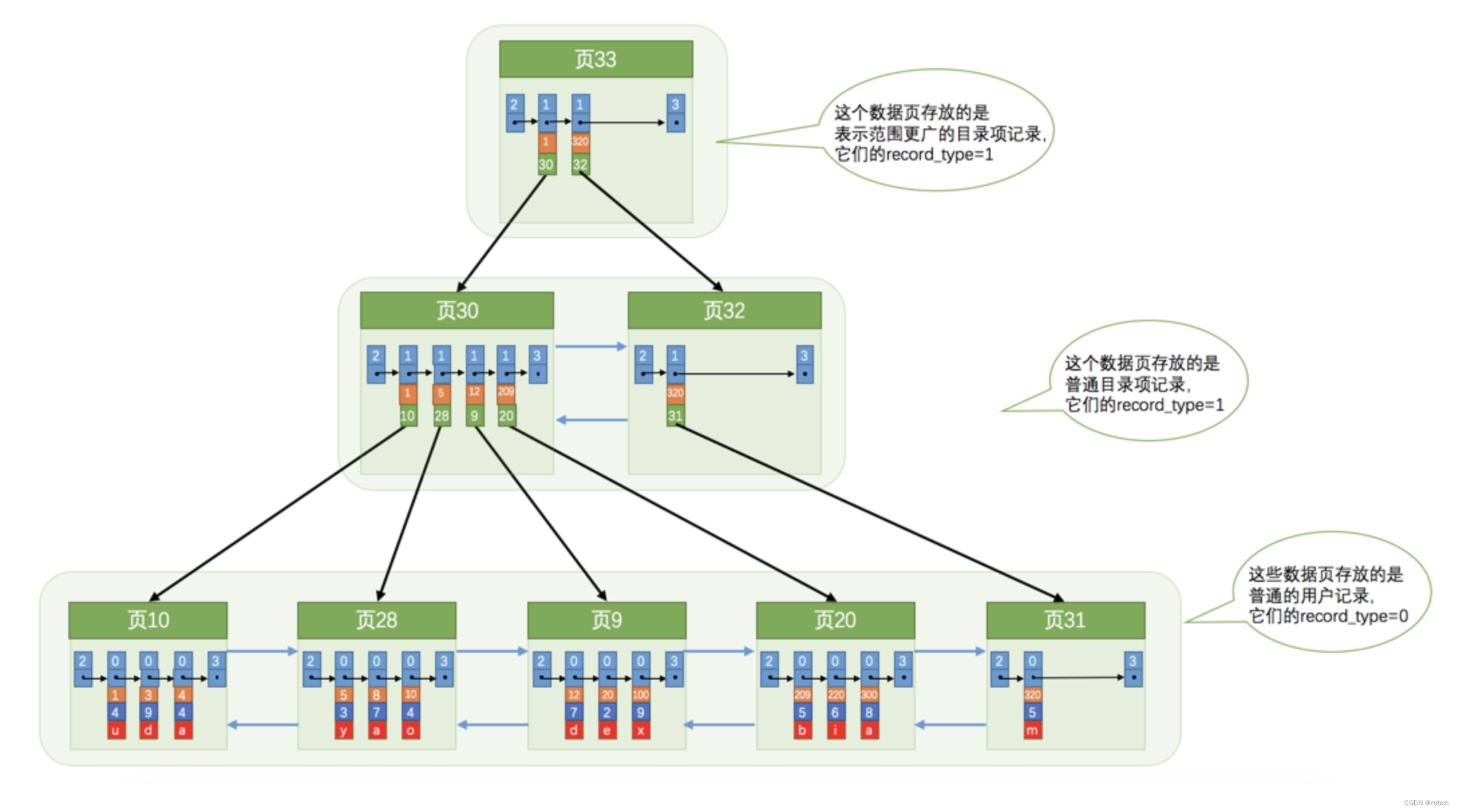
在这里插入图片描述

不论是存放用户记录的数据页，还是存放目录项记录的数据页，我们都把它们存放到B+树这个数据结构中了，所以我们也称这些数据页为节点。从图中可以看出来，我们的实际用户记录其实都存放在B+树的最底层的节点上，这些节点也被称为叶子节点或叶节点，其余用来存放目录项的节点称为非叶子节点或者内节点，其中B+树最上面的那个节点也称为根节点。

从图中可以看出来，一个B+树的节点其实可以分成好多层，设计InnoDB的大佬们为了讨论方便，规定最下面的那层，也就是存放我们用户记录的那层为第0层，之后依次往上加。之前的讨论我们做了一个非常极端的假设：存放用户记录的页最多存放3条记录，存放目录项记录的页最多存放4条记录。其实真实环境中一个页存放的记录数量是非常大的，假设，假设，假设所有存放用户记录的叶子节点代表的数据页可以存放100条用户记录，所有存放目录项记录的内节点代表的数据页可以存放1000条目录项记录，那么：

如果B+树只有1层，也就是只有1个用于存放用户记录的节点，最多能存放100条记录。

如果B+树有2层，最多能存放1000×100=100000条记录。

如果B+树有3层，最多能存放1000×1000×100=100000000条记录。

如果B+树有4层，最多能存放1000×1000×1000×100=100000000000条记录。哇咔咔～这么多的记录！！！

你的表里能存放100000000000条记录么？所以一般情况下，我们用到的B+树都不会超过4层，那我们通过主键值去查找某条记录最多只需要做4个页面内的查找（查找3个目录项页和一个用户记录页），又因为在每个页面内有所谓的Page Directory（页目录），所以在页面内也可以通过二分法实现快速定位记录。

聚簇索引

我们上面介绍的B+树本身就是一个目录，或者说本身就是一个索引。它有两个特点：

使用记录主键值的大小进行记录和页的排序，这包括三个方面的含义：
- 页内的记录是按照主键的大小顺序排成一个单向链表。
- 各个存放用户记录的页也是根据页中用户记录的主键大小顺序排成一个双向链表。
- 存放目录项记录的页分为不同的层次，在同一层次中的页也是根据页中目录项记录的主键大小顺序排成一个双向链表。
B+树的叶子节点存储的是完整的用户记录。
所谓完整的用户记录，就是指这个记录中存储了所有列的值（包括隐藏列）。

我们把具有这两种特性的B+树称为聚簇索引，所有完整的用户记录都存放在这个聚簇索引的叶子节点处。这种聚簇索引并不需要我们在MySQL语句中显式的使用INDEX语句去创建（后边会介绍索引相关的语句），InnoDB存储引擎会自动的为我们创建聚簇索引。另外有趣的一点是，在InnoDB存储引擎中，聚簇索引就是数据的存储方式（所有的用户记录都存储在了叶子节点），也就是所谓的索引即数据，数据即索引。

二级索引

大家有木有发现，上面介绍的聚簇索引只能在搜索条件是主键值时才能发挥作用，因为B+树中的数据都是按照主键进行排序的。那如果我们想以别的列作为搜索条件该咋办呢？难道只能从头到尾沿着链表依次遍历记录么？

不，我们可以多建几棵B+树，不同的B+树中的数据采用不同的排序规则。比方说我们用c2列的大小作为数据页、页中记录的排序规则，再建一棵B+树，效果如下图所示：

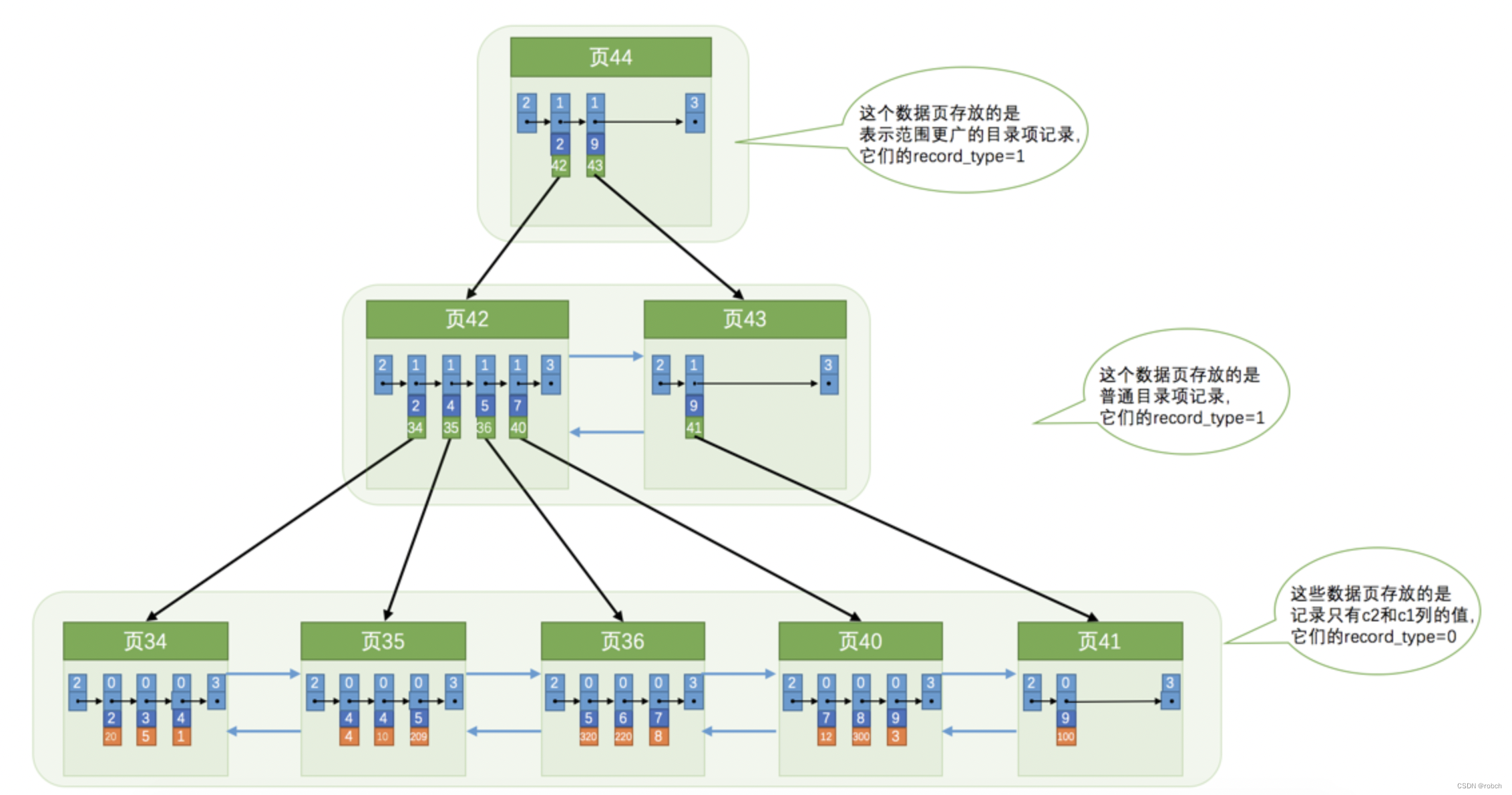
在这里插入图片描述
这个B+树与上面介绍的聚簇索引有几处不同：

使用记录c2列的大小进行记录和页的排序，这包括三个方面的含义：
- 页内的记录是按照c2列的大小顺序排成一个单向链表。
- 各个存放用户记录的页也是根据页中记录的c2列大小顺序排成一个双向链表。
- 存放目录项记录的页分为不同的层次，在同一层次中的页也是根据页中目录项记录的c2列大小顺序排成一个双向链表。
B+树的叶子节点存储的并不是完整的用户记录，而只是c2列+主键这两个列的值。
目录项记录中不再是主键+页号的搭配，而变成了c2列+页号的搭配。

我们根据这个以c2列大小排序的B+树只能确定我们要查找记录的主键值，所以如果我们想根据c2列的值查找到完整的用户记录的话，仍然需要到聚簇索引中再查一遍，这个过程也被称为回表。也就是根据c2列的值查询一条完整的用户记录需要使用到2棵B+树！！！

为什么我们还需要一次回表操作呢？直接把完整的用户记录放到叶子节点不就好了么？你说的对，如果把完整的用户记录放到叶子节点是可以不用回表，但是太占地方了呀～相当于每建立一棵B+树都需要把所有的用户记录再都拷贝一遍，这就有点太浪费存储空间了。因为这种按照非主键列建立的B+树需要一次回表操作才可以定位到完整的用户记录，所以这种B+树也被称为二级索引（英文名secondary index），或者辅助索引。由于我们使用的是c2列的大小作为B+树的排序规则，所以我们也称这个B+树为为c2列建立的索引。