目录
53.最大子数组和
134.加油站
968.监控二叉树
53.最大子数组和
53. 最大子数组和
中等
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组
是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1] 输出:1
示例 3:
输入:nums = [5,4,-1,7,8] 输出:23
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104
进阶:如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的 分治法 求解。
如果 -2 1 在一起,计算起点的时候,一定是从 1 开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
全局最优:选取最大“连续和”
局部最优的情况下,并记录最大的“连续和”,可以推出全局最优。
从代码角度上来讲:遍历 nums,从头开始用 count 累积,如果 count 一旦加上 nums[i]变为负数,那么就应该从 nums[i+1]开始从 0 累积 count 了,因为已经变为负数的 count,只会拖累总和。
class Solution {
// 求整数数组中的最大子数组和
public int maxSubArray(int[] nums) {
// 初始化结果变量为Integer的最小值,用于后续比较更新
int result = Integer.MIN_VALUE;
// sum用于累加当前子数组的和
int sum = 0;
// 遍历数组中的每个元素
for(int i = 0; i < nums.length; i++){
// 如果当前子数组的和为负数,则重新开始累加新的子数组(因为负数累加只会使和更小)
if(sum < 0){
sum = 0;
}
// 将当前元素加到sum上
sum += nums[i];
// 更新最大子数组和,如果sum大于result,则更新result
result = Math.max(result, sum);
}
// 返回最大子数组和
return result;
}
}暴力解法:
public class Solution {
public int maxSubArray(int[] nums) {
// 初始化结果变量result为整型的最小值,用于记录找到的最大子数组和
int result = Integer.MIN_VALUE;
// 初始化count变量为0,用于记录当前子数组的和
int count = 0;
// 外层循环,用于确定子数组的起始位置
for (int i = 0; i < nums.length; i++) {
// 每次进入外层循环时,将count重置为0,表示开始计算新的子数组的和
count = 0;
// 内层循环,用于确定子数组的结束位置
for (int j = i; j < nums.length; j++) {
// 将当前位置的元素加入count,即计算当前子数组的和
count += nums[j];
// 更新result的值,如果当前子数组的和count大于result,则更新result为count
result = Math.max(result, count);
}
}
// 返回找到的最大子数组和
return result;
}
}134.加油站
134. 加油站
中等
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2] 输出: 3 解释: 从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油 开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油 开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油 开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油 开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油 开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。 因此,3 可为起始索引。
示例 2:
输入: gas = [2,3,4], cost = [3,4,3] 输出: -1 解释: 你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。 我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油 开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油 开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油 你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。 因此,无论怎样,你都不可能绕环路行驶一周。
提示:
gas.length == ncost.length == n1 <= n <= 1050 <= gas[i], cost[i] <= 104
可以换一个思路,首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈,说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。
每个加油站的剩余量rest[i]为gas[i] - cost[i]。
i从0开始累加rest[i],和记为curSum,一旦curSum小于零,说明[0, i]区间都不能作为起始位置,因为这个区间选择任何一个位置作为起点,到i这里都会断油,那么起始位置从i+1算起,再从0计算curSum。
如图:
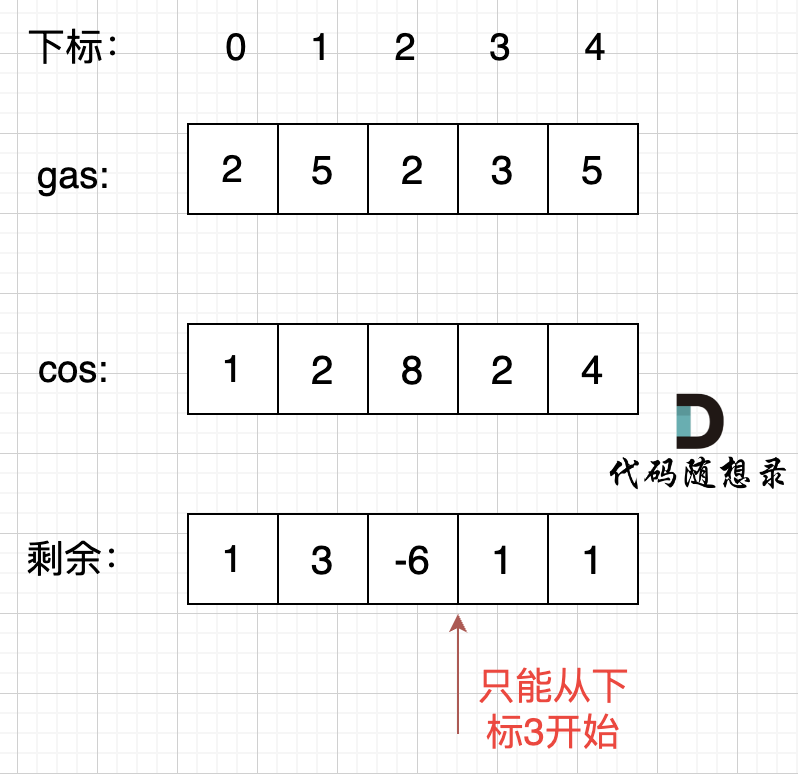
那么为什么一旦[0,i] 区间和为负数,起始位置就可以是i+1呢,i+1后面就不会出现更大的负数?
如果出现更大的负数,就是更新i,那么起始位置又变成新的i+1了。
那有没有可能 [0,i] 区间 选某一个作为起点,累加到 i这里 curSum是不会小于零呢? 如图:

如果 curSum<0 说明 区间和1 + 区间和2 < 0, 那么 假设从上图中的位置开始计数curSum不会小于0的话,就是 区间和2>0。
区间和1 + 区间和2 < 0 同时 区间和2>0,只能说明区间和1 < 0, 那么就会从假设的箭头初就开始从新选择其实位置了。
那么局部最优:当前累加rest[i]的和curSum一旦小于0,起始位置至少要是i+1,因为从i之前开始一定不行。全局最优:找到可以跑一圈的起始位置。
class Solution {
public int canCompleteCircuit(int[] gas, int[] cost) {
// 计算总的剩余油量,如果总剩余油量小于0,则无法完成一圈,直接返回-1
int totalSum = 0;
for(int i = 0; i < gas.length; i++){
totalSum += gas[i] - cost[i];
}
if(totalSum < 0){
return -1;
}
// curSum记录从start位置开始到当前位置的累计剩余油量
int curSum = 0;
// start记录可能的起始加油站位置
int start = 0;
// 遍历每个加油站,模拟汽车行驶一圈的过程
for(int i = 0; i < gas.length; i++){
// 加上当前加油站的油量,减去到达下一个加油站所需的油量
curSum += gas[i] - cost[i];
// 如果当前累计剩余油量小于0,说明从start位置出发无法到达当前加油站
// 因此将下一个加油站设为可能的起始位置,并将累计剩余油量重置为0
if(curSum < 0){
start = i + 1;
curSum = 0;
}
}
// 返回可能的起始加油站位置
return start;
}
}暴力解法:
public class Solution {
public int canCompleteCircuit(int[] gas, int[] cost) {
// 遍历每一个加油站作为起始点
for (int i = 0; i < cost.length; i++) {
int rest = gas[i] - cost[i]; // 记录从当前加油站出发后的剩余油量
int index = (i + 1) % cost.length; // 下一个要访问的加油站的索引,用取模运算实现循环
// 模拟从当前加油站出发,行驶一圈的过程
// 如果剩余油量大于0且没有回到起始点,则继续行驶
while (rest > 0 && index != i) {
rest += gas[index] - cost[index]; // 更新剩余油量,加上下一个加油站的油量,减去到下一个加油站所需的油量
index = (index + 1) % cost.length; // 移动到下一个加油站
}
// 如果行驶完一圈后剩余油量大于等于0,并且回到了起始点,说明从当前加油站出发可以完成一圈
if (rest >= 0 && index == i) return i; // 返回起始加油站的索引
}
// 如果遍历完所有加油站都没有找到可以完成一圈的起始点,则返回-1
return -1;
}
}968.监控二叉树
968. 监控二叉树
困难
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:

输入:[0,0,null,0,0] 输出:1 解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
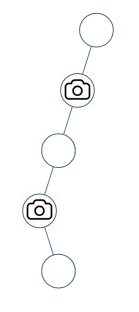
输入:[0,0,null,0,null,0,null,null,0] 输出:2 解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
- 给定树的节点数的范围是
[1, 1000]。 - 每个节点的值都是 0。
直接看代码很容易看懂
class Solution {
// 全局变量,记录最终需要放置的摄像头数量
int res = 0;
// 主函数,返回需要放置的摄像头数量
public int minCameraCover(TreeNode root) {
// 对根节点的状态进行检验,防止根节点处于无覆盖状态
if (minCame(root) == 0) {
// 如果根节点处于无覆盖状态,则需要在其父节点(这里假设为根节点的外部)放置一个摄像头
res++;
}
return res;
}
/**
* 递归函数,用于计算节点状态并返回状态值
* 节点状态值定义:
* 0 - 表示无覆盖
* 1 - 表示有摄像头
* 2 - 表示有覆盖
* 使用后序遍历,根据左右子节点的状态,判断当前节点的状态
*/
public int minCame(TreeNode root) {
if (root == null) {
// 空节点默认处于有覆盖状态,避免在叶子节点上放置摄像头
return 2;
}
// 递归计算左子节点和右子节点的状态
int left = minCame(root.left);
int right = minCame(root.right);
// 根据左右子节点的状态判断当前节点的状态
if (left == 2 && right == 2) {
// 如果左右子节点都处于有覆盖状态,则当前节点处于无覆盖状态
// 此时,如果根节点处于无覆盖状态,那么根节点的父节点需要放置摄像头
return 0;
} else if (left == 0 || right == 0) {
// 如果左右子节点中至少有一个处于无覆盖状态,则当前节点需要放置摄像头
// 摄像头数量增加
res++;
// 当前节点有摄像头,返回状态值1
return 1;
} else {
// 左右子节点至少有一个摄像头,则当前节点处于有覆盖状态
// 返回状态值2
return 2;
}
}
}代码随想录 (programmercarl.com)