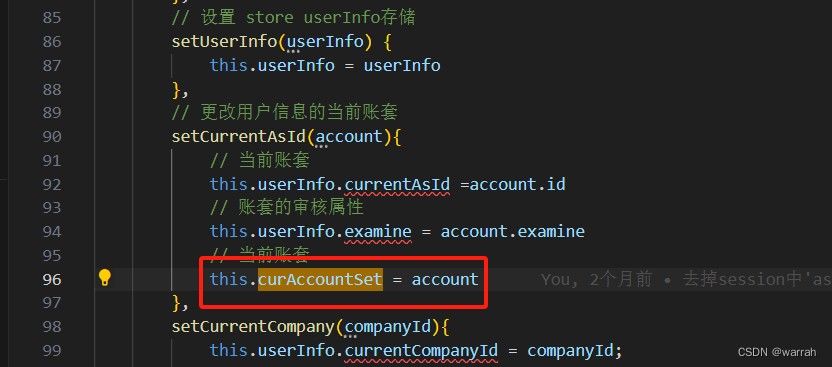
solution1(通过60%)

观察数据发现,最大公约数为abs(a-b)
当abs(a-b) => min(a, b)时，最小增量为g - min(a, b)

#include<iostream>
#include<algorithm>

typedef long long LL;

using namespace std;
int main(){
	LL a, b, g, k = -1, t1, t2;
	scanf("%lld%lld", &a, &b);
	g = abs(a - b);
	if(g >= min(a, b)){
		k = g - min(a, b);
	}
	else{
		for(LL i = 1; i < 1e6; i++){
			t1 = (a + i) % g;
			t2 = (b + i) % g;
			if(t1 == 0 && t2 == 0){
				k = i;
				break;
			}
		}
	}
	printf("%lld", k);
	return 0;
}

solution2

gcd(a, b) = gcd(a, b - a)
=>gcd(a + k, b + k) = gcd(a + k, b - a)
若a >= b，则找到gcd(a + k, a - b)最大为a - b
问题转化为找到满足(a+k)%(a-b)==0的最小k
记g = a - b，则(a + k) % g = (a %g + k % g)%g
a%g < g, k %g < g，则g - a%g = = k

#include<iostream>
#include<algorithm>

typedef long long LL;

using namespace std;
int main(){
	LL a, b;
	scanf("%lld%lld", &a, &b);
	if(a < b) swap(a, b);
	printf("%lld", (a -b) - a % (a - b));
	return 0;
}