C++ 图进阶系列之纵横对比 Bellman-Ford 和 Dijkstra 最短路径求解算法

news2024/11/30 14:49:16

1. 前言

因无向、无加权图的任意顶点之间的最短路径由顶点之间的边数决定，可以直接使用原始定义的广度优先搜索算法查找。

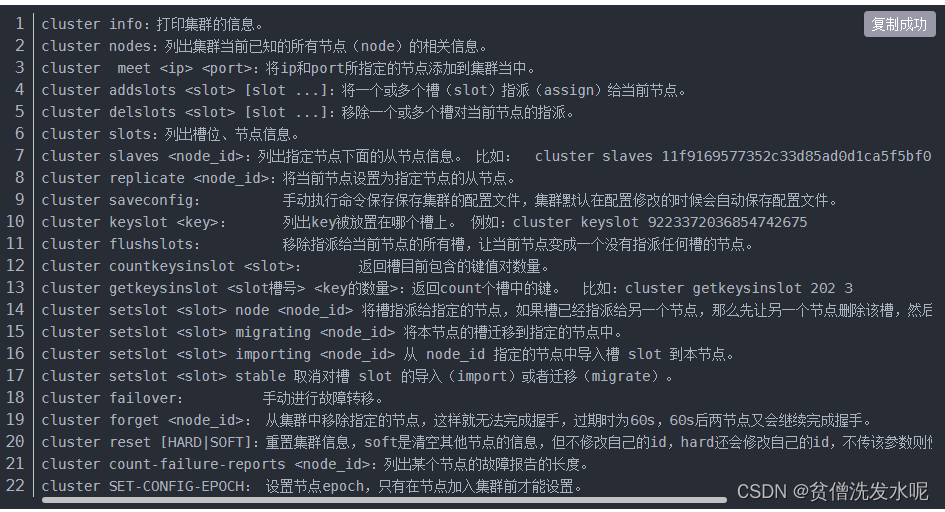
但是，无论是有向、还是无向，只要是加权图，最短路径长度的定义是：起点到终点之间所有路径中权重总和最小的那条路径。

如下图所示，A 到 C 的最短路径并不是A直接到 C（权重是 9），而是 A 到 B 再到 C（权重是 7）。所以，需要在广度优先搜索算法的基础上进行算法升级后才能查找到。

DJ01.png

加权图的常用最短路径查找算法有：

  • 贝尔曼-福特（Bellman-Ford）算法。
  • Dijkstra（迪杰斯特拉） 算法。
  • A* 算法。
  • D* 算法。

本文重点介绍 Bellman-Ford和Dijkstra算法。

2. 贝尔曼-福特（Bellman-Ford）算法

贝尔曼-福特算法取自于创始人理查德.贝尔曼和莱斯特.福特，本文简称 BF 算法

BF 算法属于迭代、穷举算法，算法效率较低，如果图结构中顶点数量为 n，边数为 m ，则该算法的时间复杂度为 m*n ，还是挺大的。

理论上讲，图结构中边上的权重一般用来描述现实世界中的速度、时间、花费、里程……基本上都是非负数。即使是负数，BF 算法也能工作得较好。

2.1 BF 算法思想

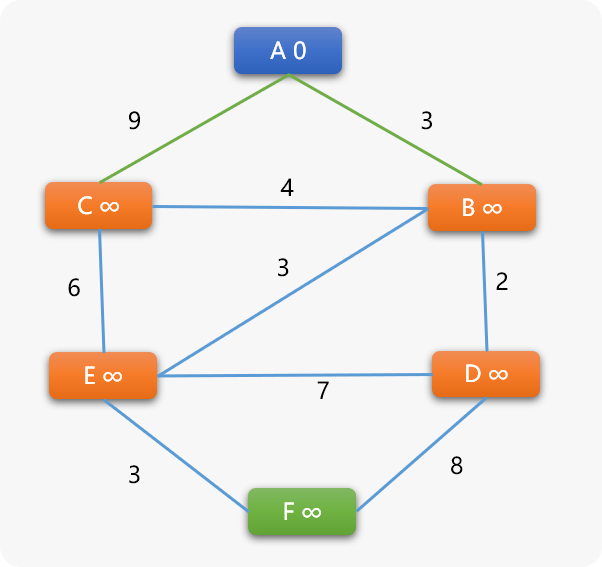
问题描述：如下图，搜索 A 到其它任意顶点之间的最短路径。

首先给每一个顶点一个权重值（用来存储从起始顶点到此顶点的最短路径上所有边上权重之和），刚开始除了出发点的权重 0 ，因为还不能确定到其它任意顶点的具体路径长度，其它顶点的权重值均初始为无穷大（只要是一个适当值都可以）。

下面的图结构是无向加权图，对于有向加权图同样适用 BF 算法。

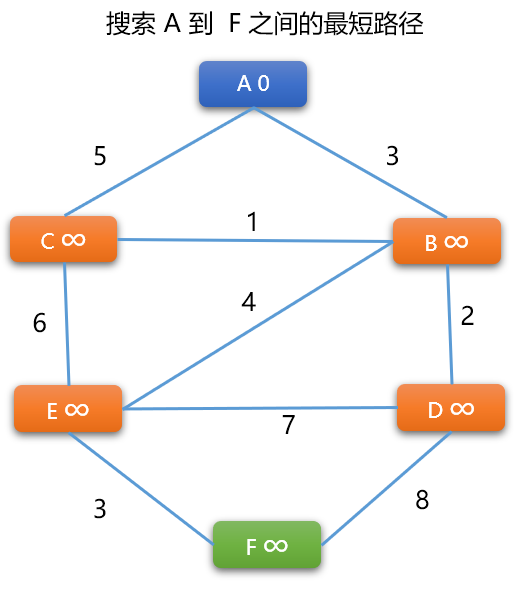
BF01.png

BF 算法流程

更新顶点的权重： 计算任一条边上一端顶点（始点）到另一个端顶点（终点）的权重。新权重=顶点（始点）权重+边的权重，然后使用新权重值更新终点的原来权重值。

更新原则： 只有当顶点原来的权重大于新权重时，才更新。

  • 先选择 A -> B 之间的路径，因为 A~B 是无向边，需要计算 2 次。如果是有向图，则只计算一个方向。

    先计算 A -> B 的新权重=A的权重+（A，B）边上的权重，新权重=0+3=3。因 3 小于 B 顶点现在的权重（无穷大），B 的权重被更新为 3。

    再计算 B -> A 的新权重=B的权重+(A，B) 边上的权重。新权重=3+3=6。6 大于 A 现有的权重 0，则 A 顶点不更新。

Tips： 此时，意味着 A -> B 的最短路径长度为 3。A 是 B 的前序顶点。 但是，这绝对不是最后的结论。

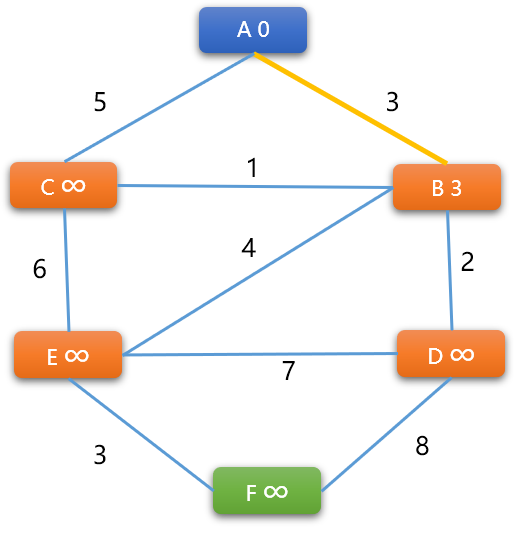
BF02.png

  • 对图中每一条边两端的顶点都执行上述同样的操作，对于执行顺序没有特定要求。如下继续计算 （A，C） 边的两端顶点的权重。

    A -> C 的新权重=0+5=5，更新 C 顶点权重为 5。

    C -> A 的新权重=5+5=10 不更新。结论：A 是 C 的前序顶点。

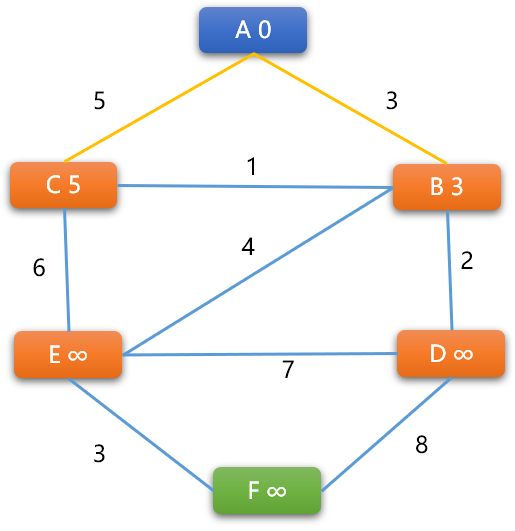
BF03.png

  • 计算 （B，C） 权重：

    B -> C 的新权重=3+1=4，小于 C 现有权重 5 ，C 的权重更新为 4，则 B 是 C的前序顶点

    C -> B 的新权重= 4+1 =5 ，大于 B 现有权重，不更新。

    经过上述操作后 （A，B，C）3 个顶点的前序关系：A 是 B 的前序、B 是 C 的前序，当前 A -> B 的最短路径是 3，A -> B -> C 的最短路径是 4，但不一定是最后结论。

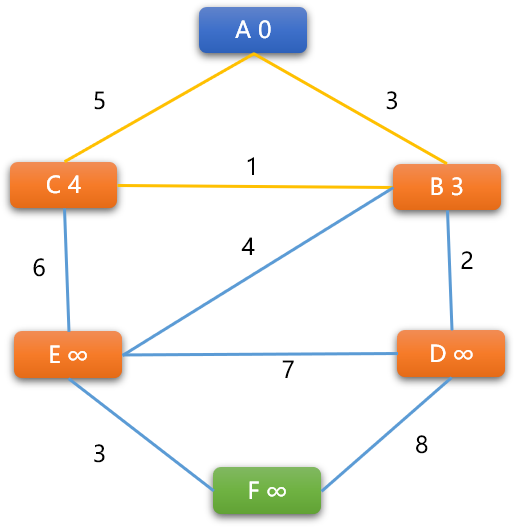
BF04.png

Tips： 当顶点的权重更新后，也意味着前序顶点也发生了变化。如上述权重更新过程中 C 刚开始前序是 A，后来又更改成了 B。

  • 当所有边两端顶点都更新完毕后，需要再重新开始，对图结构中所有边上的顶点权重再进行一次更新，一直到不再引起权重变化时 BF 算法才算结束。

  • BF 算法的本质还是广度优先搜索算法，附加了更新顶点权重的逻辑。

2.2 结构设计

在实现算法之前，先要为图设计一系列类型。

2.2.1 顶点类型

此类用来描述顶点本身信息，除了有顶点的常规属性，如编号、名称、链接表……外，还需要添加 2 个属性：

  • 顶点的权重： 初始化时为无穷大。

    Tips: 顶点权重用来保存起始点到此顶点的最短路径长度（边上权重之和）。

  • 前序顶点： 在 BF 算法中，如果顶点的权重发生了更新，也意味着前序顶点也发生了变化。

基本结构：

#include <iostream>
#include <map>
#include <climits>
#include <vector>
#include <queue>
using namespace std;
/*
* 结（顶）点类
*/
template<typename T>
struct Vertex {
	//顶点的编号
	int vId;
	//顶点所承载的值
	T value;
	//是否被访问过:False 没有 True:有
	bool visited;
	//与此顶点相连接的其它顶点
	map< Vertex<T>*,int > connectedTo;
	//前序顶点
	Vertex<T>* preorderVertex;
	// 权重（初始为无穷大）,为了研究方便，此处权重为 int  类型
	int weight = INT_MAX;
	//无参构造函数
	Vertex() {
		this->visited=false;
		this->vId=-1;
		this->preorderVertex=NULL;
	}
	//有参构造函数
	Vertex(int  id,T value) {
		this->vId=id;
		this->value=value;
		this->visited=false;
		this->preorderVertex=NULL;
	}

继续在顶点结构体中添加如下的函数，满足对顶点的一系操作。

添加相邻顶点函数

/*
*添加邻接顶点
*nbrVer:相邻顶点
*weight:无向无权重图，权重默认设置为 1
*/
void addNeighbor(Vertex<T>* nbrVer,int weight=1) {
    //map 中以相邻顶点为键，边权重为值
    this->connectedTo[nbrVer]=weight;
}

/*
*判断给定的顶点是不是当前顶点的相邻顶点
*/
bool isNeighbor( Vertex<T>* nbrVer) {
    //检查
    typename::std::map< Vertex<T>,int >::iterator iter= this->connectedTo.find(nbrVer) ;
    if( iter==this->connectedTo.end() )return false;
    return true;
}

顶点对象以字符串格式输出

/*
*显示当前顶点以及与之相邻的其它顶点
*/
void desc() {
    cout<<"顶点编号:"<<this->vId<<";顶点值:"<<this->value<<"顶点权重："<<this->weight<<endl;
    int count= this->connectedTo.size();
    cout<<"相邻顶点："<<count;
    typename::std::map< Vertex<T>*,int >::iterator begin= this->connectedTo.begin();
    typename::std::map< Vertex<T>*,int >::iterator end= this->connectedTo.end();
    while(begin!=end) {
        //（编号，值，边权重）
        cout<<"\t("<<begin->first->vId <<","<<begin->first->value<<","<<begin->second<<")"<<"\t";
        begin++;
    }
    cout<<endl;
}

更新顶点权重函数

此函数为 BF 算法的核心子逻辑，参数 nbrVer 是指与当前顶点相邻的顶点。先是计算和当前顶点的新权重，根据更新原则进行更新。如果有更新则需要把当前顶点指定为前序顶点。

/*
*得到和某一个相邻顶点的权重
*/
int getWeight(Vertex<T>* nbrVer) {
    return this->connectedTo[nbrVer];
}

/*
*计算顶点权重（路径长度）
*/
bool  calBfWeight(Vertex<T>* nbrVer) {
    // 顶点权重加上顶点间边的权重
    int newWeight = this->weight + this->getWeight(nbrVer);

    if (newWeight < nbrVer->weight) {
        // 计算出来权重小于顶点原来权重，则更新
        nbrVer->weight=newWeight;
        // 更新前序顶点
        nbrVer->preorderVertex = this;
        return 1;
    }
    return 0;
}

Tips： 在图结构中，最短路径算法中的前序顶点指到达此顶点最近的顶点。

重载函数

//重载 < 运算符
bool operator<(const Vertex<T> & vert) const {
    return  this->vId<vert.vId;
}
//重载 == 运算符
bool operator==(const Vertex<T> & vert) const {
    return  this->vId==vert.vId;
}

2.2.2 图类

此类用来对图中的顶点进行维护，如添加新顶点，维护顶点之间的关系、提供BF 搜索算法……

图类的基本结构

template<typename T>
class Graph {
    private:
        // 一维列表，存储所有结点
        vector< Vertex<T>* > vertList;
        // 顶点个数
        int vNums = 0;
        // 队列，用于路径搜索算法
        queue<Vertex<T>* > pathQueue;
        //保存任意顶点之间的最短路径
        vector< vector< Vertex<T>* > > allPath;
    public:
    /*
	*无参构造函数
	*/
    Graph() {}
    //其它

其它功能函数

  • 查询函数: 有 2 个，一个按值在图中查询单个顶点，一个在图中查询所有顶点。
/*
*按值查询顶点是否存在
*/
Vertex<T>* findVert(T  vertValue) {
    for(int i=0; i<this->vNums; i++) {
        if( this->vertList[i]->value==vertValue )
            return this->vertList[i];
    }
    return NULL;
}

/*
*查询所有顶点
*/
void findVertexes() {
    for(int i=0; i<this->vNums; i++) {
        this->vertList[i]->desc();
    }
}
  • 添加新顶点以及维护顶点之间的关系函数： 新顶点的编号由内部提供，统一管理，保证编号的一致性。
/*
* 添加新顶点
*/
Vertex<T>* addVertex( T  vertValue) {
    //检查顶点是否存在
    Vertex<T>* vert=this->findVert(vertValue);
    if(vert!=NULL )return vert;
    // 顶点的编号内部生成
    vert=new Vertex<T>(this->vNums, vertValue);
    // 存储顶点
    this->vertList.push_back(vert);
    // 计数
    this->vNums++;
    return vert;
}

/*
* 添加顶点与顶点之间的关系（边），
* 如果是无权重图，统一设定为 1
*/
void addEdge(T fromValue,T toValue,int weight=1) {
    // from节点
    Vertex<T>* fromVert=this->addVertex(fromValue);
    //to 结点
    Vertex<T>* toVert=this->addVertex(toValue);
    //调用顶点自身的添加相邻顶点方法。
    fromVert->addNeighbor(toVert,weight);
}
  • 贝尔曼-福特算法： 这里用到了递归，在 BF 算法中，一轮更新后可能还需要后续多轮更新才能让每一个顶点上的权重不再变化。这也是 BF 算法的缺陷。
/*
*贝尔曼-福特算法
*/
void bfNearestPath(Vertex<T> *from_v) {
    Vertex<T>* tmp_v;
    from_v->weight=0;
    // 记录边更新次数
    int update_count = 0;
    // 起始点压入队列
    this->pathQueue.push(from_v);
    // 检查队列是否为空
    while(!this->pathQueue.empty()) {
        //从队列获取顶点
        tmp_v = this->pathQueue.front();
        this->pathQueue.pop();
        // 标记为已经处理
        tmp_v->visited = true;
        // 得到与其相邻顶点
        map< Vertex<T>*,int > nbr_vs = tmp_v->connectedTo;
        
        typename::std::map< Vertex<T>*,int >::iterator begin=nbr_vs.begin();
        typename::std::map< Vertex<T>*,int >::iterator end=nbr_vs.end();

        // 更新与其相邻顶点的权重
        while(begin!=end) {
            Vertex<T>* v_=begin->first;
            // 更新权重，并记录更新次数
            update_count += tmp_v->calBfWeight(v_);
            // 无向边，要双向更新
            update_count +=v_->calBfWeight(tmp_v);
            // 把相邻顶点压入队列
            if (!v_->visited) {
                this->pathQueue.push(v_);
                v_->visited=true;
            }
            begin++;
        }
    }
    // 更新完毕后，如果更新次数为 0 ，则不用再更新。
    if (update_count != 0) {
        this->bfNearestPath(from_v);
    }
}
  • 输出最短路径函数： 先计算，再输出。
/*
*显示任意 2 个顶点之间的最短路径
*/
void getAllPath(T  value ) {
    //起始结点
    Vertex<T>*  startv= this->findVert(value);
    for(int i=0; i<this->vNums; i++ ) {
        Vertex<T>*  t_v = this->vertList[i];
        if(t_v==startv)continue;
        vector<Vertex<T>*  > path;
        path.push_back(t_v);
        while (1) {
            // 找到前序顶点
            Vertex<T>* pv= t_v->preorderVertex;
            path.push_back(pv);
            if(pv==startv) {
                this->allPath.push_back(path);
                break;
            }
            t_v=pv;
        }
    }
}

void showAllPath( T  value ) {
    cout<<"(----------f_v~t_v 最短路径长度------------)"<<endl;
    for(int i=0; i<this->allPath.size(); i++  ) {
        //起始结点
        Vertex<T>*  startv= this->findVert(value);
        //输出起始点
        cout<<startv->value<<"("<<startv->weight<<")"<<"->";
        int weight=0;
        for(int j=this->allPath[i].size()-1; j>=0; j-- ) {
            //
            Vertex<T>* tmp=this->allPath[i][j];
            //如果是起始点
            if(tmp==startv)continue;
            //得到相邻顶点的权重
            weight+=startv->getWeight(tmp);
            startv=tmp;
            cout<<startv->value<<"("<<startv->weight<<")"<<"->";
        }
        cout<<"最短路径的值"<<weight<<endl;
    }
}

测试图类中的函数：

  • 添加顶点以及顶点之间的关系：
int main(int argc, char** argv) {
	// 初始化图
	Graph<char> graph;
	// 添加节点
	char verts[]= {'A', 'B', 'C', 'D', 'E', 'F'};
	for(int i=0; i<sizeof(verts); i++ ) {
		graph.addVertex(verts[i]);
	}

	// 添加顶点之间关系
	char v_to_v[9][3] = { {'A', 'B', 3},  {'A', 'C', 5} , {'B', 'C', 1 } , { 'B', 'D', 2 } , {'B', 'E', 4} , { 'C', 'E', 6}, {'D', 'E', 7},
		{'D', 'F', 8},
		{'E', 'F', 3}
	};

	for(int i=0; i<9; i++) {
		graph.addEdge( v_to_v[i][0], v_to_v[i][1], v_to_v[i][2] );
		graph.addEdge( v_to_v[i][1], v_to_v[i][0], v_to_v[i][2] );
	}
    //显示图中的所有顶点以及顶点之间的关系
	graph.findVertexes();
	return 0;
}

测试结果：

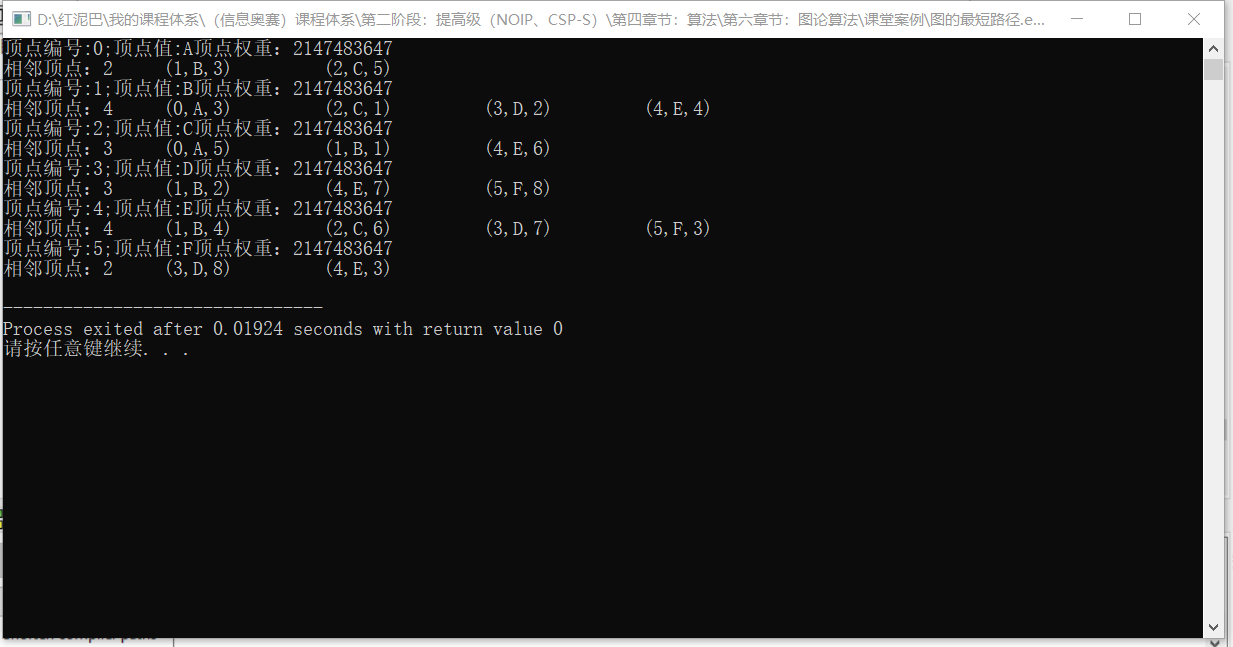
BF06.png

  • BF算法测试
int main(int argc, char** argv) {
	//省略……
	//查找任一顶点到 'A' 顶点之间的最短路径长度
	Vertex<char>* fromV=   graph.findVert('A');
    //BF 算法
	graph.bfNearestPath(fromV);
	cout<<"---------BF后顶点的权重----------"<<endl;
	graph.findVertexes();
	graph.getAllPath('A');
	graph.showAllPath('A');
	return 0;
}

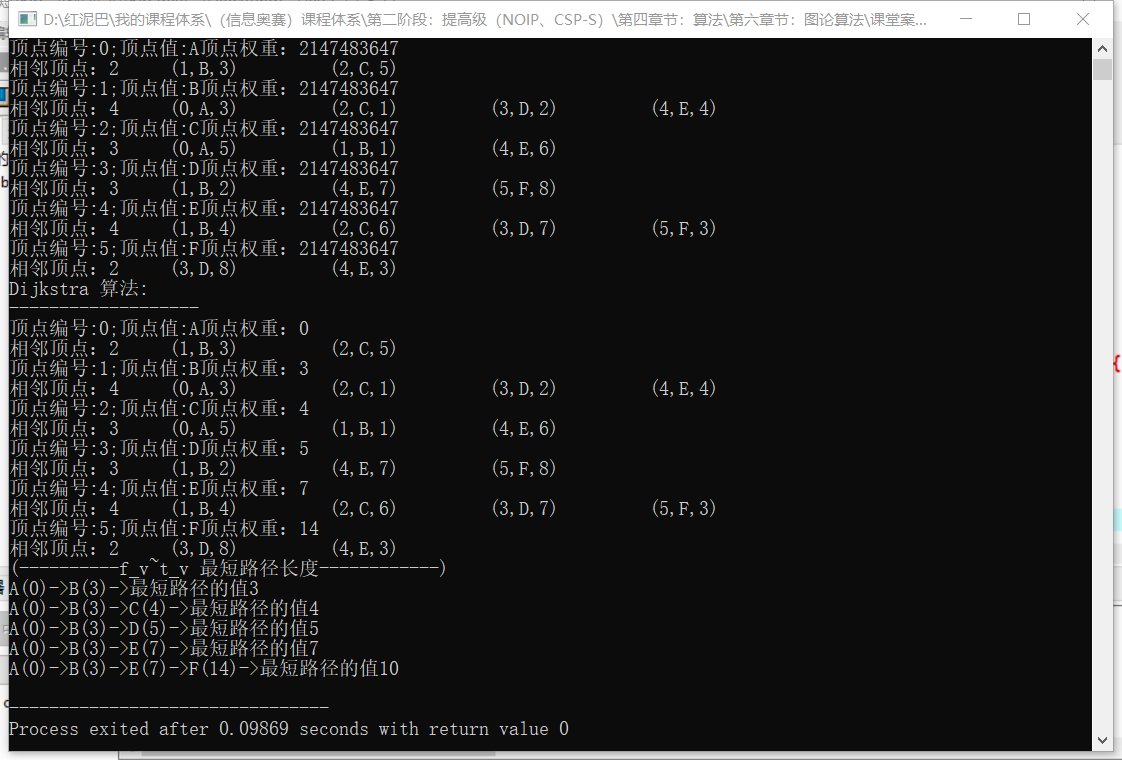
输出结果：

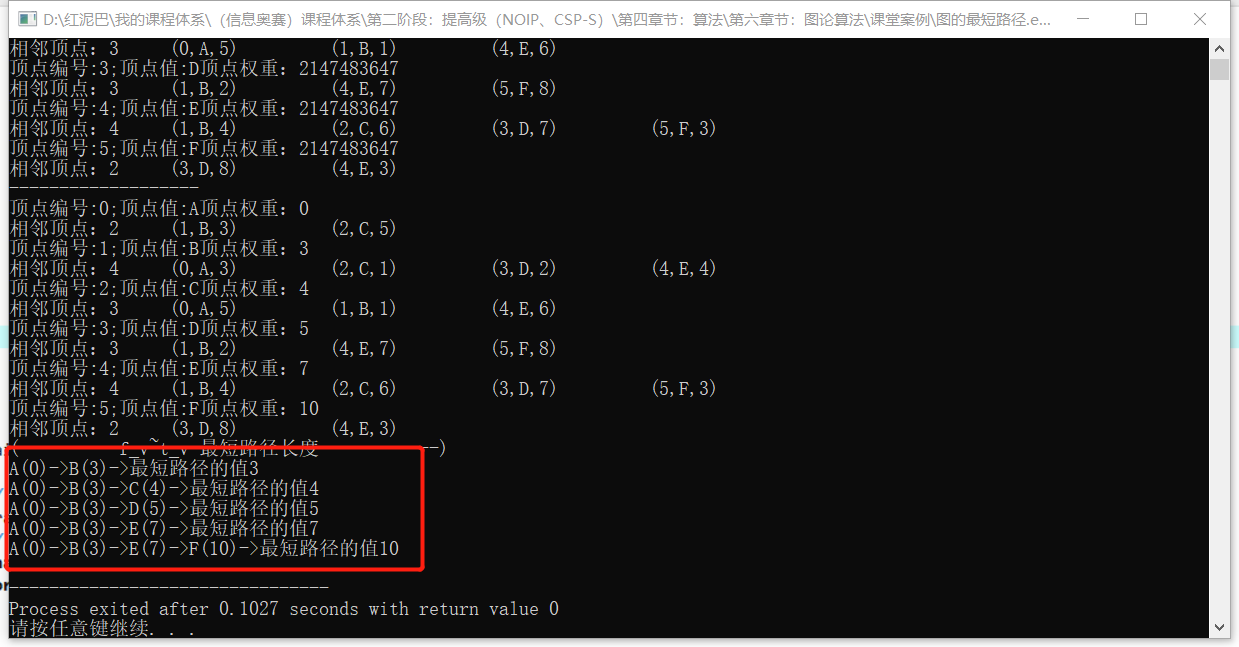
BF07.png

如下图，路径中最后一个顶点的权重就是起点A到此顶点的最短路径值(路径权重)。

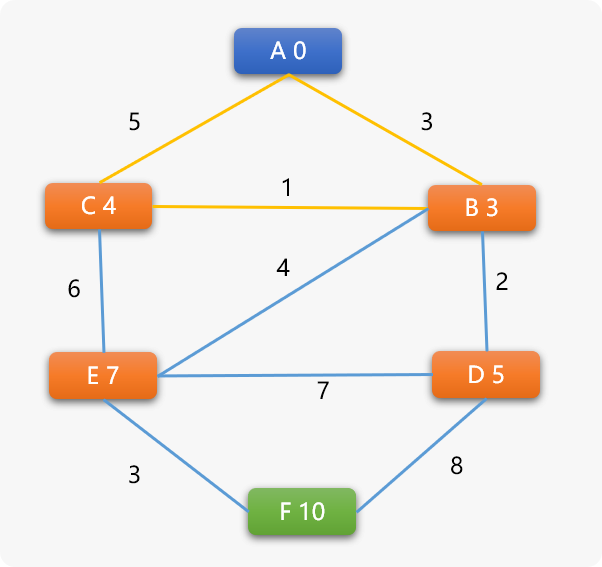
BF05.png

3. Dijkstra（迪杰斯特拉）算法

迪杰斯特拉算法(Diikstra) 是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。为了便于表述，本文简称 DJ 算法。

DJ 算法和前面所聊的 BF 算法，可谓同工异曲，算法的核心思想是相同的：

  • 搜索到某一个顶点后，更新与其相邻顶点的权重。

    Tips： 权重计算法则以及权重更新原则两者相同。

  • 且顶点权重的数据含义和 BF 算法的一样。表示从起始点到此点的最短路径长度（也就是经过的所有边的权重之和）。

    Tips： 初始时，因还不能具体最短路径，起始点的权重为 0 ，其它顶点权重可设置为无穷大。

DJ 算法相比较 BF 算法有 2 个不同的地方：

  • 在无向加权图中，BF 算法需要对相邻 2 个顶点进行双向权重计算。
  • DJ 算法搜索时，每次选择的下一个顶点是所有权重值最小的顶点。**其思想是保证每一次选择的顶点和当前顶点权重都是最短的。**所以，DJ是基于贪心思想。

3.1 DJ 算法流程

如下图结构中，查找 A 到任一顶点的最短路径：

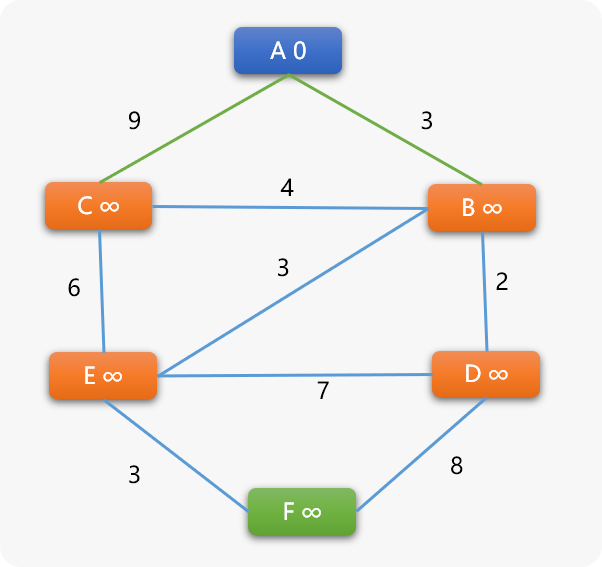
DJ01.png

  1. 定位到起始点 A ， A 顶点也称为当前顶点。

  • 设置 A 的权重为 0，A 的相邻顶点有 B 和 C，需要计算 A 到 B 以及 A 到 C 之间的权重。这里是先选择 B 还是 C 并不重要。先选择 B 顶点，计算 A -> B 的路径长度权重。新权重计算公式＝A顶点权重＋（A，B）边的权重＝０＋３＝３．

  • 更新原则和 BF 算法一样，当计算出来的权重值小于相邻顶点的权重值时，更新。于是 B 的权重更新为 ３．此时 A 是 B 的前序顶点。

  • 再选择 C 顶点，计算 A -> C 路径长度权重＝０＋9＝9，因 9 小于 C 现在的无穷大权重，C 的权重被更新为 9。

Tips： 到这里， 可以说 DJ 算法和 BF 算法没有什么不一样。

但是，DJ 算法不需要对边上 2 个顶点进行双向权重计算，这是 DJ 算法与 BF 算法的第一个差异性。

此时，更新后的图结构如下所示:

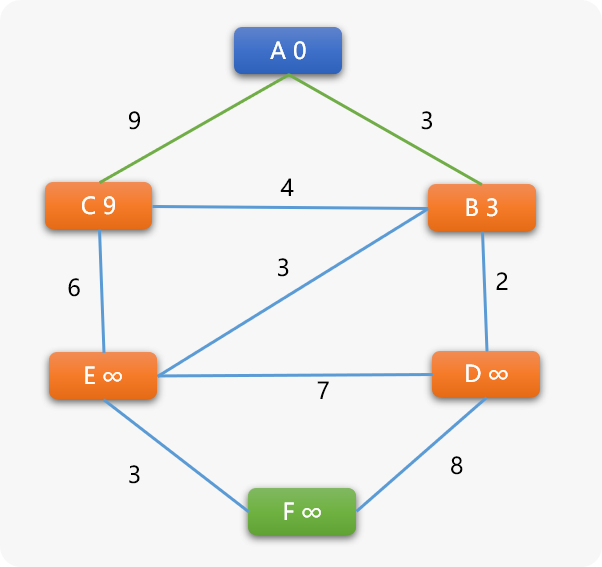
DJ02.png

很显然， B 和 C 将成为下一个搜索的候选点，这里 DJ 算法和 BF 算法就有了很大的差异性。

BF 算法对于选择 B 还是 C 的顺序没有要求。

DJ 算法则不同，会选择 B 和 C 中权重值更小的那个， B 的权重 3 小于 C 的权重 9 ，当然选择 B 为下一个搜索顶点。

这是 BF 算法和 DJ 算法的第二个差异性！

选择 B 后也就意味着 A->B 之间的最短路径就确定了。为什么？

因你无法再找出一条比之更短的路径。

这里也是 DJ 算法的关键思想，在选择一个权重最小的候选顶点后，就能确定此顶点和它的前序顶点之间的最短路径长度。

Tips： 到现在为止， B 的前序顶点是 A；C 的前序顶点也是 A 。

因为 B 已经被选为下一个搜索顶点，于是 B 顶点和它的前序顶点 A 之间的最短路径已经出来了。

A－＞Ｂ　最短路径长度为 ３。

因 C 顶点还没有成为搜索顶点，其和 A 顶点之间的最短路径还是一个未知数。

  1. Ｂ成为当前顶点

  • 找到与 B 相邻的 C、D、E 3 个顶点，然后分别计算路径长度权重。B->C 的新权重=３+4＝７ 小于 C 现有的权重 ９ ，C 的权重被更新为 ７ ，C 的前序顶点也变成了 B。

    同理，B->D 路径中 D 的权重被更新为 5；B->E 路径中 E 的权重被更新为 ６ 。

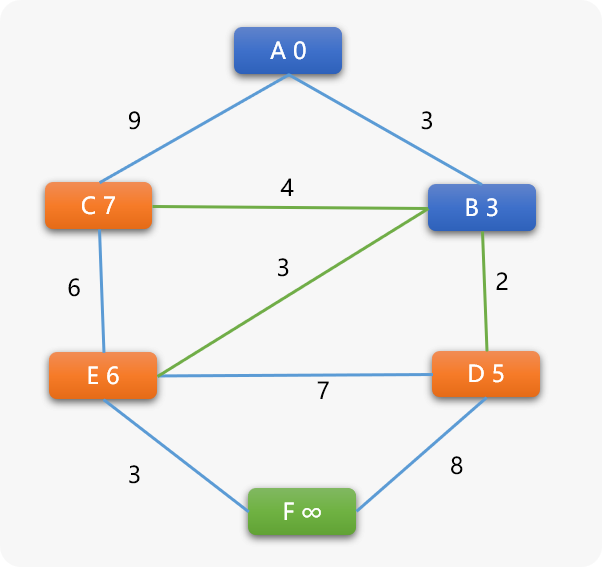
DJ03.png

  • 再在 C、 D、 E 3 个顶点中选择权重值最小的 D 为下一个搜索顶点．到这里！可以发现 DJ 算法和原始定义的广度搜索算法以及 BF 之间就有了本质上的区别：

    广度优先搜索算法会选择和 B 同时进入队列的 C 顶点成为下一个搜索顶点。因为 B 和 C 都是离 A 较近的顶点。

    而 DJ 算法是在候选顶点中，哪一个顶点的权重最少，就选择谁，不采用就近原则．而是以顶点的权重值小作为优先选择条件．

Tips： 选择 D 后 ，各顶点间的关系：

B 的前序是 A，（Ａ，Ｂ）间最短路径已经确定。

D 的前序是 B ，（Ｂ，Ｄ）间的最短路径可以确定，又因为 B 的前序顶点是 A ，所以 A－＞B－＞D 的最短路径可以确定。

其它项点间的最短路径暂时还不明朗。

  1. D 顶点为当前顶点

  • 计算与 D 相邻的 E、F 顶点的权重。

    D->E 的新权重=5+7=12 大于 E 现有权重 6 ，不更新。E 的前序顶点还是 B。

    D->F 的新权重=5+8=13 ，F 的权重由无穷大更新为 13。

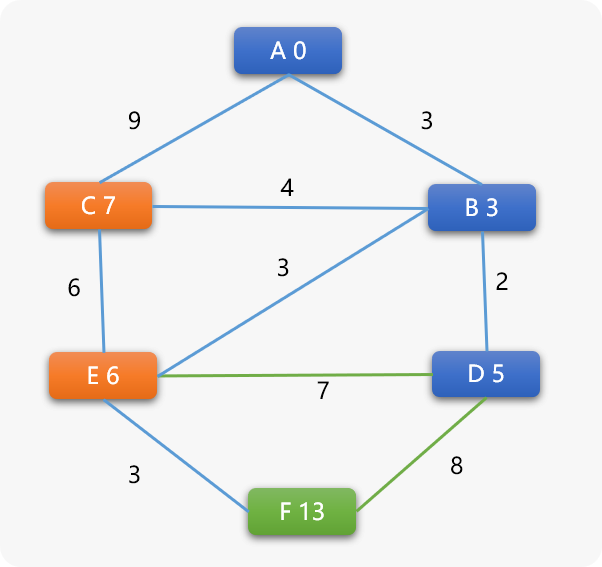
DJ04.png

  • 再在剩下的所有可选顶点中选择权重值小的 E 顶点为下一个搜索点，当选择 E 后：

Tips： E 的前序为 B , B 的前序是 A，所以 A 到 E 的最短路径长度就是 A->B->C ，路径长度为 6。

  1. E 为当前顶点，计算和其相邻顶点间的权重。

唯一可改变的是 F 顶点的权重，F 顶点的前序顶点变为 E。

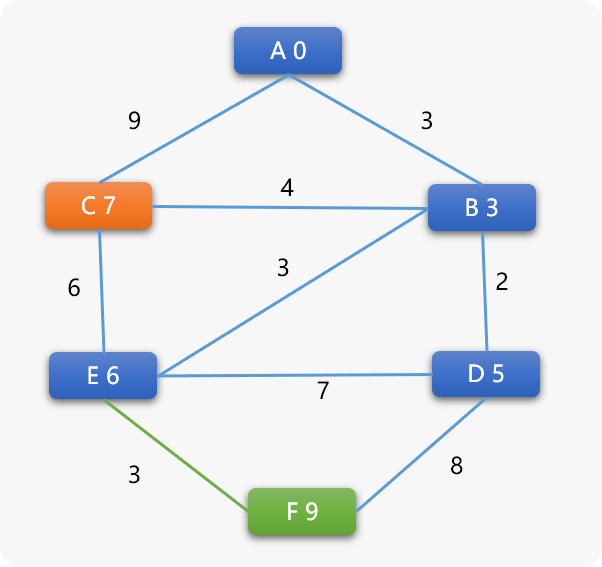
DJ05.png

  1. 再选择 C 为当前顶点
  • C 和相邻顶点不会再产生任何权重的变化，其前序顶点还是 B。 所以 A 到 C 之间的最短路径应该是 A->B->C 路径长度为 7。

DJ06.png

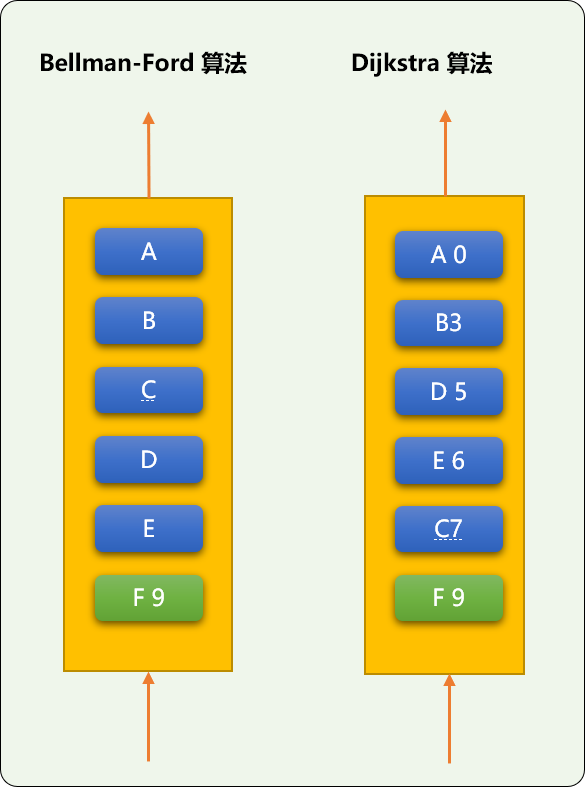
  • 最后选择 F 顶点，也不会再产生任何权重变化，F 的前序是 E，E的前序是B，B的前序是A，所 A 到 F 的最短路径应该是 A->B->E->F 权重值为 9。
  • 最后，以图示方式，比较 BF 算法和 DJ 算法中各顶点出队列的顺序。BF 采用就近原则出队列，然后不停计算相邻顶点的权重，直到权重不再变化为止，显然用的是蛮力，DJ 采用权重值小的优先出队列，显然用的是巧力。

dbdj.png

3.2 编码实现

分析完 DJ 算法流程，准备编码

和上面的 BF 算法相比较，顶点类一样，在图类中添加 DJ 算法。

DJ算法的本质还是广度优先搜索算法，有所区别的地方是使用优先队列，每次从队列中选择顶点时，选择顶点权重最小的。

所以需要在Graph类中添加优先队列对象，并为队列提供用于比较的函数对象。

//省略其它……
//为优先队列提供比较函数对象
struct comp {
	bool operator() (Vertex<T>* v1, Vertex<T>* v2) {
		//由小到大排列
		return v1->weight < v2->weight;
	}
};
template<typename T>
class Graph {
	private:
    	//省略其它……
    	//优先队列容器
		priority_queue<Vertex<T>* ,vector<Vertex<T>*>,comp<T> > priorityQueue;
    	//记录 Dj 算法已经更新顶点。 DJ 算法不需要对已经过求过权重的 2 个顶点重复计算
		vector< vector< Vertex<T>* > > isUpdate;
         //省略其它

DJ 算法函数

template<typename T>
class Graph {
    private:
    	//省略……
    public:
         //省略其它……
         /*
		*检查是否更新过
		*/
		bool isUpdated(Vertex<T>* v1,Vertex<T> * v2) {
			bool is=false;
			for(int i=0; i<this->isUpdate.size(); i++) {
				vector<Vertex<T>*> vec=this->isUpdate[i];
				if(v1==vec[0] && v2==vec[1] ||  v2==vec[0] && v1==vec[1] )is=true;
			}
			return is;
		}
		/*
		* Dijkstra（迪杰斯特拉）算法
		*/
		void djNearestPath(Vertex<T> * from_v) {
			// 记录边更新次数
			int update_count = 0;
			Vertex<T>* tmp_v;
			//设备起始点的权重为 0
			from_v->weight=0;
			// 起始点压入队列
			this->priorityQueue.push(from_v);
			//标记已经入队列
			from_v->visited = true;
			// 检查队列是否为空
			while ( !this->priorityQueue.empty() ) {
				// 从队列获取顶点
				tmp_v = this->priorityQueue.top();
				this->priorityQueue.pop();
				// 得到与其相邻所有顶点
				map< Vertex<T>*,int > nbr_vs = tmp_v->connectedTo;
				typename::std::map< Vertex<T>*,int >::iterator begin=nbr_vs.begin();
				typename::std::map< Vertex<T>*,int >::iterator end=nbr_vs.end();
				while(begin!=end) {
					Vertex<T>* v_=begin->first;
					// 顶点间的权重是否更新过
					if( this->isUpdated(tmp_v,v_))continue;
					// 更新权重
					tmp_v->calBfWeight(v_);
					//记录更新信息
					vector<Vertex<T>* > update= {tmp_v,v_ };
					// 把相邻顶点压入队列
					if( v_->visited==false ) {
						this->priorityQueue.push(v_);
						v_->visited=true;
					}
					begin++;
				}
			}
		}
    //省略其它……
};

测试代码：

int main(int argc, char** argv) {
	// 省略……
	Vertex<char>* fromV=   graph.findVert('A'); 
	cout<<"Dijkstra 算法:"<<endl; 
	graph.djNearestPath(fromV);
	cout<<"-------------------"<<endl;
	graph.findVertexes();
	graph.getAllPath('A');
	graph.showAllPath('A');
	return 0;
}

**输出结果：**和前面BF的结论一样。

DJ07.png

DJ 算法不适合用于边上权重为负数的图中，否则可能找不到路径。

3. 总结

在加权图中查找最短路径长度算法除了 BF、DJ 算法，还有 A* 算法 D* 算法。有兴趣的可以自行了解。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/152255.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

第五十讲：神州路由器IPv6隧道的配置

第五十讲：神州路由器IPv6隧道的配置

目前IPv6隧道技术有ISATAP隧道、6to4隧道、IPv6 over MPL隧道等。 任务一&#xff1a;配置ISATAP隧道 实验拓扑图如下所示 配置要求&#xff1a;两台路由器ROUTERA和ROUTERB通过IPv4网络连接&#xff0c;要求在两台路由器上分别配置ISATAP隧道&#xff0c;实现两端IPv6主机PC…
阅读更多...
回收租赁商城系统功能拆解05讲-供货商

回收租赁商城系统功能拆解05讲-供货商

回收租赁系统适用于物品回收、物品租赁、二手买卖交易等三大场景。 可以快速帮助企业搭建类似闲鱼回收/爱回收/爱租机/人人租等回收租赁商城。 回收租赁系统支持智能评估回收价格&#xff0c;后台调整最终回收价&#xff0c;用户同意回收后系统即刻放款&#xff0c;用户微信零…
阅读更多...
2022年学习和实习总结——收获颇多（未完待续...）

2022年学习和实习总结——收获颇多（未完待续...）

0 序言 时间已经进入了2023年&#xff0c;今年将是属于我们这一届秋招的一年。回顾2022年的学习和实习历程&#xff0c;我觉得今年的收获还是不少的&#xff0c;甚至可以说是整个高等教育生涯中&#xff0c;收获最多的一年。 1 学习情况总结 1.1 读书和学习总结 原来…
阅读更多...
【Linux】项目构建自动化工具——make和makefile

【Linux】项目构建自动化工具——make和makefile

make 和 makefile1.背景2. 利用make和makefile简单编译一个源文件3.使用方法解释4.执行原理5.项目清理1.背景 &#xff08;1&#xff09;一个工程中的源文件不计数&#xff0c;其按类型、功能、模块分别放在若干个目录中&#xff0c;makefile定义了一系列的规则来指定&#xff…
阅读更多...
智能驾驶视觉传感器测试：自动驾驶车辆如何进行传感器标定？

智能驾驶视觉传感器测试：自动驾驶车辆如何进行传感器标定？

为什么要进行标定&#xff1f;一辆自动驾驶车辆会安装多个传感器&#xff0c;需要通过传感器标定来确定相互之间的坐标关系&#xff0c;从而将多个传感器数据整合为“一个传感器”。因此&#xff0c;准确的传感器标定是实现智能车辆多传感器感知和定位系统的先决条件。传感器标…
阅读更多...
MXNet的Faster R-CNN(基于区域提议网络的实时目标检测)《6》

MXNet的Faster R-CNN(基于区域提议网络的实时目标检测)《6》

我们在看Faster R-CNN源码(MXNet版本)的时候&#xff0c;除了下面这些我们遇到的常见的参数解析 import argparse import ast parser argparse.ArgumentParser(descriptionDemonstrate a Faster R-CNN network,formatter_classargparse.ArgumentDefaultsHelpFormatter) parse…
阅读更多...
【操作系统系统/Golang】实验5：磁盘调度（FCFS,SSTF，SCAN与循环SCAN）

【操作系统系统/Golang】实验5：磁盘调度（FCFS,SSTF，SCAN与循环SCAN）

1 实验问题描述设计程序模拟先来先服务FCFS&#xff0c;最短寻道时间优先SSTF&#xff0c;SCAN和循环SCAN算法&#xff08;对应其他参考书的LOOK和C-LOOK&#xff09;的工作过程。假设有trackNum个磁道号所组成的磁道访问序列&#xff0c;给定开始磁道号initTrackNum和磁头移动…
阅读更多...
Java项目管理工具：Maven介绍

Java项目管理工具：Maven介绍

Maven 简介下载与环境配置Maven仓库仓库类型本地仓库配置简介 Maven ，一款跨平台的项目管理工具。它主要服务于基于 Java 平台的项目构建与依赖管理。即可以将项目的开发和管理过程抽象成一个项目对象模型（POM），开发人员只需要做一些简单的配置，Maven 便可自动完成项目构建…
阅读更多...
HRNet源码阅读笔记（4），庞大的PoseHighResolutionNet模块-stage1

HRNet源码阅读笔记（4），庞大的PoseHighResolutionNet模块-stage1

一、图和代码上一讲的图中&#xff0c;有stage1图例如下;关键是看pose_hrnet.py中PoseHighResolutionNet模块的forward函数相关部分如下&#xff1a;def forward(self, x):x self.conv1(x)x self.bn1(x)x self.relu(x)x self.conv2(x)x self.bn2(x)x self.relu(x)x self…
阅读更多...
一辈子干好一件事，你就了不起

一辈子干好一件事，你就了不起

人生的道路和轨迹&#xff0c;就像是射出去的箭。假如左拐右拐&#xff0c;不但不能射中靶心&#xff0c;达不到目标&#xff0c;还有可能拐弯回到原点&#xff0c;原地踏步。日复一日&#xff0c;年复一年&#xff0c;没有成长和收获&#xff0c;这很可怕。 短暂的2022年&…
阅读更多...
设计测试用例的万能公式 + 6大具体方法 = 面试就像聊天？

设计测试用例的万能公式 + 6大具体方法 = 面试就像聊天？

目录 一、设计测试用例的万能公式 二、设计测试用例的具体方法 2.1、等价类 2.2、边界值 2.3、判定表&#xff08;因果图的另一种形式&#xff09; 2.4、场景设计法 2.5、正交法&#xff08;用的少&#xff0c;基本不可见&#xff09; 2.4.1、使用allparis构建正交表 2.…
阅读更多...
算法之动态规划理论

算法之动态规划理论

目录 前言 一个模型三个特征理论讲解 1.最优子结构 2.无后效性 3.重复子问题 一个模型三个特征实例剖析 两种动态规划解题思路总结 1.状态转移表法 2.状态转移方程法 四种算法思想比较分析 总结&#xff1a; 参考资料 前言 本篇博文主要讲解动态规划的理论&am…
阅读更多...
行业分析| 交通综合执法对讲系统

行业分析| 交通综合执法对讲系统

随着社会的经济发展&#xff0c;人口的增加城市的不断壮大&#xff0c;城市交通情况越来越复杂&#xff0c;交警承担的执法任务越来越重&#xff0c;通信作为交警综合执法对讲调度的重要组成部分&#xff0c;也随之提出了更高的要求。综合执法对讲系统的出现使执法变得高效规范…
阅读更多...
【Redis】高级进阶

【Redis】高级进阶

&#x1f31f;个人博客&#xff1a;www.hellocode.top&#x1f31f; &#x1f31f;Java知识导航&#xff1a;Java-Navigate&#x1f31f; ⭐想获得更好的阅读体验请前往Java-Navigate &#x1f525;本文专栏&#xff1a;《流行框架》 &#x1f31e;如没有JavaWEB基础&#xff0…
阅读更多...
【ZooKeeper】第三章 集群搭建

【ZooKeeper】第三章 集群搭建

【ZooKeeper】第三章 集群搭建 文章目录【ZooKeeper】第三章 集群搭建一、ZooKeeper 集群介绍1.Leader 选举2.集群角色二、搭建 ZooKeeper 集群1.安装2.配置集群3.启动集群三、故障模拟一、ZooKeeper 集群介绍 1.Leader 选举 Serviceid&#xff1a;服务器 ID 比如有三台服务器…
阅读更多...
分享84个NET源码，总有一款适合您

分享84个NET源码，总有一款适合您

分享84个NET源码&#xff0c;总有一款适合您 链接&#xff1a;https://pan.baidu.com/s/1r7_yrTfQrg-5whL7AYJiLA?pwdeem6 提取码&#xff1a;eem6 import os from time import sleepimport requests from bs4 import BeautifulSoup from docx import Document from docx.sh…
阅读更多...
iOS ReplayKit 屏幕共享,屏幕直播实现

iOS ReplayKit 屏幕共享,屏幕直播实现

使用replayKit iOS12 之后相关 api 完成系统/app 内 屏幕采集直播视频数据, 采用 socket进行进程间Broadcast Unload Extension 向 宿主 app 传输数据, 后台保活持续采集屏幕数据, 摄像头采集, 数据编码解码 编译环境 Xcode14.2, iOS12 系统屏幕数据采集app 内屏幕共享使用so…
阅读更多...
FPGA与数字IC求职知识准备 - 数字电路知识总结

FPGA与数字IC求职知识准备 - 数字电路知识总结

前言 本文整理了数字电路课程中的相关基本的知识点和较为重要的知识点&#xff0c;用于求职的数电部分的知识准备&#xff0c;差缺补漏。 二进制数的算术运算 无符号二进制数的算术运算 加法&#xff1a;同十进制加法&#xff0c;逢二进一&#xff0c;无符号二进制数的加法…
阅读更多...
Redis源码篇(8)——集群模式

Redis源码篇(8)——集群模式

1、集群模式的启动和初始化 当开启了cluster-enabled&#xff0c;在初始化服务initServer方法中会调用clusterInit方法将redis带入cluster模式。 clusterInit void clusterInit(void) {int saveconf 0;//初始化clusterState结构 server.cluster zmalloc(sizeof(clusterSta…
阅读更多...
LaTeX代码宏包listings的使用

LaTeX代码宏包listings的使用

LaTeX代码宏包listings的使用 文章目录LaTeX代码宏包listings的使用1 需求2 verbatim环境简介3 listings设置代码高亮4 代码样式和颜色5 为listings添加题注6 listings支持的语言格式7 附录 listings样式的自定义参数1 需求 LaTeX\LaTeXLATE​X适合用来进行结构化文档的编辑。如…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023