🎉欢迎大家观看AUGENSTERN_dc的文章(o゜▽゜)o☆✨✨
🎉感谢各位读者在百忙之中抽出时间来垂阅我的文章,我会尽我所能向的大家分享我的知识和经验📖
🎉希望我们在一篇篇的文章中能够共同进步!!!
🌈个人主页:AUGENSTERN_dc
🔥个人专栏:C语言 | Java | 数据结构
⭐个人格言:
一重山有一重山的错落,我有我的平仄
一笔锋有一笔锋的着墨,我有我的舍得
目录
1. 定义:
2. 两种特殊的二叉树:
3. 二叉树的性质:
4. 二叉树的手动创建:
5. 二叉树的遍历:
5.1 前序遍历:
5.2 中序遍历:
5.3 后序遍历:
5.4 层序遍历:
6. 根据二叉树的遍历序列创建二叉树
6.1 根据二叉树的前序遍历和中序遍历创建二叉树:
6.2 根据二叉树的中序遍历和后序遍历创建二叉树:
7. 二叉树的基本操作:
8.二叉树相关整体源码分享:
在我之前的文章栈中讲到,栈可以将递归转化成循环,故二叉树的很多递归实现的操作,都可以依靠栈来转换成循环,并且写法并不困难,但在该篇文章中,我并没用用非递归的方法实现这些方法,如果有兴趣的朋友,可以自己尝试以下非递归的写法,也可以在评论区和我进行讨论,我会在第一时间进行回复,多多谅解!!!
1. 定义:
一颗二叉树是节点的有限集合,该集合:
< 1 > 或者为空;
< 2 > 或者是由一个根节点加上最多两棵分别称为左子树和右子树的二叉树组成。(左右子树可为空)
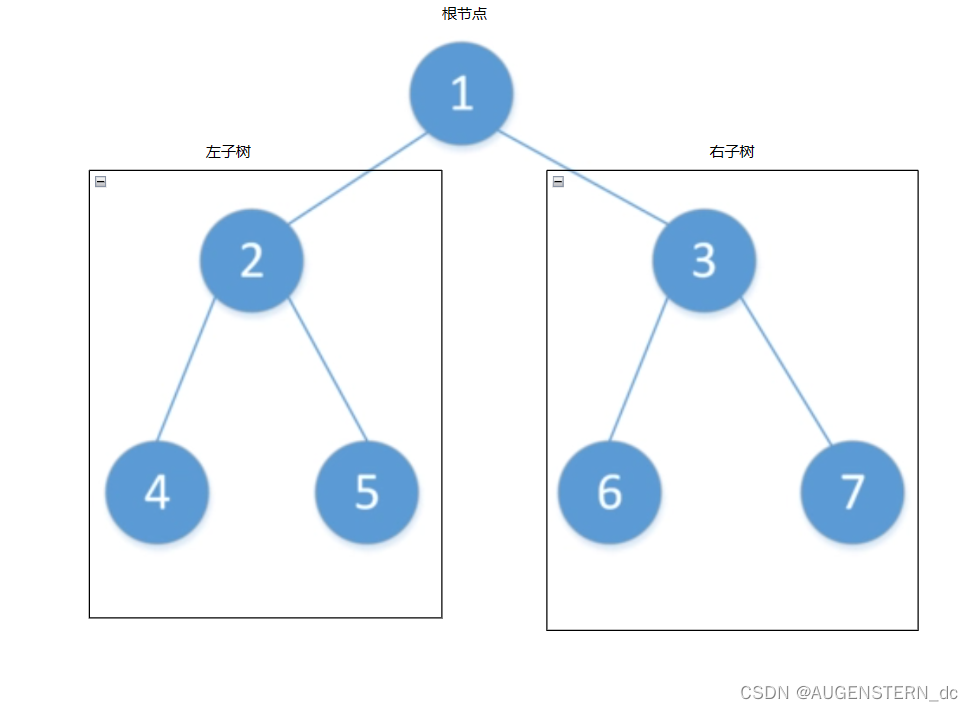
从上图可以看出:
< 1 > 二叉树不存在度大于2的节点;
< 2 > 二叉树的子树有左右子树之分,次序不能颠倒,所以二叉树是有序树;
对于任意的二叉树,都由以下几种情况复合而来的:

2. 两种特殊的二叉树:
< 1 > 一棵二叉树,如果每层的节点数都达到最大值,则这棵二叉树就是满二叉树。也就是说,如果一棵二叉树的层数为K,且节点总数是2的k次方 - 1,则它就是满二叉树。
< 2 > 完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n 个结点的二叉树,当且仅当其每一个节点都与深度为K的满二叉树中编号从0至n-1的节点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。


如上右图就是一颗满二叉树,左图是一棵完全二叉树;
3. 二叉树的性质:
< 1 > 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2的i - 1次方(i>0)个节点;
< 2 > 若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是2的k次方 - 1(k>=0);
< 3 > 对任何一棵二叉树, 如果其叶节点个数为 n0, 度为2的非叶节点个数为 n2,则有n0=n2+1;
< 4 > 具有n个节点的完全二叉树的深度k为log2(n + 1)上取整;
< 5 > 对于具有n个节点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i 的节点有:
- 若i>0,双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点;
- 若2i+1 < n,左孩子序号:2i+1,否则无左孩子;
- 若2i+2 < n,右孩子序号:2i+2,否则无右孩子;
// 孩子表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
Node parent; // 当前节点的根节点
}本文使用孩子表示法来构建二叉树
4. 二叉树的手动创建:
二叉树的基本操作包括遍历和创建,但是为了降低学习成本,我们先手动创建一棵二叉树,快速的进入二叉树的学习,等到时机成熟的时候,再写二叉树的常规创建的方法;
首先,我们需要构建一个二叉树类:
public class BinaryTree {
public static class TreeNode {
int val; //节点的值
TreeNode left; //节点的左子树
TreeNode right; //节点的右子树
public TreeNode (int val) { //构造方法
this.val = val;
}
}
private TreeNode root; //根节点
//用死板的方法创建一棵二叉树,真正的创建并非如此,这里只是为了前期的讲解和测试
public TreeNode createTree () {
TreeNode A = new TreeNode(1);
TreeNode B = new TreeNode(2);
TreeNode C = new TreeNode(3);
TreeNode D = new TreeNode(4);
TreeNode E = new TreeNode(5);
TreeNode F = new TreeNode(6);
TreeNode G = new TreeNode(7);
TreeNode H = new TreeNode(8);
A.left = B;
A.right = C;
B.left = D;
B.right = E;
C.left = F;
C.right = G;
D.left = H;
return A;
}
}在上文中我们讲到:
如果二叉树是一棵非空的树,那么他就由根节点和左子树,右子树组成,从概念中我们可以看出,二叉树的定义是递归式的,因此后续的操作都与递归有关;
5. 二叉树的遍历:
二叉树的遍历分为四种:
< 1 > 前序遍历
< 2 > 中序遍历
< 3 > 后序遍历
< 4 > 层序遍历
遍历:所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个节点均做一次且仅做一次访问。访问节点所做的操作依赖于具体的应用问题(例如打印节点内容,节点内容 + 1)
遍历是二叉树的最重要的操作之一,是二叉树上进行其他运算的基础!!!
5.1 前序遍历:
前序遍历又称为先序遍历:是先访问二叉树的根节点,再访问根的左子树,最后再访问根的右子树
如图所示:
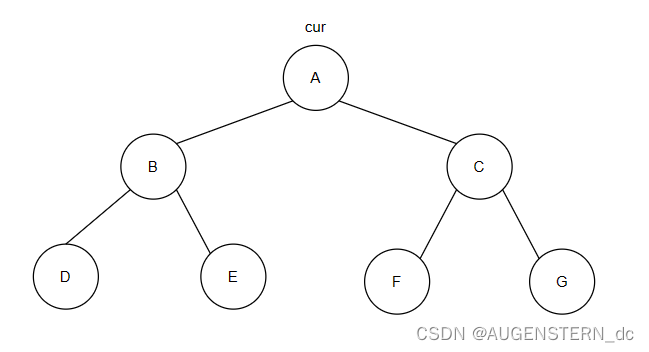
在这样一棵二叉树中,如果我们使用前序遍历,cur先访问根节点并打印,再访问根节点的左子树,也就是B节点,此时cur到达了B节点

此时的根节点也就变成了B节点,再打印我们的B节点,之后再访问根节点的左子树,也就是D节点,此时,cur来到了D节点;

再打印D节点,按照顺序,此时我们应该去访问D节点的左子树,但是,此时我们发现,D节点的左子树为空,那我们就访问D节点的右子树,但右子树也为空,那么说明,B节点的左子树的递归结束了,此时的cur返回到了B节点

因为B节点的左子树访问完毕,那么就应该开始访问B节点的右子树,也就是节点E;

同理,打印E节点,接着访问E节点的左子树和右子树,但是E节点的左子树和右子树都为空,那么说明E节点遍历完成了,cur返回B节点,B节点的左右子树也遍历完成了,那么就返回A节点,继续遍历A节点的右子树;
依次类推;那么最终的访问的节点次序也就是:
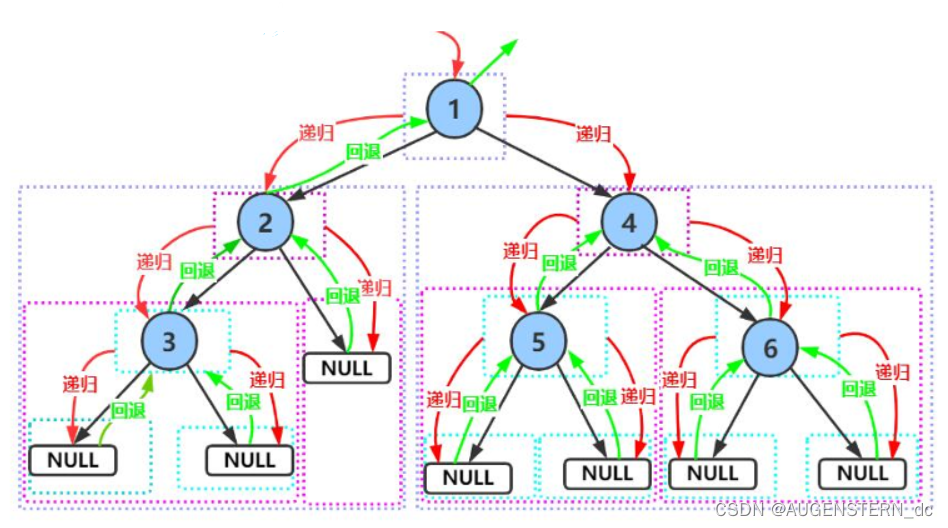
这就是前序遍历的全过程和顺序,其打印的结果也就是A B D E C F G;
代码的实现如下:
public void preOrder (TreeNode root) {
if (root == null) {
return;
}
System.out.print(root.val + " ");
preOrder(root.left);
preOrder(root.right);
}测试之后的结果是:
public class Main {
public static void main(String[] args) {
BinaryTree.TreeNode root;
BinaryTree tree = new BinaryTree();
root = tree.createTree();
tree.preOrder(root);
}
}
所打印的结果与我们模拟的结果一致:
5.2 中序遍历:
中序遍历的思路和前序遍历类似,但是中序遍历是先遍历左子树,在遍历根节点,最后再遍历右子树;
具体过程就不再描述了,可参考前序遍历;
依然是这样一棵树,中序遍历的结果应该为D B E A F C G;
public void inOrder (TreeNode root) {
if (root == null) {
return;
}
inOrder(root.left);
System.out.print(root.val + " ");
inOrder(root.right);
}测试的结果如图:
5.3 后序遍历:
后序遍历是先打印根节点的左子树,再打印根节点的右子树,最后再打印根节点
public void postOrder (TreeNode root) {
if (root == null) {
return;
}
postOrder(root.left);
postOrder(root.right);
System.out.print(root.val + " ");
}打印的结果如下图:

5.4 层序遍历:
层序遍历就和之前的遍历思路不一样了;
继续使用之前的二叉树的图:

层序遍历: 设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
如上图所示,层序遍历的结果应该是 A B C D E F G
如果要使用层序遍历遍历二叉树的节点,那么就需要使用到之前我们学习的数据结构,也就是队列:
以上图为例:
我们要想按每一层的从左到右的顺序来打印二叉树,我们就需要将二叉树的每一层的节点从左到右存在某一种结构中,再这种情况下,我们使用栈来存放二叉树的节点;
首先我们先创建一个队列,我们先将A节点存入队列中
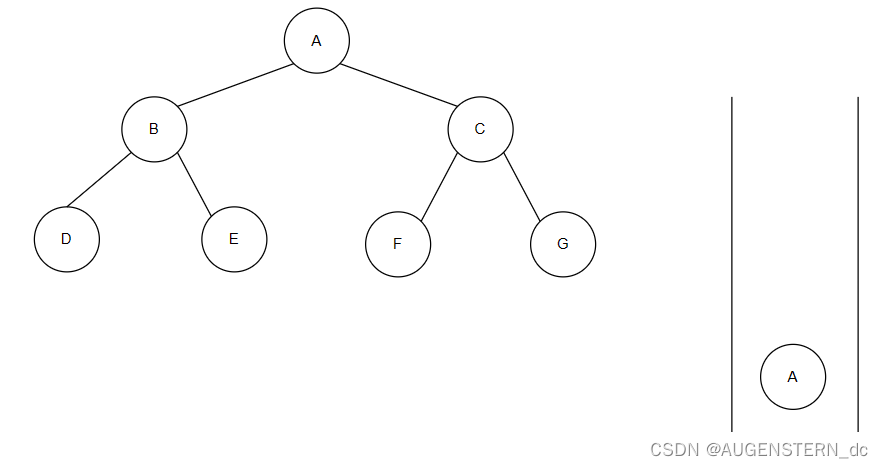
我们将队列中的队头元素,也就是A节点弹出来并进行打印,再判断A节点有没有左右子树,如果有,则先将左子树进行入队操作,再对右子树进行入队操作,若只有一个左子树或者右子树,只对左子树或者右子树进行入队操作;
在该过程中,我们先将A弹出,对A节点进行判断并打印A节点的值,再将C节点入队,最后将B节点入队;
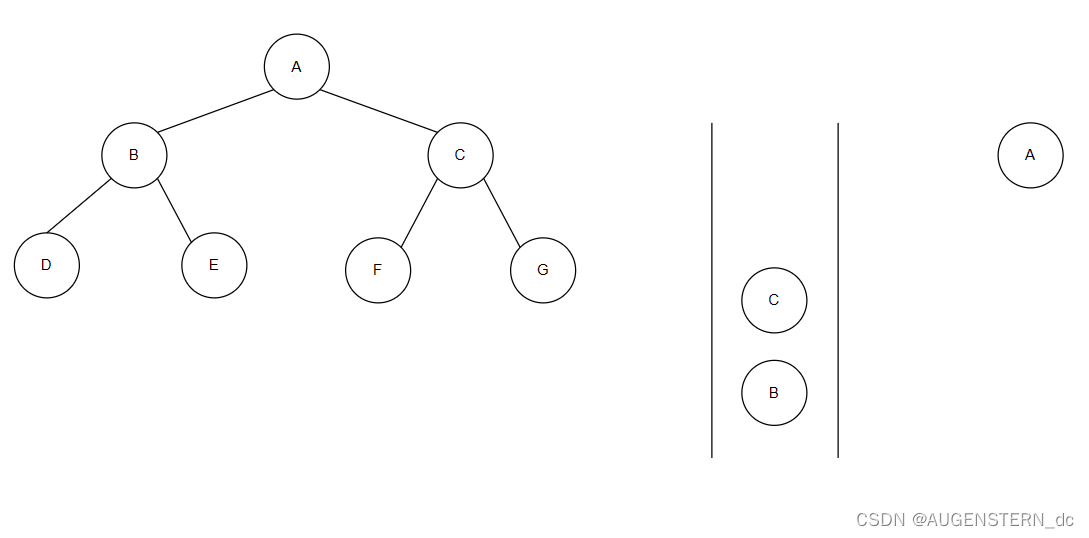
再次进行上述操作,将队头元素进行出队操作,也就是将B节点出队并进行打印,判断B节点是否有左右子树,对其左右子树进行入队操作;
在该过程中,将B节点进行出队操作并打印B节点的值,对B节点进行判断,再将D节点进行入队操作,最后对E节点进行入队操作;
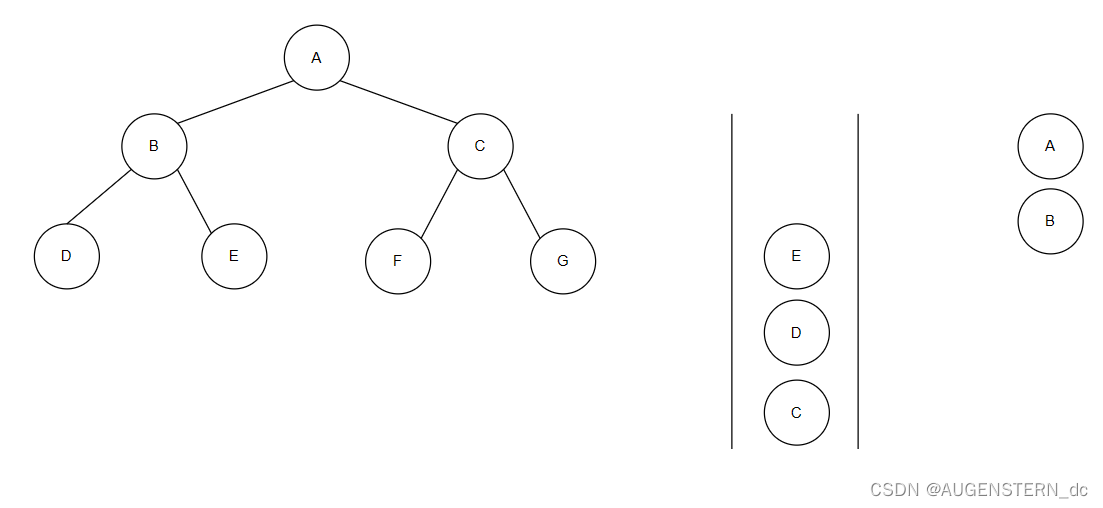
再将队头元素,也就是C节点进行出队操作,并打印C节点的值,再将F节点和G节点进行入队操作;

我们会发现,此时,我们只需将队列中的元素依次出队并打印,就可以得到层序遍历的打印结果,这就是层序遍历的代码实现思路:
代码如下:
public void levelOrder (TreeNode root) {
if (root == null) {
return;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
System.out.print(cur.val + " ");
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
}测试的结果如下:
6. 根据二叉树的遍历序列创建二叉树
6.1 根据二叉树的前序遍历和中序遍历创建二叉树:
·我们知道,前序遍历的遍历顺序是根节点,左子树,右子树,那么,前序遍历的第一个元素,也就是整棵树的根节点;
而中序遍历的顺序是左子树,根节点,右子树,那么,只要我们在中序遍历中找到二叉树的根节点,他的左边的元素都是他的左树,右边的元素都是他的右树;
如图:
依然用之前的二叉树的图

该树的前序遍历的结果为: A B D E C F G;
中序遍历的结果为:D B E A F C G;
在前序遍历中找到树的根节点,也就是A,在中序遍历中找到A节点的位置,则A节点的左边都是A节点的左子树,A节点的右边都是A节点的右子树,我们继续在前序遍历中找下一个根节点B,在中序遍历中找到B节点的位置,则B节点的左边是B节点的左子树,B节点的右边(到A节点为止)都是B节点的右子树,依次类推,我们就可以根据前序遍历和中序遍历序列来构建一个完整的二叉树;
代码如下:
public TreeNode preAndInBuildBinaryTree (char[] preOrder, char[] inOrder) {
return preAndInBuildBinaryTree(preOrder, 0, preOrder.length - 1, inOrder, 0, inOrder.length - 1);
}
private TreeNode preAndInBuildBinaryTree (char[] preOrder, int start1, int end1, char[] inOrder, int start2, int end2) {
if (start1 > end1 || start2 > end2) {
return null;
}
TreeNode root = new TreeNode(preOrder[start1]);
for (int i = start2; i <= end2; i++) {
if (inOrder[i] == preOrder[start1]) {
root.left = preAndInBuildBinaryTree(preOrder, start1 + 1, start1 + i - start2, inOrder, start2, i - 1);
root.right = preAndInBuildBinaryTree(preOrder, i - start2 + start1 + 1, end1, inOrder, i + 1, end2);
break;
}
}
return root;
}运行结果如下:
public class Main {
public static void main(String[] args) {
BinaryTree.TreeNode root;
BinaryTree tree = new BinaryTree();
char[] pre = {'A', 'B', 'D', 'E', 'C', 'F', 'G'};
char[] in = {'D', 'B', 'E', 'A', 'F', 'C', 'G'};
char[] post = {'D', 'E', 'B', 'F', 'G', 'C', 'A'};
root = tree.preAndInBuildBinaryTree(pre , in);
System.out.println( );
}
}
6.2 根据二叉树的中序遍历和后序遍历创建二叉树:
方法类似于前序遍历和中序遍历构建二叉树,具体的思路就不再写了;
代码如下:
public TreeNode inAndPostBuildBinaryTree (char[] postOrder, char[] inOrder) {
return inAndPostBuildBinaryTree(postOrder, 0, postOrder.length - 1, inOrder, 0, inOrder.length - 1);
}
// char[] in = {'D', 'B', 'E', 'A', 'F', 'C', 'G'};
// char[] post = {'D', 'E', 'B', 'F', 'G', 'C', 'A'};
private TreeNode inAndPostBuildBinaryTree (char[] postOrder, int start1, int end1, char[] inOrder, int start2, int end2) {
if (start1 > end1 || start2 > end2) {
return null;
}
TreeNode root = new TreeNode(postOrder[end1]);
for (int i = start2; i <= end2; i++) {
if (inOrder[i] == postOrder[end1]) {
root.left = inAndPostBuildBinaryTree(postOrder, start1, start1 + i - start2 - 1, inOrder, start2, i - 1);
root.right = inAndPostBuildBinaryTree(postOrder, i - start2 + start1, end1 - 1, inOrder, i + 1, end2);
break;
}
}
return root;
}运行结果如下:
public class Main {
public static void main(String[] args) {
BinaryTree.TreeNode root;
BinaryTree tree = new BinaryTree();
char[] pre = {'A', 'B', 'D', 'E', 'C', 'F', 'G'};
char[] in = {'D', 'B', 'E', 'A', 'F', 'C', 'G'};
char[] post = {'D', 'E', 'B', 'F', 'G', 'C', 'A'};
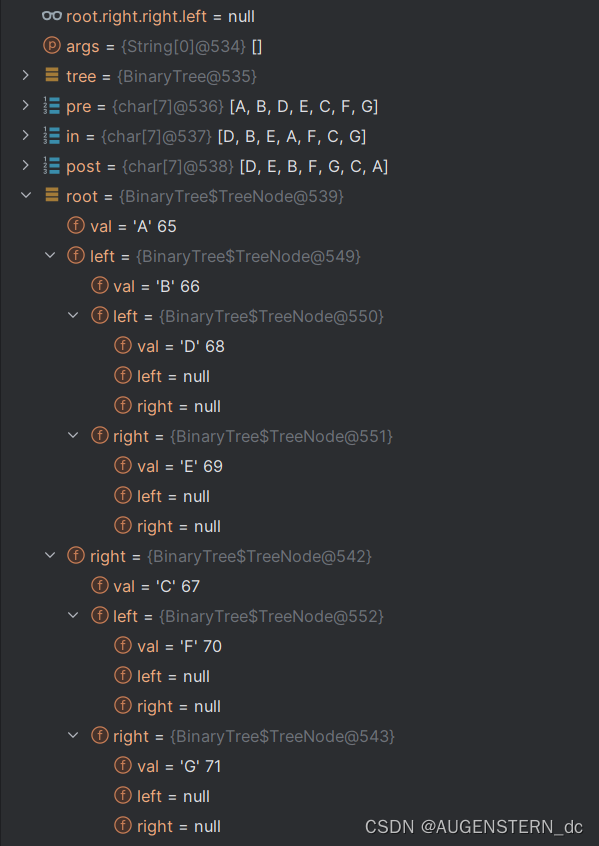
root = tree.inAndPostBuildBinaryTree(post , in);
}
}
7. 二叉树的基本操作:
接下来的内容相较于二叉树的创建,显得就简单很多了:
< 1 > 获取树中节点的个数:
一般来说,解决二叉树问题的核心关键就是递归,二叉树的总节点个数 = 左子树节点个数 + 右子树节点个数 + 1;
所以我们的代码可以写成:
public int getNodeCount (TreeNode root) {
if (root == null) { //若节点为空,返回0
return 0;
}
int leftCount = getNodeCount(root.left); //记录左子树的节点个数
int rightCount = getNodeCount(root.right); //记录右子树的节点个数
return leftCount + rightCount + 1; //返回左子树节点个数 + 右子树的节点个数 + 1
}运行结果如下 :
public class Main {
public static void main(String[] args) {
BinaryTree.TreeNode root;
BinaryTree tree = new BinaryTree();
char[] pre = {'A', 'B', 'D', 'E', 'C', 'F', 'G'};
char[] in = {'D', 'B', 'E', 'A', 'F', 'C', 'G'};
char[] post = {'D', 'E', 'B', 'F', 'G', 'C', 'A'};
root = tree.inAndPostBuildBinaryTree(post , in);
System.out.println(tree.getNodeCount(root));
}
} 
< 2 > 获取树中叶子节点的个数:
获取叶子节点的个数和获取树的节点的个数的思路大致类似,树的总节点的个数是遇到节点就++,而叶子节点的个数是遇到左右子树为空的节点就++;
代码如下:
public int getLeavesNodeCount (TreeNode root) {
if (root.left == null && root.right == null) { //若左右子树都为空,则该节点为叶子节点,返回1
return 1;
}
int leftCount = getLeavesNodeCount(root.left); //左子树的叶子节点个数
int rightCount = getLeavesNodeCount(root.right); //右子树的叶子节点个数
return leftCount + rightCount; //返沪左子树叶子节点个数 + 右子树叶子节点个数
}运行结果如下:
public class Main {
public static void main(String[] args) {
BinaryTree.TreeNode root;
BinaryTree tree = new BinaryTree();
char[] pre = {'A', 'B', 'D', 'E', 'C', 'F', 'G'};
char[] in = {'D', 'B', 'E', 'A', 'F', 'C', 'G'};
char[] post = {'D', 'E', 'B', 'F', 'G', 'C', 'A'};
root = tree.inAndPostBuildBinaryTree(post , in);
System.out.println(tree.getLeavesNodeCount(root));
}
}
< 3 > 获取树第k层节点的个数:
要想获得第k层的节点个数,我们只需要使用一个计数器,去控制递归的深度为k即可
代码如下:
public int getKNodeCount (TreeNode root, int k) {
return getKNodeCount(root, k, 1);
}
private int getKNodeCount (TreeNode root, int k, int count) {
if (root == null) {
return 0;
}
if (k == count) {
return 1;
}
return getKNodeCount(root.left, k, count + 1) + getKNodeCount(root.right, k, count + 1);
}测试结果如下:
public class Main {
public static void main(String[] args) {
BinaryTree.TreeNode root;
BinaryTree tree = new BinaryTree();
char[] pre = {'A', 'B', 'D', 'E', 'C', 'F', 'G'};
char[] in = {'D', 'B', 'E', 'A', 'F', 'C', 'G'};
char[] post = {'D', 'E', 'B', 'F', 'G', 'C', 'A'};
root = tree.inAndPostBuildBinaryTree(post , in);
System.out.println(tree.getKNodeCount(root, 3));
}
}
< 4 > 获取二叉树的高度:
二叉树的高度是左右子树中最高的一颗树决定的,所以二叉树的高度就为左右子树的高度的最大值:
代码如下:
public int getHeight (TreeNode root) {
if (root == null) {
return 0;
}
int left = getHeight(root.left) + 1; //左子树高度
int right = getHeight(root.right) + 1; //右子树高度
return Math.max(left, right); //返回左右子树的高度的最大值
}测试结果如下:
public class Main {
public static void main(String[] args) {
BinaryTree.TreeNode root;
BinaryTree tree = new BinaryTree();
char[] pre = {'A', 'B', 'D', 'E', 'C', 'F', 'G'};
char[] in = {'D', 'B', 'E', 'A', 'F', 'C', 'G'};
char[] post = {'D', 'E', 'B', 'F', 'G', 'C', 'A'};
root = tree.inAndPostBuildBinaryTree(post , in);
System.out.println(tree.getHeight(root));
}
}
< 5 > 检测值为value的节点是否存在:
想要检测value的值是否存在,只需左子树或者右子树中或者根节点的值为value即可:
代码如下:
public boolean exiteValue (TreeNode root, char value) {
if (root == null) {
return false; // 如果节点为空了,则不存在,返回false
}
if (root.val == value) {
return true; //若节点值和value相等,返回true
}
return exiteValue(root.left, value) || exiteValue(root.right, value); //返回左子树是否有该值 或者 右子树是否有该值
}测试结果如下:
public class Main {
public static void main(String[] args) {
BinaryTree.TreeNode root;
BinaryTree tree = new BinaryTree();
char[] pre = {'A', 'B', 'D', 'E', 'C', 'F', 'G'};
char[] in = {'D', 'B', 'E', 'A', 'F', 'C', 'G'};
char[] post = {'D', 'E', 'B', 'F', 'G', 'C', 'A'};
root = tree.inAndPostBuildBinaryTree(post , in);
System.out.println(tree.exiteValue(root, 'G'));
}
}
< 6 > 判断一棵树是不是完全二叉树:
想要判断一棵树是不是完全二叉树,我们可以创建一个队列,将跟节点的进行入队操作,将根节点弹出后,判断根节点的左子树是否为空,若不为空,则将其左子树入队,若为空,则将null入队,右子树同理,若队列弹出的元素为空,则跳出循环,进行下一个循环判断,若队列中的元素都为空,则该树为完全二叉树,若该队列中的元素不都为空,则该树不是完全二叉树;
代码如下:
public boolean isCompleteBinaryTree (TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
if (cur == null) {
break;
}
if (cur.left != null) {
queue.offer(cur.left);
} else {
queue.offer(null);
}
if (cur.right != null) {
queue.offer(cur.right);
} else {
queue.offer(null);
}
}
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
if (cur != null) {
return false;
}
}
return true;
}测试结果如下:
public static void main(String[] args) {
BinaryTree.TreeNode root;
BinaryTree tree = new BinaryTree();
char[] pre = {'A', 'B', 'D', 'E', 'C', 'F', 'G'};
char[] in = {'D', 'B', 'E', 'A', 'F', 'C', 'G'};
char[] post = {'D', 'E', 'B', 'F', 'G', 'C', 'A'};
root = tree.inAndPostBuildBinaryTree(post , in);
System.out.println(tree.isCompleteBinaryTree(root));
}
8.二叉树相关整体源码分享:
import java.util.LinkedList;
import java.util.Queue;
public class BinaryTree {
public static class TreeNode {
char val; //节点的值
TreeNode left; //节点的左子树
TreeNode right; //节点的右子树
public TreeNode (char val) { //构造方法
this.val = val;
}
}
//public TreeNode root; //根节点
//用死板的方法创建一棵二叉树,真正的创建并非如此,这里只是为了前期的讲解和测试
public TreeNode createTree () {
TreeNode A = new TreeNode('A');
TreeNode B = new TreeNode('B');
TreeNode C = new TreeNode('C');
TreeNode D = new TreeNode('D');
TreeNode E = new TreeNode('E');
TreeNode F = new TreeNode('F');
TreeNode G = new TreeNode('G');
A.left = B;
A.right = C;
B.left = D;
B.right = E;
C.left = F;
C.right = G;
return A;
}
void preOrder (TreeNode root) {
if (root == null) {
return;
}
System.out.print(root.val + " ");
preOrder(root.left);
preOrder(root.right);
}
void inOrder (TreeNode root) {
if (root == null) {
return;
}
inOrder(root.left);
System.out.print(root.val + " ");
inOrder(root.right);
}
public void postOrder (TreeNode root) {
if (root == null) {
return;
}
postOrder(root.left);
postOrder(root.right);
System.out.print(root.val + " ");
}
public void levelOrder (TreeNode root) {
if (root == null) {
return;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
System.out.print(cur.val + " ");
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
}
public TreeNode preAndInBuildBinaryTree (char[] preOrder, char[] inOrder) {
return preAndInBuildBinaryTree(preOrder, 0, preOrder.length - 1, inOrder, 0, inOrder.length - 1);
}
private TreeNode preAndInBuildBinaryTree (char[] preOrder, int start1, int end1, char[] inOrder, int start2, int end2) {
if (start1 > end1 || start2 > end2) {
return null;
}
TreeNode root = new TreeNode(preOrder[start1]);
for (int i = start2; i <= end2; i++) {
if (inOrder[i] == preOrder[start1]) {
root.left = preAndInBuildBinaryTree(preOrder, start1 + 1, start1 + i - start2, inOrder, start2, i - 1);
root.right = preAndInBuildBinaryTree(preOrder, i - start2 + start1 + 1, end1, inOrder, i + 1, end2);
break;
}
}
return root;
}
public TreeNode inAndPostBuildBinaryTree (char[] postOrder, char[] inOrder) {
return inAndPostBuildBinaryTree(postOrder, 0, postOrder.length - 1, inOrder, 0, inOrder.length - 1);
}
// char[] in = {'D', 'B', 'E', 'A', 'F', 'C', 'G'};
// char[] post = {'D', 'E', 'B', 'F', 'G', 'C', 'A'};
private TreeNode inAndPostBuildBinaryTree (char[] postOrder, int start1, int end1, char[] inOrder, int start2, int end2) {
if (start1 > end1 || start2 > end2) {
return null;
}
TreeNode root = new TreeNode(postOrder[end1]);
for (int i = start2; i <= end2; i++) {
if (inOrder[i] == postOrder[end1]) {
root.left = inAndPostBuildBinaryTree(postOrder, start1, start1 + i - start2 - 1, inOrder, start2, i - 1);
root.right = inAndPostBuildBinaryTree(postOrder, i - start2 + start1, end1 - 1, inOrder, i + 1, end2);
break;
}
}
return root;
}
public int getNodeCount (TreeNode root) {
if (root == null) { //若节点为空,返回0
return 0;
}
int leftCount = getNodeCount(root.left); //记录左子树的节点个数
int rightCount = getNodeCount(root.right); //记录右子树的节点个数
return leftCount + rightCount + 1; //返回左子树节点个数 + 右子树的节点个数 + 1
}
public int getLeavesNodeCount (TreeNode root) {
if (root.left == null && root.right == null) { //若左右子树都为空,则该节点为叶子节点,返回1
return 1;
}
int leftCount = getLeavesNodeCount(root.left); //左子树的叶子节点个数
int rightCount = getLeavesNodeCount(root.right); //右子树的叶子节点个数
return leftCount + rightCount; //返沪左子树叶子节点个数 + 右子树叶子节点个数
}
public int getKNodeCount (TreeNode root, int k) {
return getKNodeCount(root, k, 1);
}
private int getKNodeCount (TreeNode root, int k, int count) {
if (root == null) {
return 0;
}
if (k == count) {
return 1;
}
return getKNodeCount(root.left, k, count + 1) + getKNodeCount(root.right, k, count + 1);
}
public int getHeight (TreeNode root) {
if (root == null) {
return 0;
}
int left = getHeight(root.left) + 1; //左子树高度
int right = getHeight(root.right) + 1; //右子树高度
return Math.max(left, right); //返回左右子树的高度的最大值
}
public boolean exiteValue (TreeNode root, char value) {
if (root == null) {
return false; // 如果节点为空了,则不存在,返回false
}
if (root.val == value) {
return true; //若节点值和value相等,返回true
}
return exiteValue(root.left, value) || exiteValue(root.right, value); //返回左子树是否有该值 或者 右子树是否有该值
}
public boolean isCompleteBinaryTree (TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
if (cur == null) {
break;
}
if (cur.left != null) {
queue.offer(cur.left);
} else {
queue.offer(null);
}
if (cur.right != null) {
queue.offer(cur.right);
} else {
queue.offer(null);
}
}
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
if (cur != null) {
return false;
}
}
return true;
}
}以上就是二叉树的全部内容,感谢大家观看,谢谢!!!!!
制作不易,三连支持谢谢!!!
以上的模拟实现代码未必是最优解,仅代表本人的思路,望多多理解,谢谢!!
最后送给大家一句话,同时也是对我自己的勉励:
不是看到了希望才去坚持,而是坚持了才能看到希望!!!!!