[5]. 最长回文子串

news2025/1/19 23:27:51

[5]. 最长回文子串

题目
算法设计：双指针
算法设计：Manacher 算法

题目

传送门：https://leetcode.cn/problems/longest-palindromic-substring/

算法设计：双指针

检查回文串的通用解决方案是，双指针。

寻找回文串的思想是：从中间开始向俩边扩散来判断回文串。

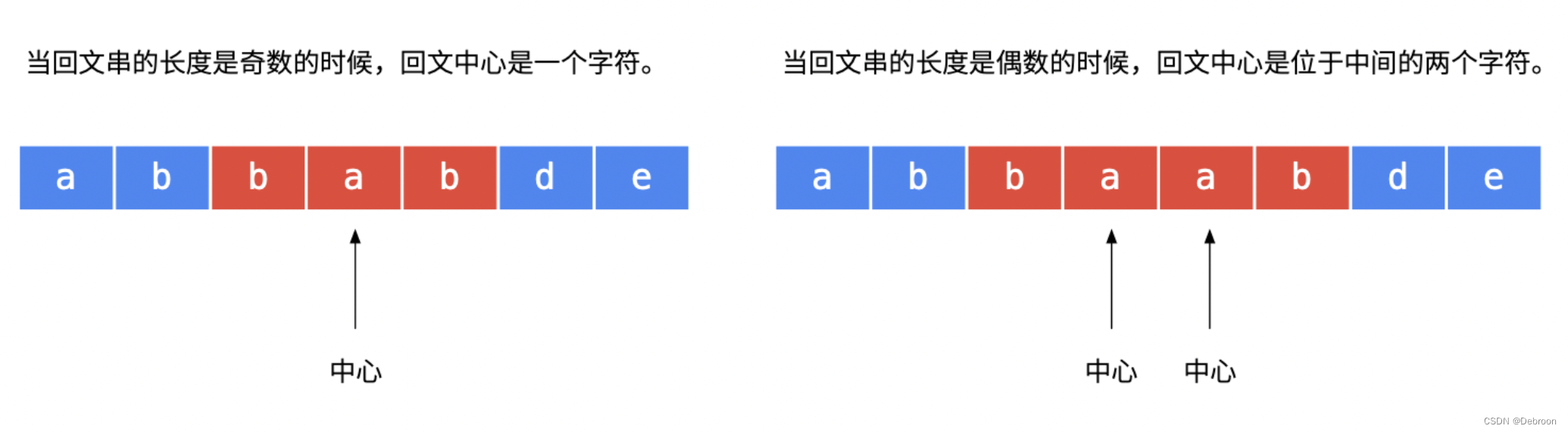
回文串在长度为奇数和偶数的时候，中心不一样：

奇数回文串的「中心」是一个具体的字符，如回文串 aba 的中心是字符 b；
偶数回文串的「中心」是位于中间的两个字符的「空隙」，如回文串 abba 的中心是两个 b，也可以看成两个 b 中间的空隙。

for(int i=0; i<len(s); i++)
	奇数：找到以 s[i] 为中心的回文串
	偶数：找到以 s[i] 和 s[i+1] 为中心的回文串
	根据找到的回文串，更新最长子串

代码实现：

class Solution {
	string res;
public:
    string mid(string& s, int l, int r) {               // 中心扩散，俩指针可同时处理回文长度为奇数、偶数情况
	    while( s[l] == s[r] && l>=0 && r<s.size() )     // 如果对应相等，是回文 && 判断边界
		    l --, r ++;                                 // 从中心扩散，去探下一个位置
	    return s.substr( l + 1, r - l - 1 );            // 最长回文串，从指定位置开始，复制指定的长度
    }

    string max3(string res, string s1, string s2) {     // 寻找最长串
        res = res.size() > s1.size() ? res : s1;
        res = res.size() > s2.size() ? res : s2;
        return res;
    }

    string longestPalindrome(string s) {
		for(int i=0; i<s.size(); i++) {
			string s1 = mid(s, i, i);                  // 寻找奇数回文子串
			string s2 = mid(s, i, i+1);                // 寻找偶数回文子串
			res = max3(res, s1, s2);                   // 最长回文子串
		}
		return res;
    }
};

代码思路如上，不过执行出错，不知道是哪里的问题。

class Solution {
public:
    string longestPalindrome(string s) {
        int len = s.size(), maxLen = 1, begin = 0;
        // 从第一个字符出发
        int centL = 0, centR = 0;
        while (centR < len) {
            int l = centL;       // 左中心
            int r = centR;       // 右中心
            while (l >= 0 && r < len && s[l] == s[r]) // 数组不会越界 && 相等 
                l--, r++;        // 从中心扩散
            if (maxLen < (r - l - 1)) {
                maxLen = r - l - 1;
                begin = l + 1;
            }
            // 当前 centL 与 centR 指向同一个字符串时，centR 向右移动一格
            // 当前 centR 在 centL 的右侧时(两个指针最多相差一个)，centL 向右移动一格
            centR > centL ? ++centL : ++centR;
        }
        return s.substr(begin, maxLen);
    }
};