一、写在前面
许久没有写图形化界面的程序了,最近学习了一些经典的盲目搜索算法与智能搜索算法,正好拿来还原三阶魔方!试试手!
提前声明
我不是专业搞人工智能的,理论或者实现过程有些许错误也很正常,评论区指出即可
先说一下开发环境吧!源码及打包程序的下载链接放在文末!
1.1 开发环境
编程语言:Python 3.12
图形界面库:tkintertools 2.6.21.1(底层为 tkinter)
第三方依赖库:tkintertools 2.6.21.1(就这么一个)
二、程序概览
2.1 代码情况
代码量:1000 行左右
代码大小:34KB
2.2 图片展示
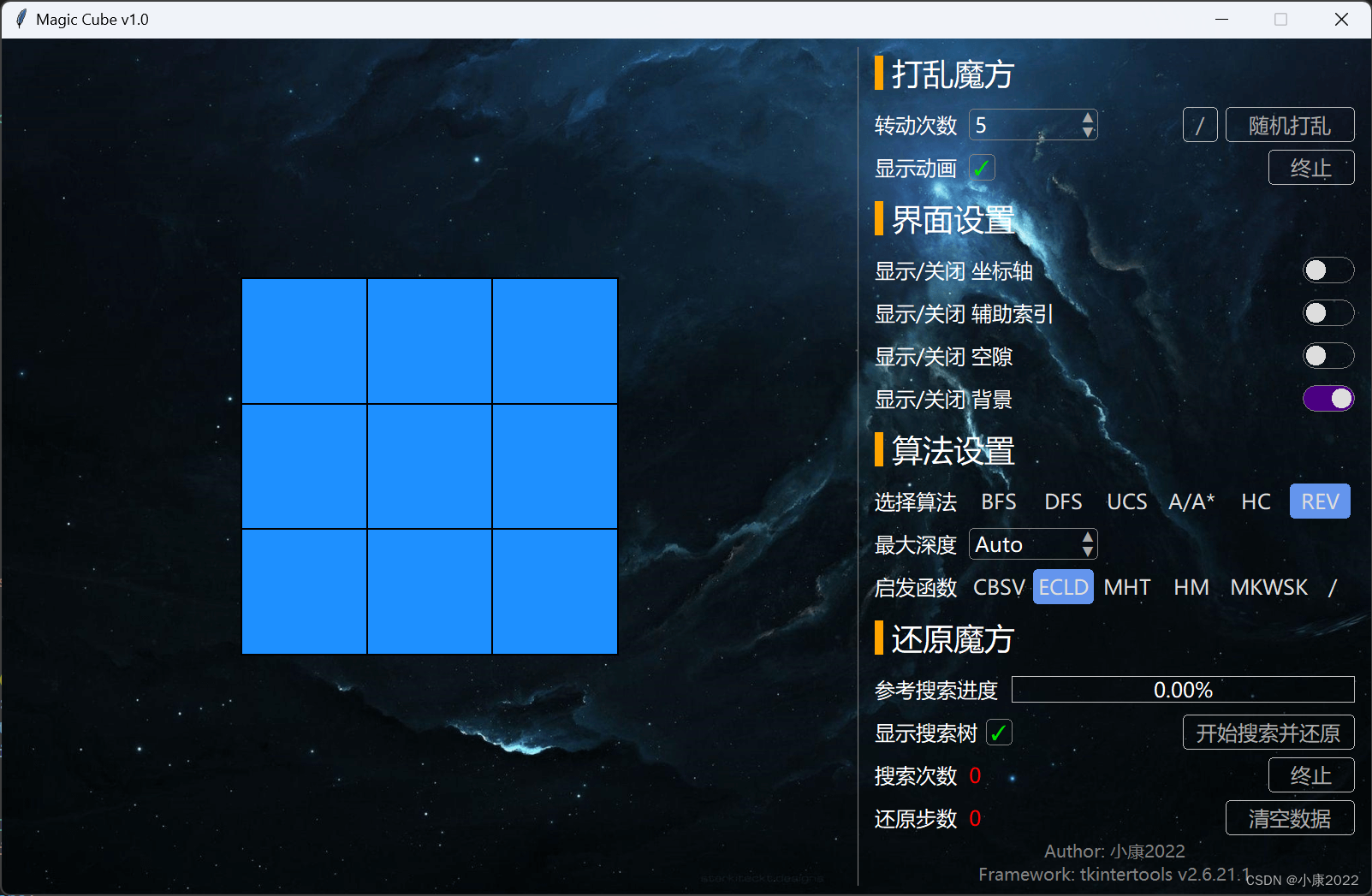
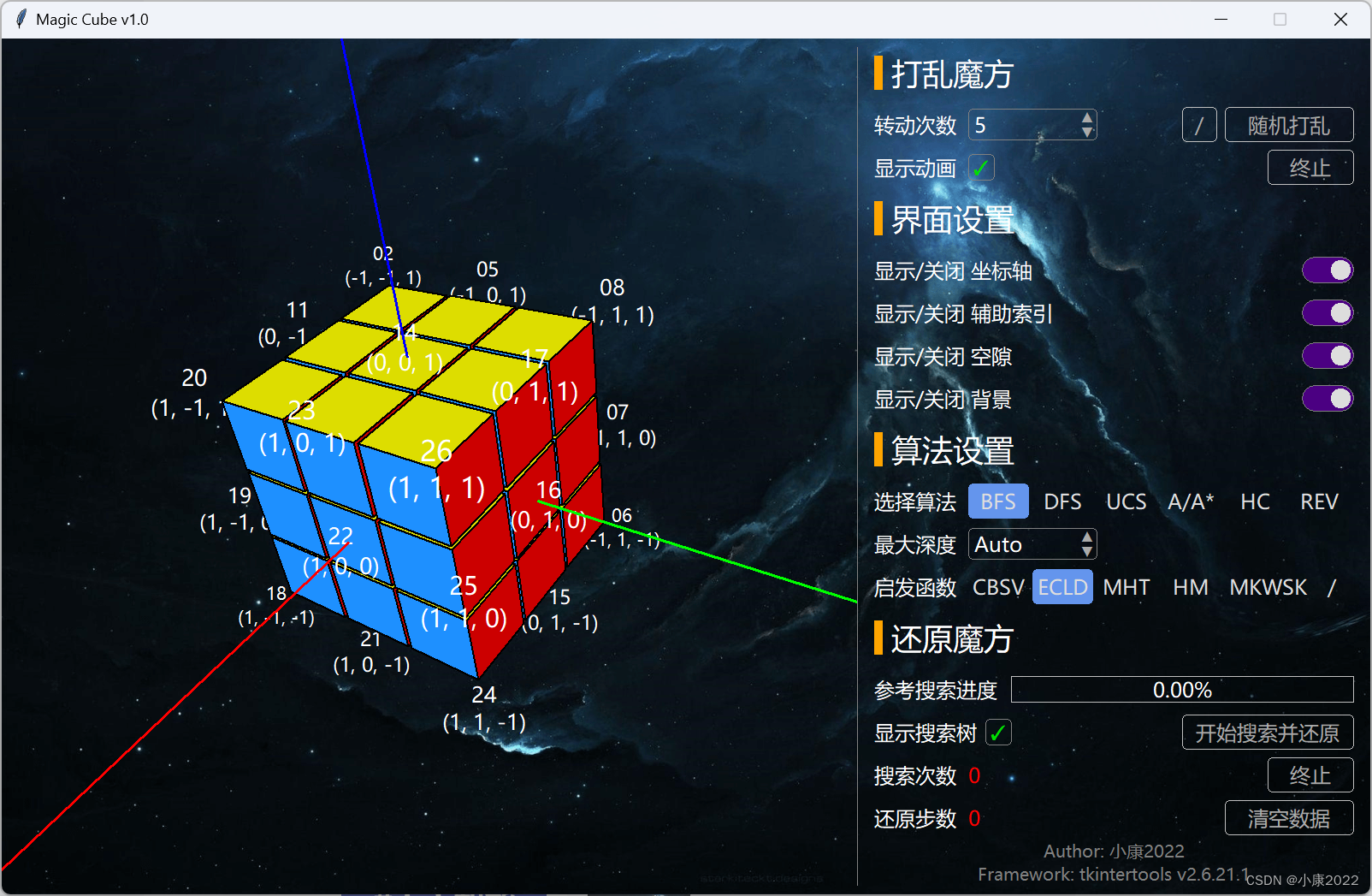
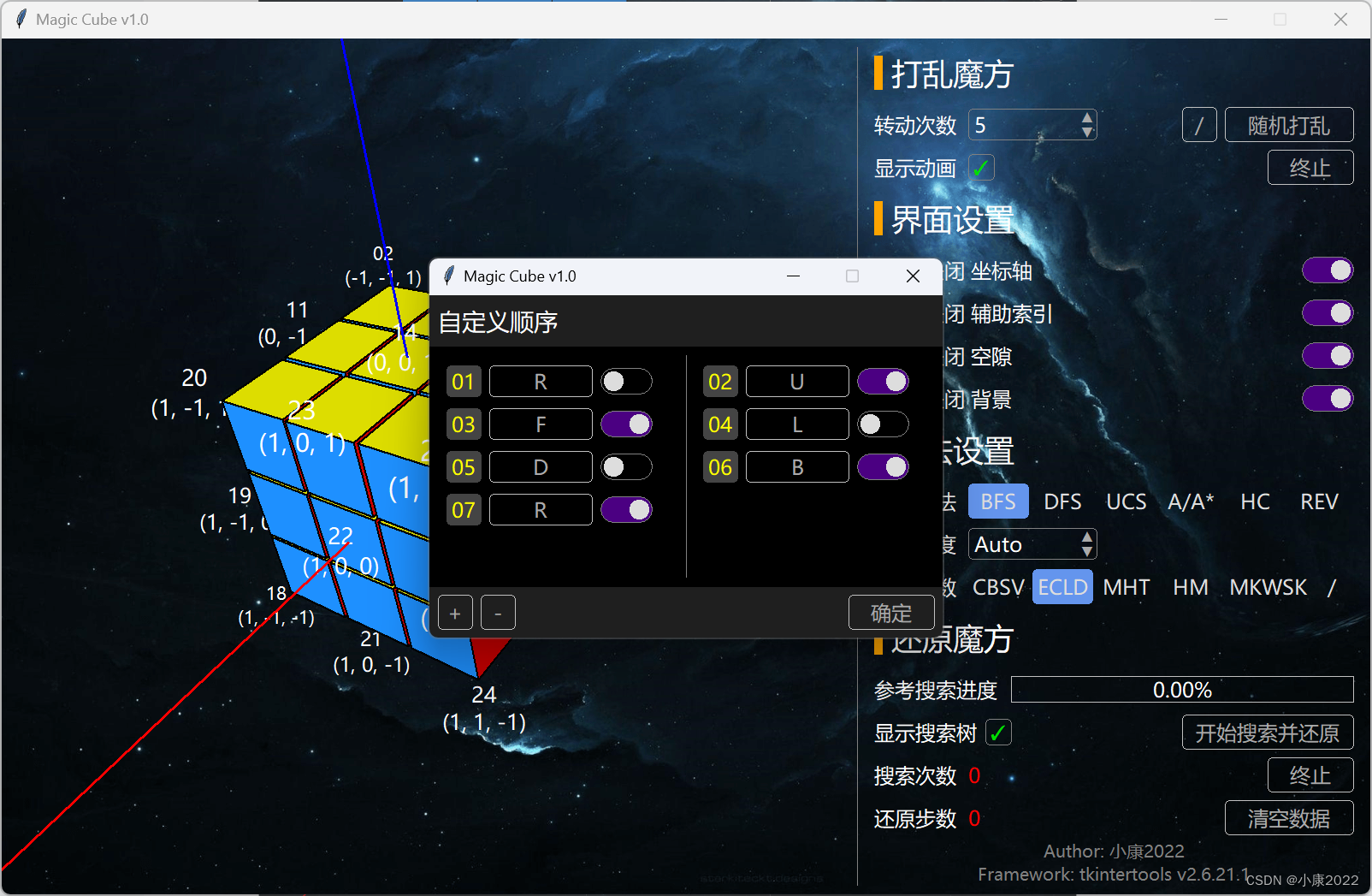
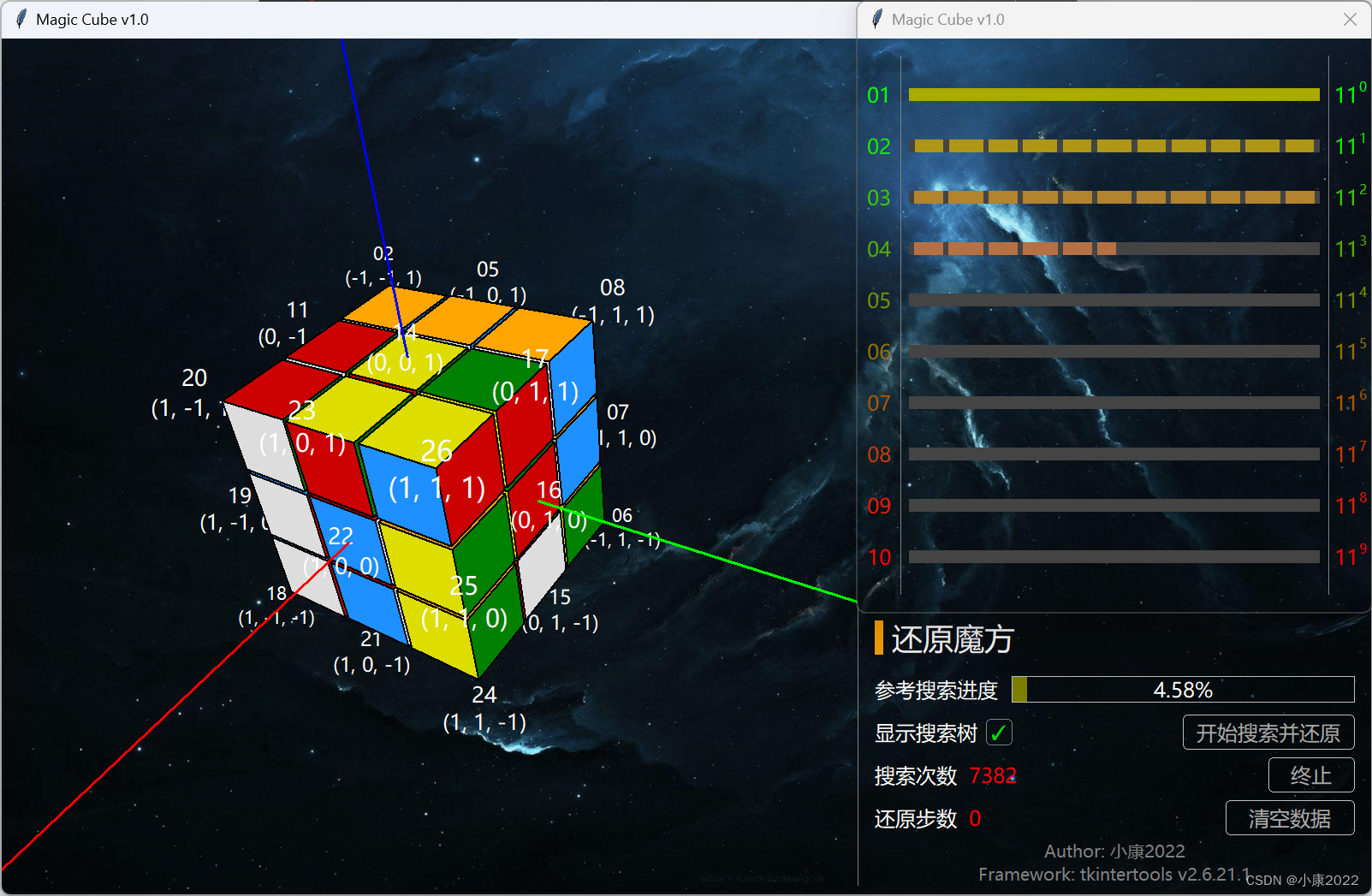

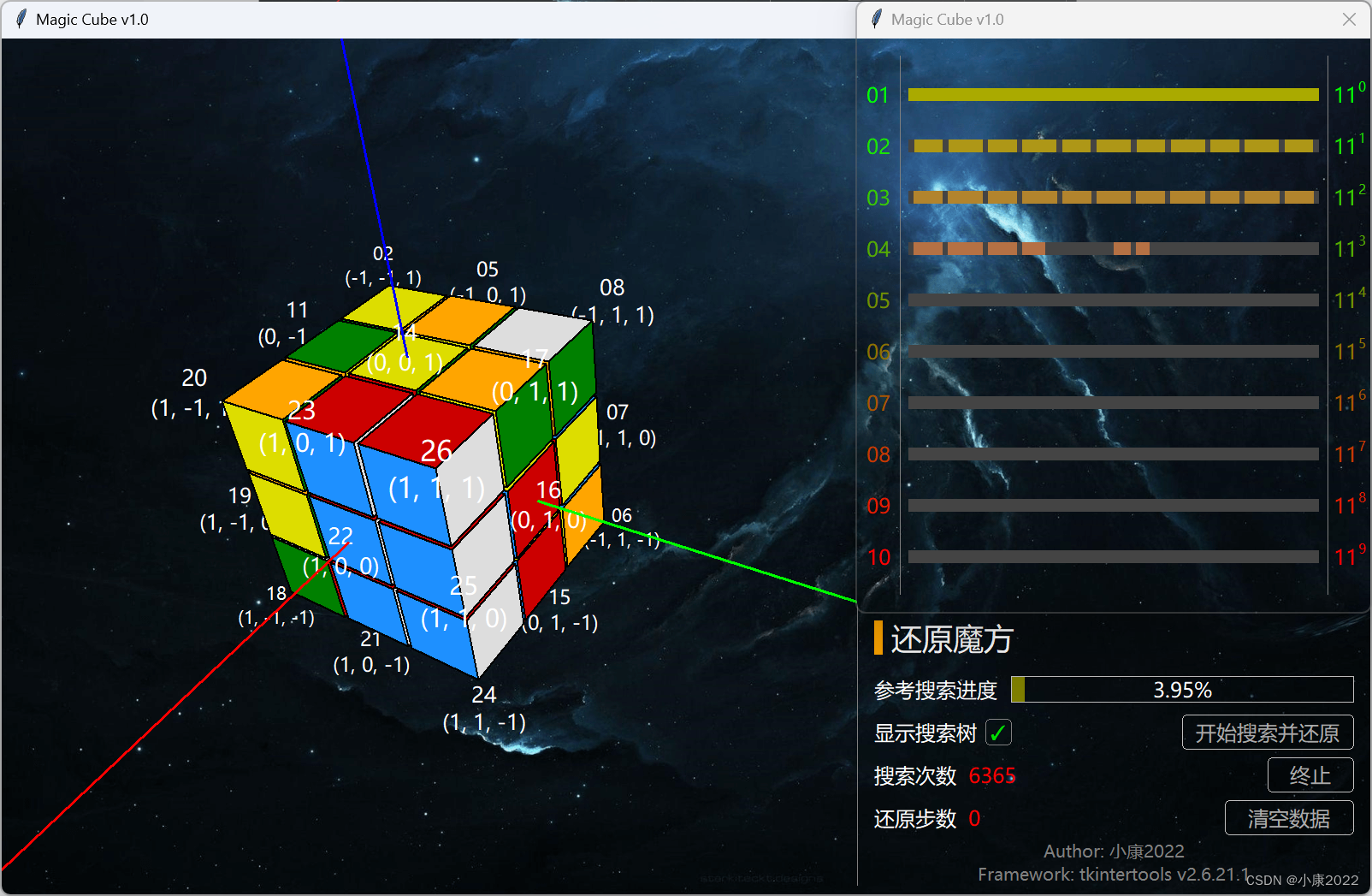

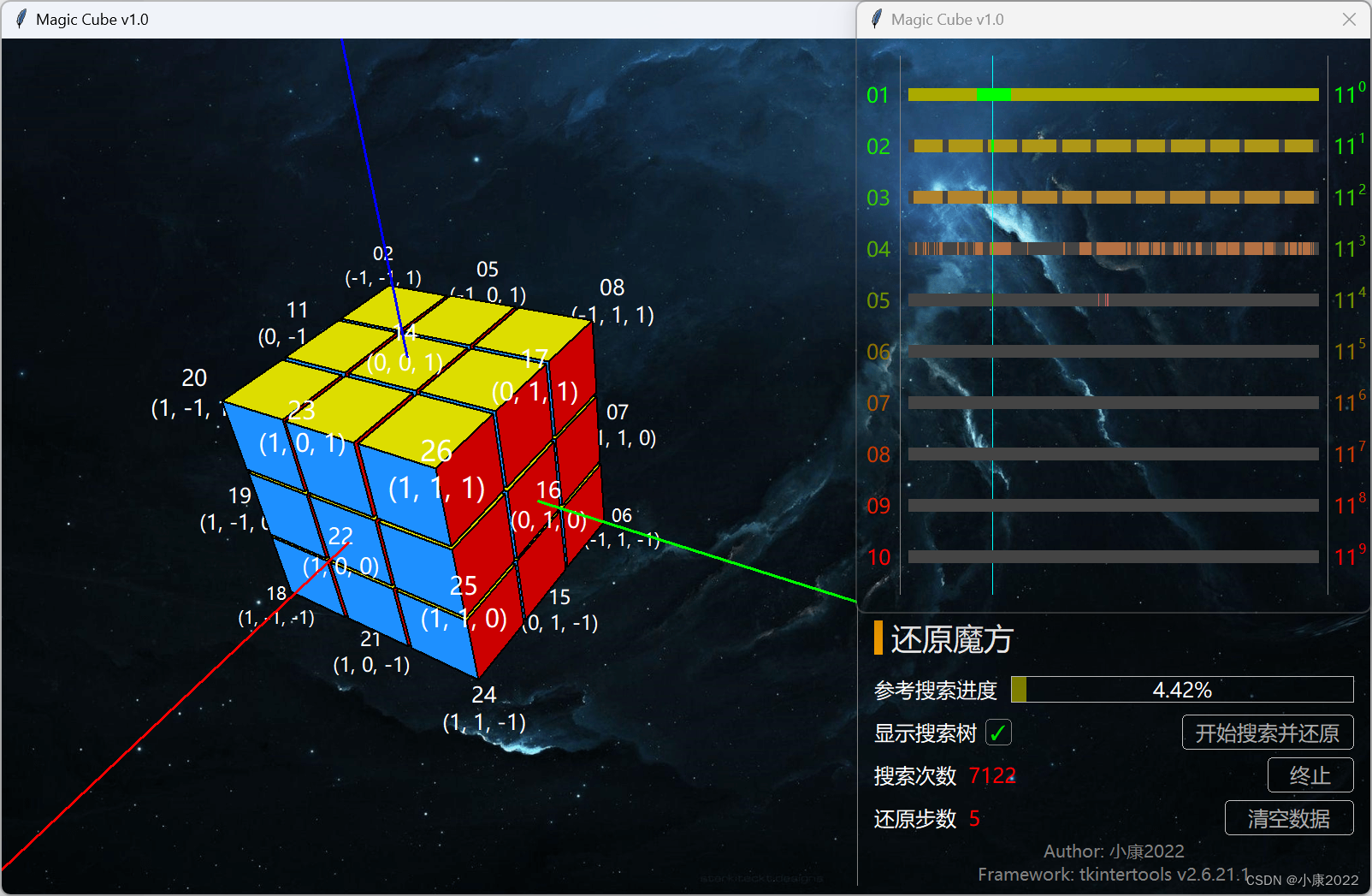
2.3 详细功能
左侧是 3D 显示区,鼠标左键旋转,右键平移,滚轮缩放。
右侧是设定区,点击“开始搜索并还原”时会弹出搜索树弹窗,点击“随机打乱”左边的“/”会弹出“自定义打乱顺序”弹窗。
算法对应表:
| 缩写 | BFS | DFS | UCS | A / A* | HC | REV(测试常用) |
| 说明 | 宽度优先 | 深度优先 | 一致代价优先 | A 或者 A* 算法 | 爬山法 | 不是算法,逆序还原 |
启发函数对应表:
| 缩写 | CBSV | ECLD | MHT | HM | MKWSK | / |
| 说明 | 切比雪夫距离 | 欧几里得距离 | 曼哈顿距离 | 汉明距离 | 闵可夫斯基距离 | h* |
自定义顺序说明:
每个项目由三个部分组成:编号,方向,旋向
方向对应表:
| 缩写 | R | L | U | D | F | B |
| 说明 | 右(Right) | 左(Left) | 上(Up) | 下(Down) | 前(Front) | 后(Back) |
旋向有两个:顺时针和逆时针,对应开关的两种状态
三、实现过程分析
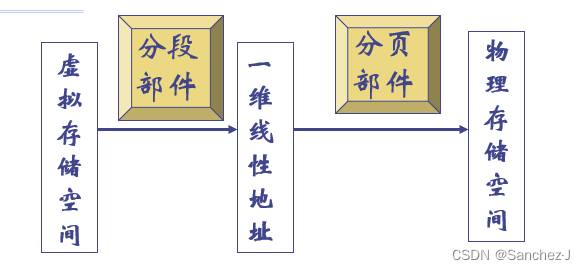
3.1 状态表示
三阶魔方一共有 3³ =27 个方块,于是使用 1×27 大小的数组来表示每个方块的位置,给它们编号 0~26,当编号与其数组索引一致时,表示魔方为还原状态。
当然,由于魔方的特性,这 27 个位置中有些并不会改变。比如,当操作不涉及中转的时候,有 1+1×6 = 7 个方块永远不会改变位置,而当操作涉及中转的时候,只有中心处方块不会改变位置。为了方便表示,仍然采用整个 1×27 大小的数组表示状态。
3.2 操作方式
分两种情况:
- 当不允许三阶魔方中转的时候,操作共有 6×2 = 12 种,即在魔方 6 个面上顺时针旋转 90°或者逆时针旋转 90°。
- 当允许三阶魔方中转的时候,共有 (6+3)×2 = 18 种,即在第一种情况下加上了三个坐标轴垂直的三个中间面的旋转。
当然,经分析,我认为采用第1种情况可能会得到更好结果。
对于第一种情况,魔方将有 1+1×6 = 7 个位置始终固定,使得在完成几乎相同功能的前提下,搜索空间会小一点,且,还原的最终结果只有1个,那就是数组元素与其索引一致。
但反观第二种情况,魔方只有最中间 1 个元素始终固定,在使得搜索空间变大的情况下,还会导致一个程序中不方便处理的问题。因为在这个时候,你会发现,魔方还原的目标状态不只“数组元素与其索引一致”这么一种情况,虽然这可以提高发现目标节点的概率,但搜索空间也变大了,程序实现起来比较麻烦,效率也不见得比第 1 种好。
3.3 启发函数的设计
魔方数据在数组中体现为 1×27,并不方便于直接进行代价的估计,但其在空间上实际是 3×3×3 的,每个方块都有其对应的坐标,于是可以计算每个方块当前位置与目标位置之间的某种差异,并以此作为估计值。
选用的基本启发函数有切比雪夫距离、欧几里得距离、曼哈顿距离和闵可夫斯基距离,同时尝试了一下汉明距离。
不知道什么是切比雪夫距离、欧几里得距离等的朋友,可以去百度一下。
设上述距离对应的启发函数分别为 ![]() 、
、![]() 、
、![]() 、
、![]() 和
和 ![]() 。
。
其中闵可夫斯基距离拥有可调节的参数 p,我这里动态地根据问题的规模大小设计其值。而汉明距离并非一个空间上的关系,它是从数组的数据上直接进行考虑的,即目标数组与当前数组的差异。
对于上述的启发函数,并非所有都满足可纳性。由于魔方转动一次只能转动一个面,也就是说,方块只能在一个面上移动,对于方块,分两种情况:
- 角方块:每次旋转都是沿坐标方向的,对应曼哈顿距离;
- 边方块:每次旋转都是沿斜直线方向,对应欧几里得距离;
- 面中心方块:始终没有任何移动,计算时不考虑它。
每个面上角方块与边方块各占一半,故 ![]() ,但是有:
,但是有:
![]()
因此有:
![]()
已知,对于闵可夫斯基距离,参数 p=1 时,![]() ,参数 p=2 时,
,参数 p=2 时,![]() ,参数 p=+∞ 时,
,参数 p=+∞ 时,![]() ,可通过调控其参数 p 来控制其最终效果。
,可通过调控其参数 p 来控制其最终效果。
汉明距离并非空间上的距离,属于抽象距离,无法与上面的进行比较。
综上,启发函数为切比雪夫距离、欧几里得距离时,算法为 A* 算法,曼哈顿距离对应的为 A 算法,闵可夫斯基距离是否为 A* 算法与参数 p 有关,汉明距离对应的暂时无法确定。
3.4 算法实现
BFS:用队列实现
DFS:用堆栈实现
UCS:用优先级队列实现,评估函数 F = 代价函数 G
A/A*:用优先级队列实现,评估函数 F = 代价函数 G + 启发函数 H
HC:用优先级队列实现,评估函数 F = 启发函数 H
3.5 结果显示方法
结果采用三种方式进行可视化。
- 搜索之前的打乱魔方与搜索之后的还原魔方通过 3D 魔方实时演示旋转过程;
- 搜索过程之中,通过进度条得知总搜索空间的大小以及当前搜索的空间大小,直观显示其百分占比,并实时显示搜索次数,搜索完成后显示还原步骤的数量;
- 搜索过程中实时展示搜索树,由于此数的每层节点数量是指数级增长的,于是就需要将其对数化后以线性的方式的进行展示,层数越大,颜色越深,搜索完毕后标识出搜索路径。
这里说一下为什么实际搜索的状态空间是 11 的 n 次方,而不是 12 的 n 次方,因为每次操作,虽然有 12 步,但实际我们手动不允许它执行与上次转动相反的操作,因为你顺时针转一下,再逆时针转一下,那不等于没转吗?
别小看这点优化,11⁶ = 1771561,12⁶ = 2985984,仅 6 步,相差多少自己看看。
四、写在后面
4.1 开源图形库
本程序使用的 tkintertools 是我自己一个人开发的图形界面库,基于 tkinter,实现了一些 tkinter 没有的功能,里面还有一个可以称为“微型 3D 引擎”的子模块,上述 3D 效果就是这样实现的,此外还提供了较为强大的动画能力,希望大家能支持一下下!
GitHub repo:GitHub - Xiaokang2022/tkintertools
github.io: Profile - 简介 - tkintertools (xiaokang2022.github.io)
4.2 源代码下载
链接文件包含了源代码,以及已经打包好,可以直接运行的 exe 文件。
源代码及打包程序下载链接:Magic Cube.zip - 蓝奏云
记得给我点赞!收藏!以及在评论区留下你的足迹呀!