a = 2; b = 5;
x = 0:pi/40:pi/2; %增量为pi/40
y = b*exp(-a*x).*sin(b*x).*(0.012*x.^4-0.15*x.^3+0.075*x.^2+2.5*x); %点乘的意义
z = y.^2; %点乘的意义
w(:,1) = x; %组成w,第一列为x
w(:,2) = y; %组成w,第二列为y
w(:,3) = z; %组成w,第三列为z
format short g; %短格式显示
w %不加分号,显示数据
%绘图显示,注意各种符号的属性设置
plot(x,y,'--rp','LineWidth',1.5,'MarkerSize',15,'MarkerEdgeColor','r','MarkerFaceColor','w');
hold on
plot(x,z,'b-s','MarkerEdgeColor','b','MarkerFaceColor','g');
legend('y关于x曲线','z关于y的曲线');

clc,clear;
q0 = 10; R = 60; C = 0.00005; t = linspace(0,0.8,100);
styleline = {'r-','b--','m:','c-.'};
leg = {};
i = 1; Qtl(1,:) = t;
for L = 3:3:12
qt = q0*exp(-R*t/2/L).*cos(sqrt(1/L/C-(R/2/L)^2).*t);
Qtl(i+1,:) = qt;
plot(Qtl(1,:),Qtl(i+1,:),styleline{i});
plot(t,qt,styleline{i},'LineWidth',2);
leg{i} = strcat('L = ', num2str(L));
i = i + 1;
hold on
end
title('电量随时间的变化曲线');
legend(leg,'location','best');
xlabel('t(s)');
ylabel('q(t)');
grid on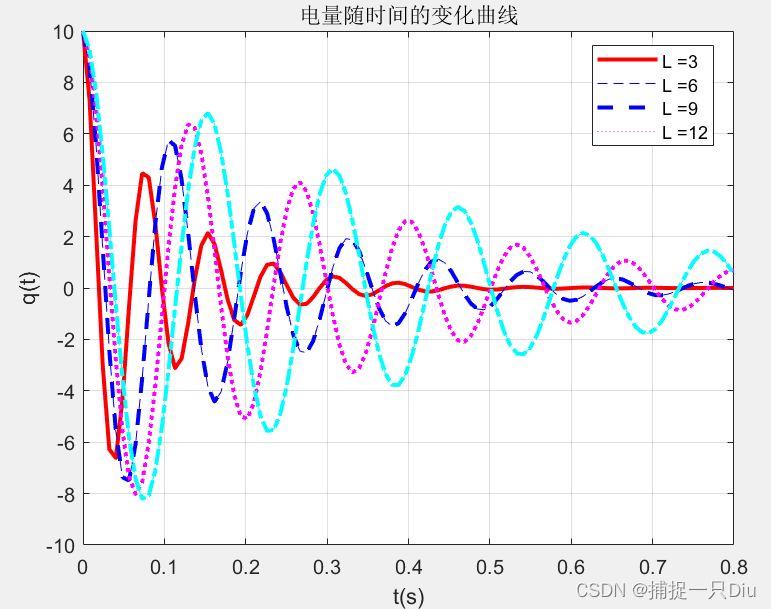

%按要求处理第(1)步
x=0:pi/100:3*pi;
y=sin(x);
y1=(y>=0).*y; %消去负半波
p=sin(pi/3);
%按要求处理第(2)步
y2=(y>=p)*p+(y<p).*y1;
plot(x,y,'r-','LineWidth',2)
hold on;
grid on
plot(x,y2,'b-','LineWidth',2)
例4:元胞数组示例
x = 0:pi/100:2*pi; %x从[0, 2pi]之间等分100份
y(1,:) = x.*sin(x); %第一个函数,且计算值
y(2,:) = x.^2-4*x-4;
y(3,:) = x.*cos(x);
y(4,:) = x.*log(x);
colors = {'r','b','g','m'}; %颜色元胞数组
linestype = {'-','--',':','-.'}; %线形元胞数组
led = {'x.*sin(x)','x.^2-4*x-4','x.*cos(x)','x.*log(x)'}; %图例元胞数组
for i = 1:4 %循环绘制4条曲线
plot(x,y(i,:),strcat(colors{i},linestype{i}),'LineWidth',2);
hold on
end
legend(led,'Location','best') %添加图例
grid on;
hold off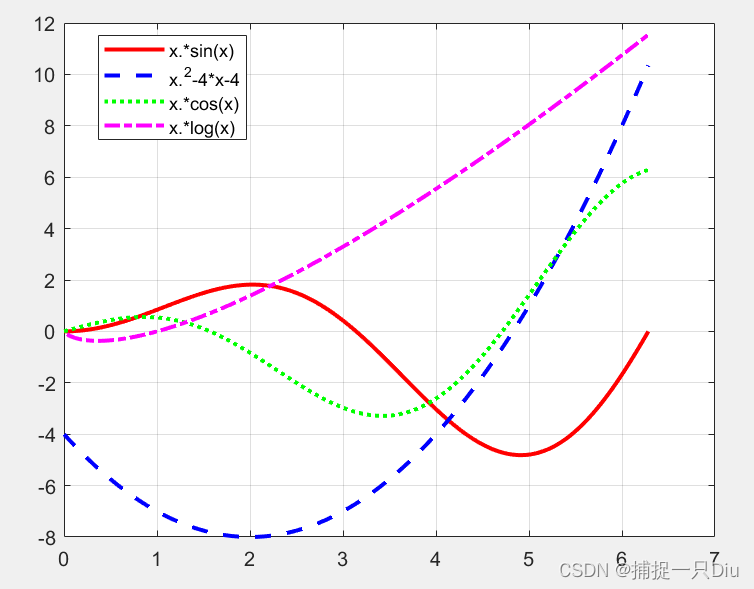
例5. 方向余弦矩阵(DCM, Direction Consine Matrix)

例6. 计算平行六面体的体积

例7. 用Cramer法则求解线性方程组
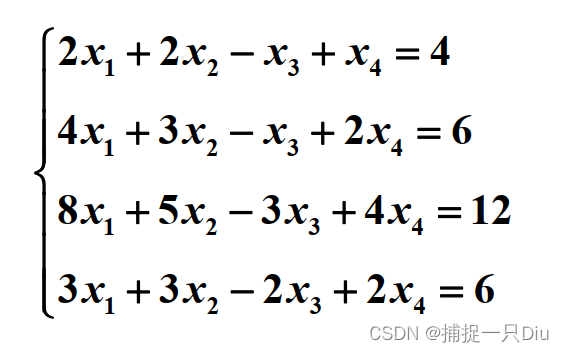
clc, clear
D = [2, 2, -1, 1; 4, 3, -1, 2; 8, 5, -3, 4; 3, 3, -2, 2];
b = [4; 6; 12; 6];
D1 = [b, D(:, 2:4)];
D2 = [D(:, 1:1), b, D(:, 3:4)];
D3 = [D(:, 1:2), b, D(:, 4:4)];
D4 = [D(:, 1:3), b];
DD = det(D);
x1 = det(D1) / DD;
x2 = det(D2) / DD;
x3 = det(D3) / DD;
x4 = det(D4) / DD;
X = [x1, x2, x3, x4]
% X = [1, 1, -1, -1]
Cramer(D, b)function Cramer(A, b)
%% 1、输入参数的判断
if nargin == 0 || nargin == 1
disp('您输入的参数个数不足!');
return
end
%% 2、判断是否为方阵
[rs, cs] = size(A);
if rs ~= cs
disp('系数矩阵必须是方阵,否则无法用Cramer法则求解!');
return
end
%% 3、求解判断系数矩阵行列式的值
D = det(A);
if D == 0
disp('系数矩阵行列式等于0!');
return
end
%% 4、用Cramer法则求解和输出
disp('线性方程组的解为:');
for i = 1:rs
AX = [A(:, 1:i-1), b, A(:, i+1:cs)];
x = det(AX) / D;
fprintf('x%d = %.6f\n', i, x)
end
end
例8. 矩阵分解
clc, clear
%% 对称正定矩阵的三角分解——Cholesky分解
A = gallery('lehmer', 5) % 生成正定矩阵
L = chol(A)
L'*L
% A = L' * L
norm(A - L' * L, 'fro')
%% 实对称矩阵的QDQ分解
B = gallery('fiedler', 5) % 生成对称矩阵
[V, D] = eig(B)
V*D*V'
norm(V*D*V' - B, 'fro')
%% LU分解
%[𝑳, 𝑼, 𝑷] = 𝒍𝒖(𝑨): 𝑷𝑨 = 𝑳𝑼
[L, U, P] = lu(A)
A = [2 5 4 1;1 3 2 1;2 10 9 7;3 8 9 2];
b = [20 11 40 37]';
[L, U, P] = lu(A)
Y = inv(L)*P*b
X = inv(U)*Y
X1 = A\b
%% QR分解
A = magic(5)
[Q, R] = qr(A)
Q*R
%% 奇异值分解
A = round(5*randn(5, 4))
s = svd(A) % s = svd(A) 以降序顺序返回矩阵 A 的奇异值。
[U, S, V] = svd(A)
B = A'*A;
D = eig(B);
sqrt(D)
例9. 线性方程组求解
function [x, y] = leqsolve(A, b)
%% 求解线性方程组的解,
% 输入参数:A系数矩阵,b是右端向量,
% 输出参数:x是唯一解或特解,y是基础解系
if nargin < 2
disp('请您输入系数矩阵A和右端向量b!')
return
end
y = []; % 基础解系
[m, n] = size(A); % 系数矩阵维度的长度
if norm(b) > 0 % 非齐次方程
if rank(A) == rank([A, b]) % 方程组相容,有解
if rank(A) == n % 唯一解
disp('方程组有唯一解:')
x = A\b;
else % 方程有无穷多个解,基础解系
disp('方程组有无穷多个解,其齐次方程组的基础解系是y,特解是x:')
x = A\b; % 特解
y = null(A, 'r'); % 基础解系
end
else % 方程组不相容,给出最小二乘解
disp('方程组最小二乘解是:')
x = A\b;
end
else % 齐次方程
if rank(A) >= n % 列满秩
x = zeros(n, 1); % 零解
else % 非零解
disp('方程组有无穷多个解,基础解系x是:')
x = null(A, 'r');
end
end
end