一、题目
纸牌三角形(难度:★★★)
A,2,3,4,5,6,7,8,9 共9张纸牌排成一个正三角形(A按1计算)。要求每个边的和相等。
下图就是一种排法。
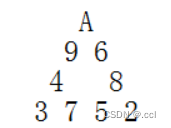
这样的排法可能会有很多。
如果考虑旋转、镜像后相同的算同一种,一共有多少种不同的排法呢?
请你计算并提交该数字。
二、代码
package Lan2017;
public class B纸牌三角形 {
/*纸牌三角形
A,2,3,4,5,6,7,8,9 共9张纸牌排成一个正三角形(A按1计算)。要求每个边的和相等。
下图就是一种排法(
A
9 6
4 8
3 7 5 2
这样的排法可能会有很多。
如果考虑旋转、镜像后相同的算同一种,一共有多少种不同的排法呢?
请你计算并提交该数字。
注意:需要提交的是一个整数,不要提交任何多余内容。*/
/*
* 思路:
* 我们肯定是要遍历找出这九张牌的位置,采用深度优先遍历的算法*/
//把这九个数存放在数组中,定义为 static,可以被实例共享
static int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9};
static int count = 0;
//main
public static void main(String args[]) {
dfs(0);
System.out.println(count / 6);
}
//dfs
static void dfs(int m) {
if (m >= 9) {
if (arr[0] + arr[1] + arr[2] + arr[3] == arr[3] + arr[4] + arr[5] + arr[6] && arr[3] + arr[4] + arr[5] + arr[6] == arr[6] + arr[7] + arr[8] + arr[0]){
count++;
}
return;
}
for(int i = m; i < 9; i++) {
swap(m, i);
dfs(m + 1);
swap(m, i);
}
}
static void swap(int i,int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
三、反思
1.为啥要count除以6,这是因为要考虑到旋转和镜像后的算一种,
有这六种:
| 原本的三角形 | 顺时针转120度 | 逆时针转120度 | 垂直镜像 | 水平镜像 | 对角线镜像 |
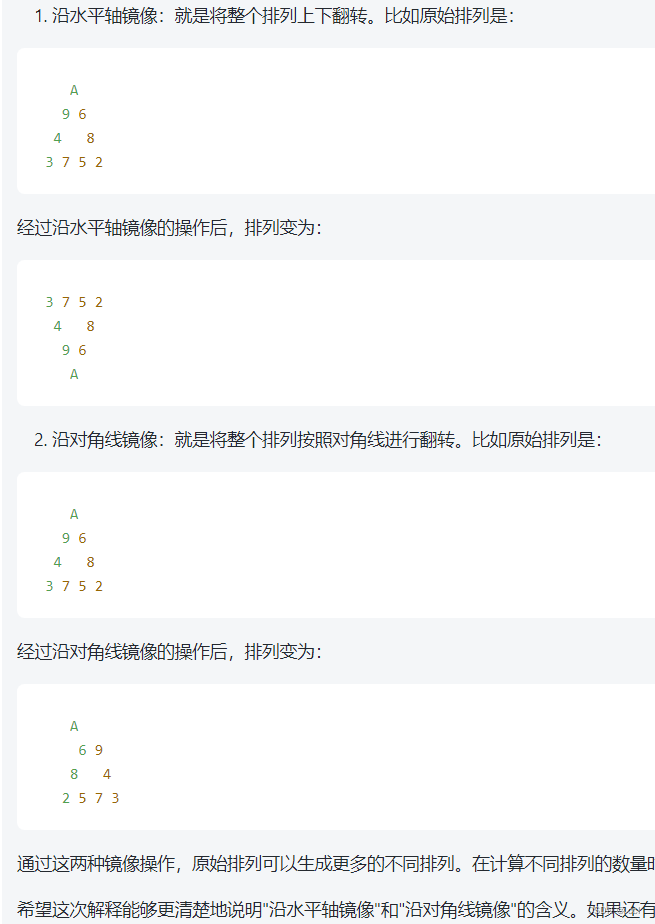
2.对于return的理解,就是 当我们找到了满足的三角形,我们结束当前的深度优先搜索,避免一些无用的组合,浪费我们的时间。