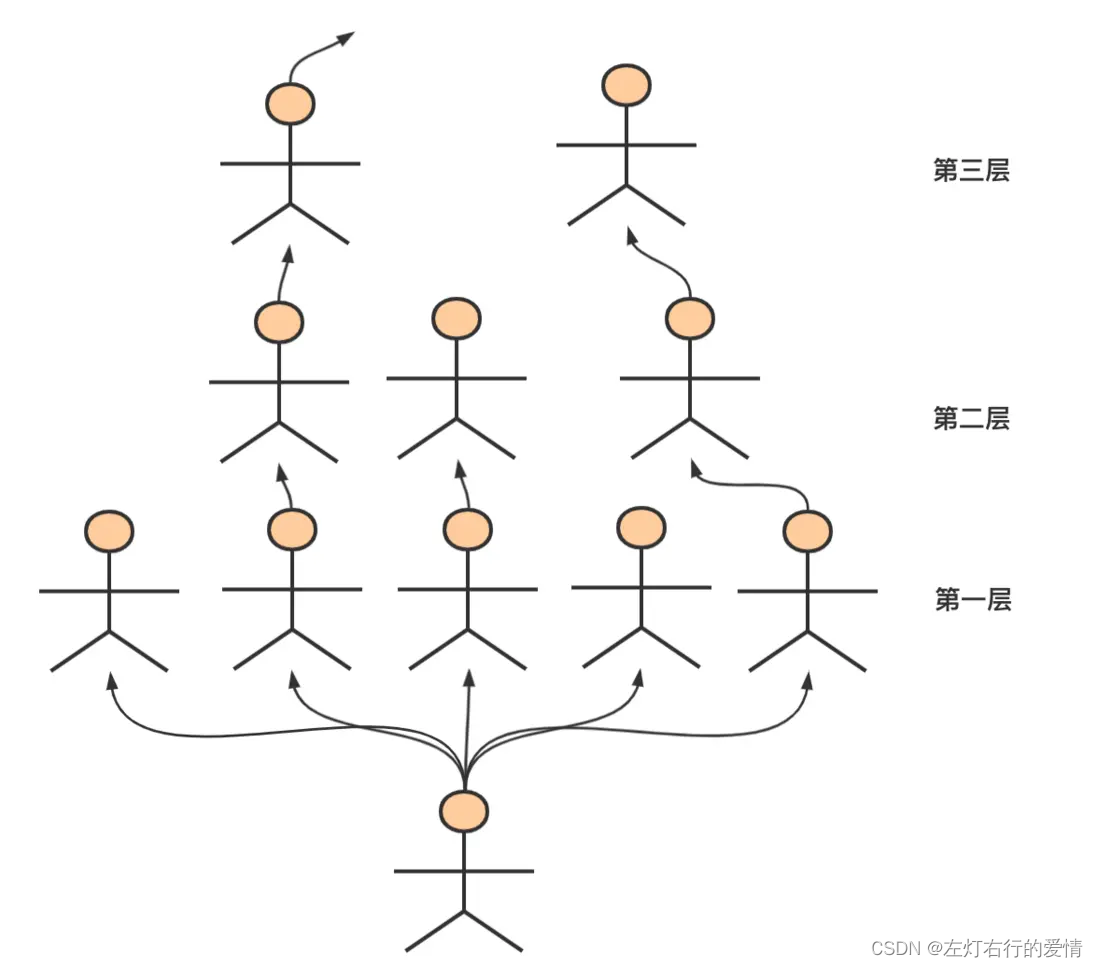
其实就是将搜索过程一些不必要的部分直接剔除掉。
剪枝是回溯法的一种重要优化手段，往往需要先写一个暴力搜索，然后找到某些特殊的数学关系，或者逻辑关系，通过它们的约>束让搜索树尽可能浅而小，从而达到降低时间复杂度的目的。

示例：

分析：
n->[1,10]，数据范围并不是很大，我们可以考虑枚举所有答案来找到这个最合适的队伍数量。
就比如说，我现在有n个人，那么最多的队伍数量肯定不超过n，所以我们可以从只有1个队伍枚举到有n个队伍，肯定能找到其中一种方案符合题意。当时由于一个队伍中不能有处于倍数关系的整数，所以我们可以使用剪枝做优化，在一开始就判断，如果不符合题意就排除掉，提高效率。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
int n;
int a[N];
vector<int> v[N];
int dfs(int cnt,int dep){
	if(dep==n+1){
		return true;
	}
	
	for(int i=1;i<=cnt;i++){
		bool tag=true;
		for(const auto&j:v[i]){
			if(a[dep]%j==0){
				tag=false;break;	
			}
		}
		if(!tag)continue;
		v[i].push_back(a[dep]);
		if(dfs(cnt,dep+1))return true;
		//恢复现场 
		v[i].pop_back();
	}
	return false;
}
int main(){
	ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i];
	
	for(int i=1;i<=n;i++){
		if(dfs(i,1)){ //有i个队伍，第1层出发 
			cout<<i<<'\n';
			break;
		}
	}
	return 0;
}