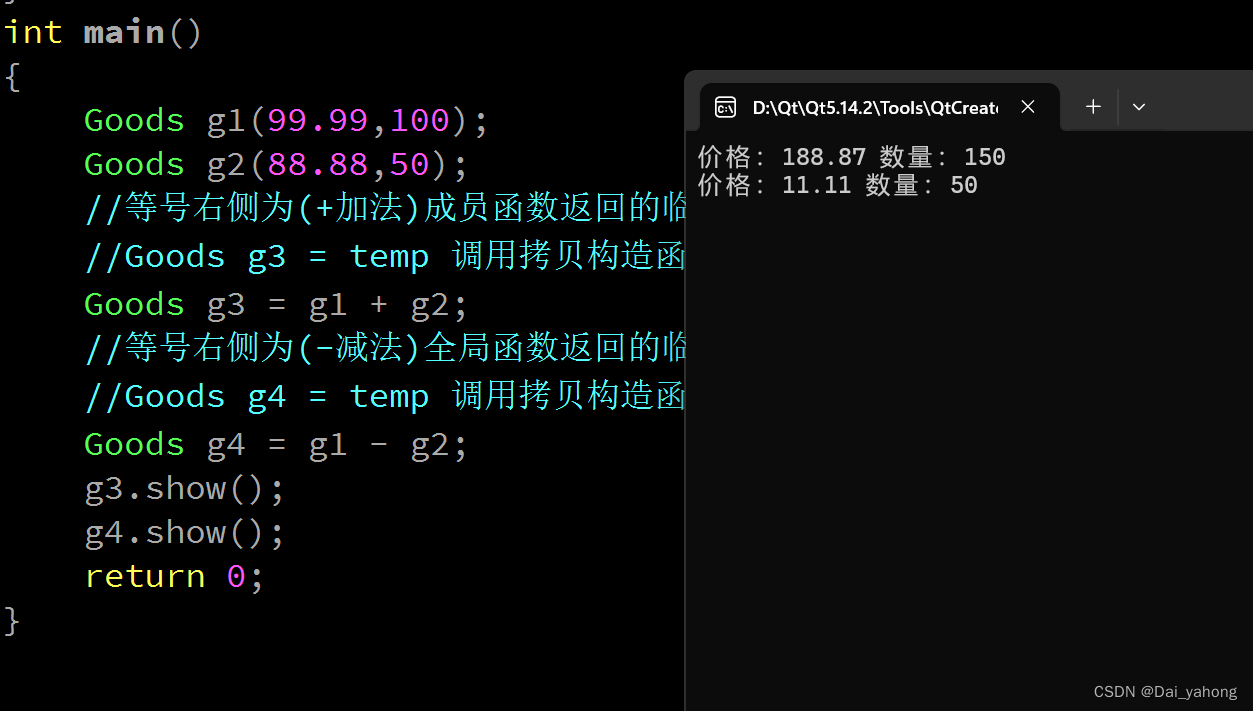
一、封装类 用其成员函数实现(对该类的)数学运算符的重载(加法),并封装一个全局函数实现(对该类的)数学运算符的重载(减法)。
代码:
#include <iostream>
using namespace std;
//封装 货物Goods 类
class Goods
{
//把全局函数设置为类的友元 方便访问私有成员进行运算
friend const Goods operator-(const Goods &L,const Goods &R);
private:
double price;//价格
int num;//数量
public:
Goods() {}//无参构造函数
//有参构造函数
Goods(double p,int m):price(p),num(m)
{}
//运算符重定义成员函数 实现+加法;
const Goods operator+(const Goods &R)const
{
//定义临时类变量 存储计算后的结果并返回
Goods temp;
temp.price = price + R.price;
temp.num = num + R.num;
return temp;
}
void show()
{
cout << "价格:" << price << " 数量:" << num << endl;
}
};
//封装运算符重定义一般函数 实现-减法;
const Goods operator-(const Goods &L,const Goods &R)
{
//临时的类变量 存储计算结果并返回
Goods temp;
temp.price = L.price - R.price;
temp.num = L.num - R.num;
return temp;
}
int main()
{
Goods g1(99.99,100);
Goods g2(88.88,50);
//等号右侧为(+加法)成员函数返回的临时值 Goods temp
//Goods g3 = temp 调用拷贝构造函数完成初始化;
Goods g3 = g1 + g2;
//等号右侧为(-减法)全局函数返回的临时值 Goods temp
//Goods g4 = temp 调用拷贝构造函数完成初始化;
Goods g4 = g1 - g2;
g3.show();
g4.show();
return 0;
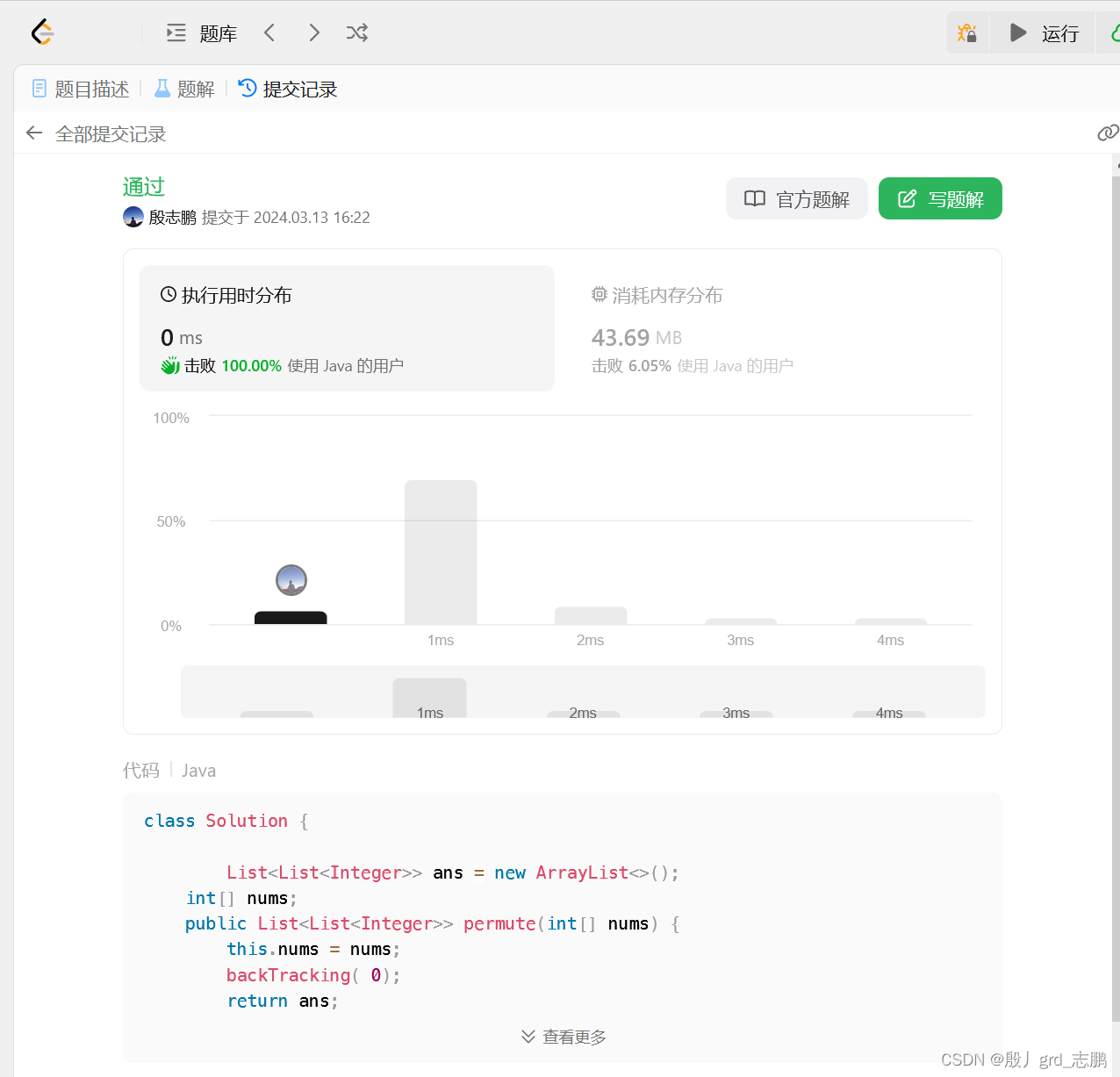
}运行:
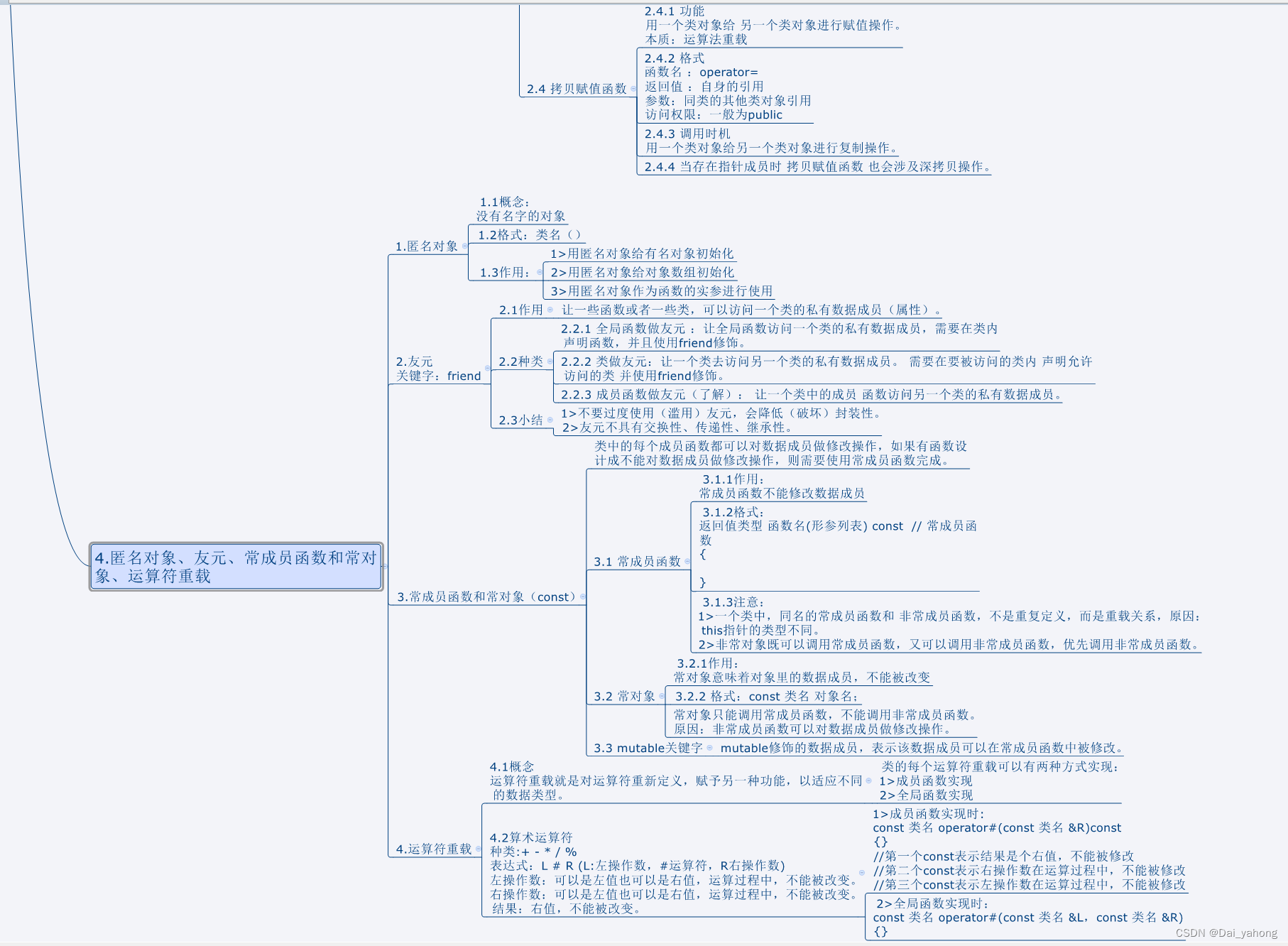
思维导图