---

1.背景

2022年，Braik 等人受到白鲨捕食行为启发，提出了非洲秃鹫优化算法(White Shark Optimizer, WSO)。

2.算法原理

2.1算法思想

海洋中白鲨拥有敏锐的感知、听觉和嗅觉，WSO模拟了白鲨探索整个搜索空间来追踪、定位和捕获猎物,并通过白鲨位置的不断更新来达到求解优化问题。

2.2算法过程

速度更新:
这里很像PSO更新方式，作者对控制参数进行了更为复杂的设置。
$$v_{k+1}^i=\mu [v_k^i+p_1\left(w_{{\text{gbest }}_k}-w_k^i\right)\times c_1+p_2\left(w_{\text{best}}^{v_k^i}-w_k^i\right)\times c_2]$$
其中，参数$p_1,p_2$表述如下：
$$\begin{array}{rl}{p}_1& =p_{max}+(p_{max}-p_{min})\times e^{-(4k/K{)}^2}\\ p_2& =p_{min}+(p_{max}-p_{min})\times e^{-(4k/K{)}^2}\end{array}$$
位置更新：
大白鲨常常在不断寻找潜在猎物，可能位于最佳或次优位置。它们会通过听到猎物移动引起的波浪声或闻到猎物的气味来确定位置。
$$w_{k+1}^i=\{\begin{array}{cc}{w}_k^i\cdot \neg \oplus w_o+u\cdot a+l\cdot b& R<m_v\\ w_k^i+v_k^i/f& R⩾m_v\end{array}$$
其中， $\neg ,\oplus$分别为否定运算和异或运算。其余参数表述为：
$$\begin{gathered} a=\mathrm{sgn}(w_k^i-u)>0 \\ b=\mathrm{sgn}(w_k^i-l)<0 \\ {w}_o=\oplus (a,b) \end{gathered}$$
向猎物移动：
$$w_{k+1}^i=w_{g{\text{best}}_k}+r_1{\vec{D}}_w\text{sgn}(r_2-0.5)r_3<s_s$$
最优解保留：
$$w_{k+1}^i=\frac{w_k^i+w_{k+1}^i}{2\times R}$$
伪代码：

3.代码实现

% 白鲨优化算法
function [Best_pos, Best_fitness, Iter_curve, History_pos, History_best] = WSO(pop, maxIter, lb, ub, dim,fobj)
%input
%pop 种群数量
%dim 问题维数
%ub 变量上边界
%lb 变量下边界
%fobj 适应度函数
%maxIter 最大迭代次数
%output
%Best_pos 最优位置
%Best_fitness 最优适应度值
%Iter_curve 每代最优适应度值
%History_pos 每代种群位置
%History_best 每代最优个体位置
%% Convergence curve
Iter_curve=zeros(1,maxIter);
%% 初始化
WSO_Positions = zeros(pop, dim);
for i = 1:pop
    for j = 1:dim
        WSO_Positions(i,j) = (ub(j) - lb(j)) * rand() + lb(j);
    end
end
% initial velocity
v=0.0*WSO_Positions; 
%% 计算适应度
fit=zeros(pop,1);
for i=1:pop
     fit(i,1)=fobj(WSO_Positions(i,:));
end

%% 记录
fitness=fit; % Initial fitness of the random positions of the WSO
[Best_fitness,index]=min(fit);

wbest = WSO_Positions; % Best position initialization
Best_pos = WSO_Positions(index,:); % initial global position

%% WSO Parameters
    fmax=0.75; %  Maximum frequency of the wavy motion
    fmin=0.07; %  Minimum frequency of the wavy motion   
    tau=4.11;  
       
    mu=2/abs(2-tau-sqrt(tau^2-4*tau));

    pmin=0.5;
    pmax=1.5;
    a0=6.250;  
    a1=100;
    a2=0.0005;
%% 迭代 
for ite=1:maxIter

    mv=1/(a0+exp((maxIter/2.0-ite)/a1)); 
    s_s=abs((1-exp(-a2*ite/maxIter))) ;
 
    p1=pmax+(pmax-pmin)*exp(-(4*ite/maxIter)^2);
    p2=pmin+(pmax-pmin)*exp(-(4*ite/maxIter)^2);
    
 %% Update the speed of the white sharks in water  
     nu=floor((pop).*rand(1,pop))+1;

     for i=1:size(WSO_Positions,1)
           rmin=1; rmax=3.0;
          rr=rmin+rand()*(rmax-rmin);
          wr=abs(((2*rand()) - (1*rand()+rand()))/rr);       
          v(i,:)=  mu*v(i,:) +  wr *(wbest(nu(i),:)-WSO_Positions(i,:));
           %% or                

%          v(i,:)=  mu*(v(i,:)+ p1*(gbest-WSO_Positions(i,:))*rand+.... 
%                    + p2*(wbest(nu(i),:)-WSO_Positions(i,:))*rand);          
     end
 
 %% Update the white shark position
     for i=1:size(WSO_Positions,1)
       
        f =fmin+(fmax-fmin)/(fmax+fmin);
         
        a=sign(WSO_Positions(i,:)-ub)>0;
        b=sign(WSO_Positions(i,:)-lb)<0;
         
        wo=xor(a,b);

        % locate the prey based on its sensing (sound, waves)
            if rand<mv
                WSO_Positions(i,:)=  WSO_Positions(i,:).*(~wo) + (ub.*a+lb.*b); % random allocation  
            else   
                WSO_Positions(i,:) = WSO_Positions(i,:)+ v(i,:)/f;  % based on the wavy motion
            end
    end 
    
    %% Update the position of white sharks consides_sng fishing school 
for i=1:size(WSO_Positions,1)
        for j=1:size(WSO_Positions,2)
            if rand<s_s      
                
             Dist=abs(rand*(Best_pos(j)-1*WSO_Positions(i,j)));
             
                if(i==1)
                    WSO_Positions(i,j)=Best_pos(j)+rand*Dist*sign(rand-0.5);
                else    
                    WSO_Pos(i,j)= Best_pos(j)+rand*Dist*sign(rand-0.5);
                    WSO_Positions(i,j)=(WSO_Pos(i,j)+WSO_Positions(i-1,j))/2*rand;
                end   
            end
         
        end       
end
%     

%% Update global, best and new positions
 
    for i=1:pop 
        % Handling boundary violations
           if WSO_Positions(i,:)>=lb & WSO_Positions(i,:)<=ub%         
            % Find the fitness
              fit(i)=fobj(WSO_Positions(i,:));    
              
             % Evaluate the fitness
            if fit(i)<fitness(i)
                 wbest(i,:) = WSO_Positions(i,:); % Update the best positions
                 fitness(i)=fit(i);   % Update the fitness
            end
            
            %% Finding out the best positions
            if (fitness(i)<Best_fitness)
               Best_fitness=fitness(i);
               Best_pos = wbest(index,:); % Update the global best positions
            end 
            
        end
    end
    Iter_curve(ite) = Best_fitness;
    History_pos{ite} = WSO_Positions;
    History_best{ite} = Best_pos;
end 
end

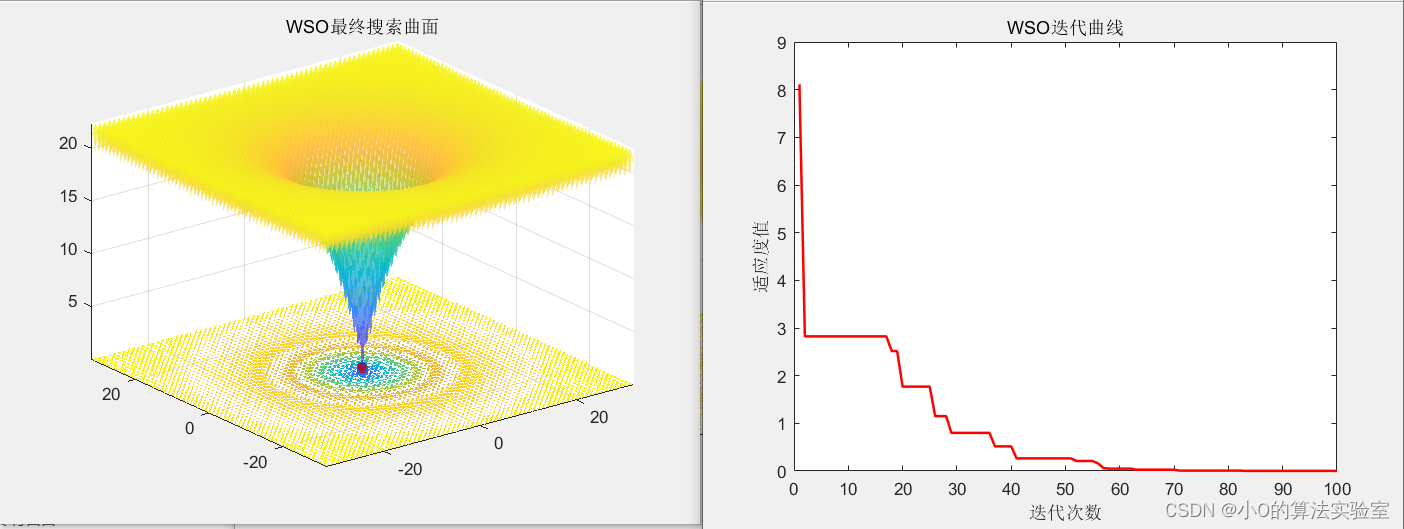
4.参考文献

[1] Braik M, Hammouri A, Atwan J, et al. White Shark Optimizer: A novel bio-inspired meta-heuristic algorithm for global optimization problems[J]. Knowledge-Based Systems, 2022, 243: 108457.