1.7 什么是可变形卷积？可变形卷积旨在解决哪类问题？

news2024/9/27 19:22:52

1.7 什么是可变形卷积？可变形卷积旨在解决哪类问题？

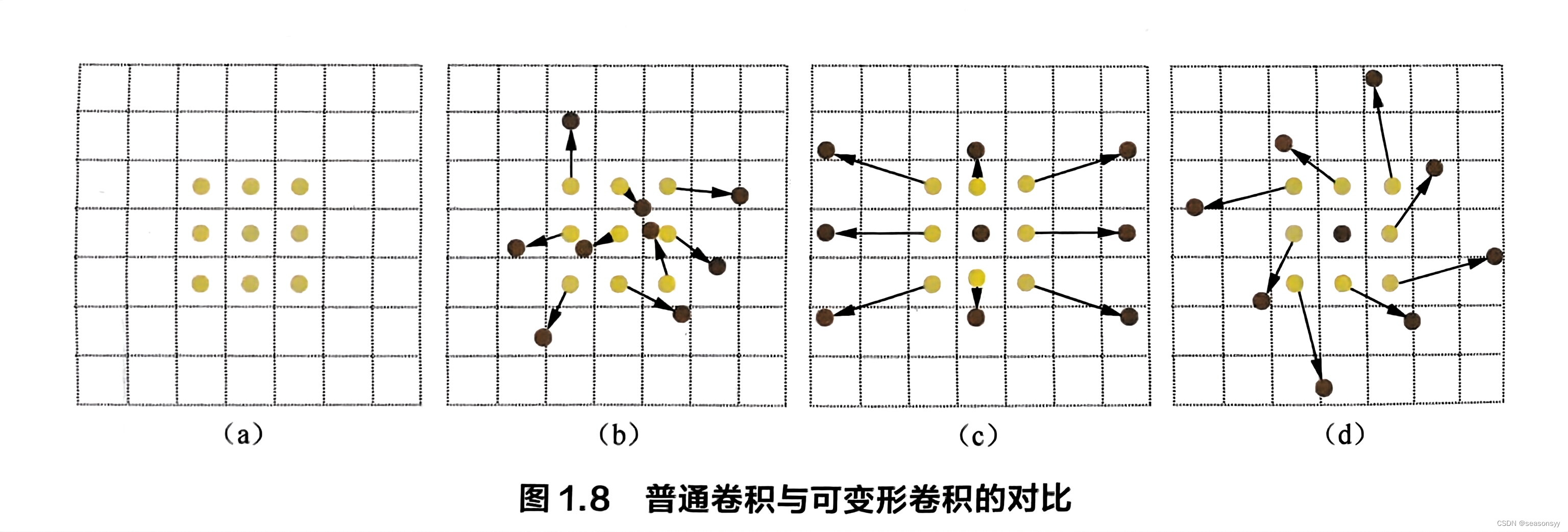
问题：深度卷积神经网络在许多视觉任务上获得了重大突破，其强大的特征提取能力避免了传统的人工特征工程的弊端。然而，普通的卷积操作是在固定的、规则的网格点上进行数据采样，如图1.8(a) 所示，这束缚了网络的感受野形状，限制了网络对几何形变的适应能力。

1.可变形卷积

解决：为了克服这个限制，可变形卷积在卷积核的每个采样点上添加一个可学习的偏移量(offset)，让采样点不再局限于规则的网格点，如图1.8(b)所示。

图1.8（c）和图1.8（d）可变形卷积的两个特例：
- 图1.8（c）在水平方向上对卷积核有较大拉伸，体现了可变形卷积的尺度变换特性；
- 图1.8（d）则是对卷积核进行旋转。
特别地，图1.8©中的可变形卷积核有点类似于空洞卷积；

实际上，空洞卷积可以看作一种特殊的可变形卷积。

空洞卷积详见以下链接：
https://blog.csdn.net/seasonsyy/article/details/136629145?spm=1001.2014.3001.5501

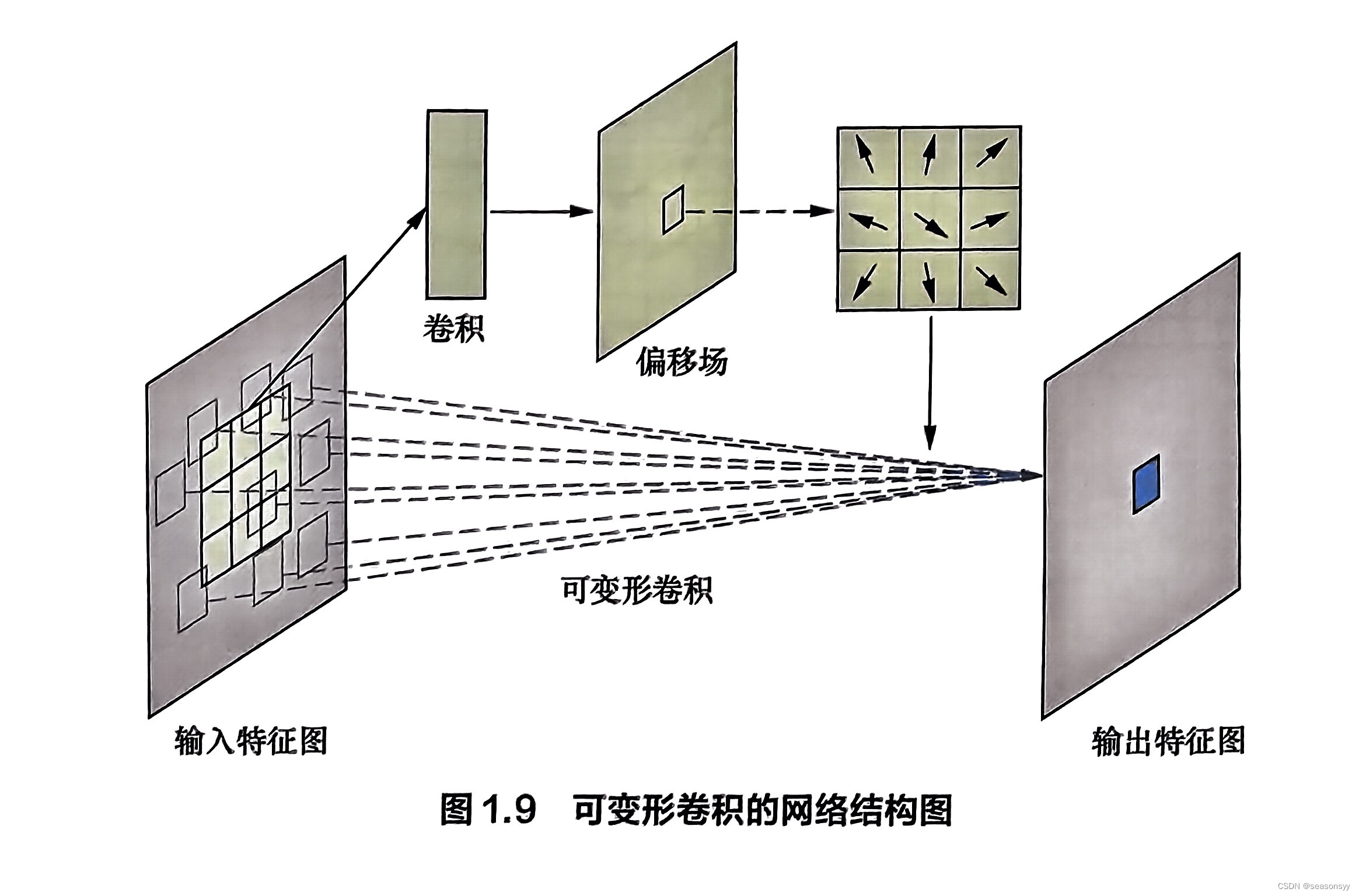
在这里插入图片描述

可变形卷积让网络具有了学习空间几何形变的能力。具体来说，可变形卷积引入了一个平行分支来端到端地学习卷积核采样点的位置偏移量，如图1.9所示。该平行分支先根据输入特征图计算出采样点的偏移量，然后再在输入特征图上采样对应的点进行卷积运算。这种结构让可变形卷积的采样点能根据当前图像的内容进行自适应调整。

在这里插入图片描述

2.可变形卷积计算过程

我们以二维卷积为例，详细说明可变形卷积的计算过程。

假设卷积核尺寸为3×3,记R ={(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1)},它对应着卷积核的9个采样点。首先来看普通卷积，它可以用公式形式化为

$y({p_0}) = \sum\limits_{{p_n} \in R} {w({p_n}) \cdot x({p_0} + {p_n})}$

其中，x(·)和y(·)分别是卷积层的输入特征图和输出特征图，p₀是滑动窗的中心点，pn是卷积核的采样点。

对于可变形卷积，它的计算公式则是
$y({p_0}) = \sum\limits_{{p_n} \in R} {w({p_n}) \cdot x({p_0} + {p_n} + \Delta {p_n})}$

- 其中，△pn是采样点的位置偏移量。由于△pn是在网络中端到端地学习得到的，它可能不是整数，这会导致不在整数网格点上，此时需要采用双线性插值：

$\sum\limits_q {G(q,p) \cdot x(q)}$

其中，p是任意位置点，例如取 ${p_0} + {p_n} + \Delta {p_n}$ ，q是整数网格点，

$\max (0,1 - |{q_x} - {p_x}|) \cdot \max (0,1 - |{q_y} - {p_y}|)$ 是双线性插值核。

3.可变形卷积的应用

适应物体在不同图片中出现的复杂几何形变(如尺度、形态、非刚性形变等)，一直是物体识别领域的难点，可变形卷积网络给出了一个可行的解决方案。它可以端到端地学习几何形变的偏移量，不需要额外的监督信息，并且只增加了少许计算量，最终却能带来效果的显著提升。图1.10是可变形卷积的一组效果示意图，图中绿点是激活点，红点是激活点对应的三层3×3可变形卷积核的采样位置(共9×9×9=729个点)。可以看到，红色采样点基本覆盖了检测物体的全部区域，这说明可变形卷积会根据物体的尺度、形态进行自适应调整
在这里插入图片描述