作为一名软件工程师,大部分的工作时间都是在解决各种问题中度过的,相信大部分的工程师都有类似的感受。这些问题发生在不同的技术领域,不同的技术方向,不同的模块,甚至不同的环境下,不一而足,就像数学中的自然数可数无穷一样,我们可以一个个遍历它,但是无法穷尽所有的问题。这多少有点悲观,难道我们就没有办法了么? 不是这样的,问题有无数种,但是解决问题的通用思考方法却是有的,我们从一个数学概念讲起。
必要条件和充分条件
再进一步讨论之前,先来复习一下什么是必要条件和充分条件,这个概念应该是初中数学讲述的,并不陌生,但是真正能够掌握其确切定义的人却很少,如果用机械的方式加以定义,就是:
“当命题 ‘若p则q’ 为真,则p为充分条件,q为必要条件"
如果不结合具体的示例,可能很少有人会理解这句话,我们再分析的详细一点:
必要条件:对某事件的成立来说(至少)必要的条件。
充分条件:对某事件的成立来说(足够)充分的条件。
用这样得到方式解释好像还是不够清楚,举个例子:
居住在广东是居住在珠海的必要条件,居住在珠海市是居住在广东省的充分条件。
一个人如果居住在广东省,就有可能居住在珠海,而一个人如果居住在珠海,就一定居住在广东。根据这样的定义,如果我们把充分条件和必要条件联想成:
必要条件=宽松的条件
充分条件=严格的条件
或许会比较容易理解了。

类似的例子可以举很多,比如,考察一场考试年级第一和班级第一的关系。
如果同学A考了班级第一,那么他不一定是全级第一,但是如果这位同学考的是全年纪第一,那么它一定是班级第一,用图形表示就是:
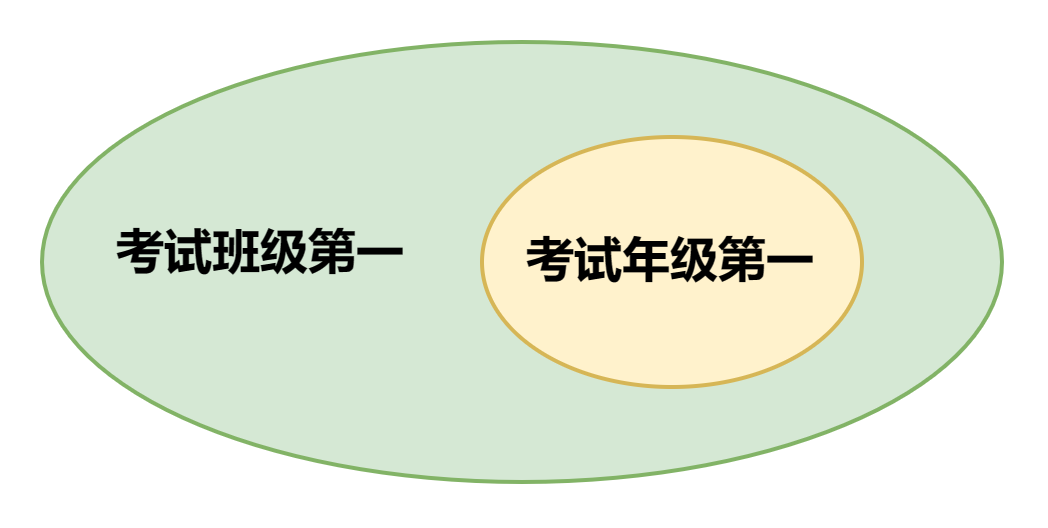
绿色部分就是那些班级考试第一,但是并不是全年级第一的同学,班级第一每个班都有一个,但是全年级第一只有一个。
根据上面两个例子,我们可以把必要条件和充分条件分别视为:
必要条件=大范围,充分条件=小范围
将上述内容整理后,就会是:
必要条件=宽松的条件 = 大范围
充分条件= 严格的条件=小范围
当逐渐缩小必要条件的范围,缩小到和充分条件重合的时候,我们就认为,我们找到了充要条件。

如何解BUG
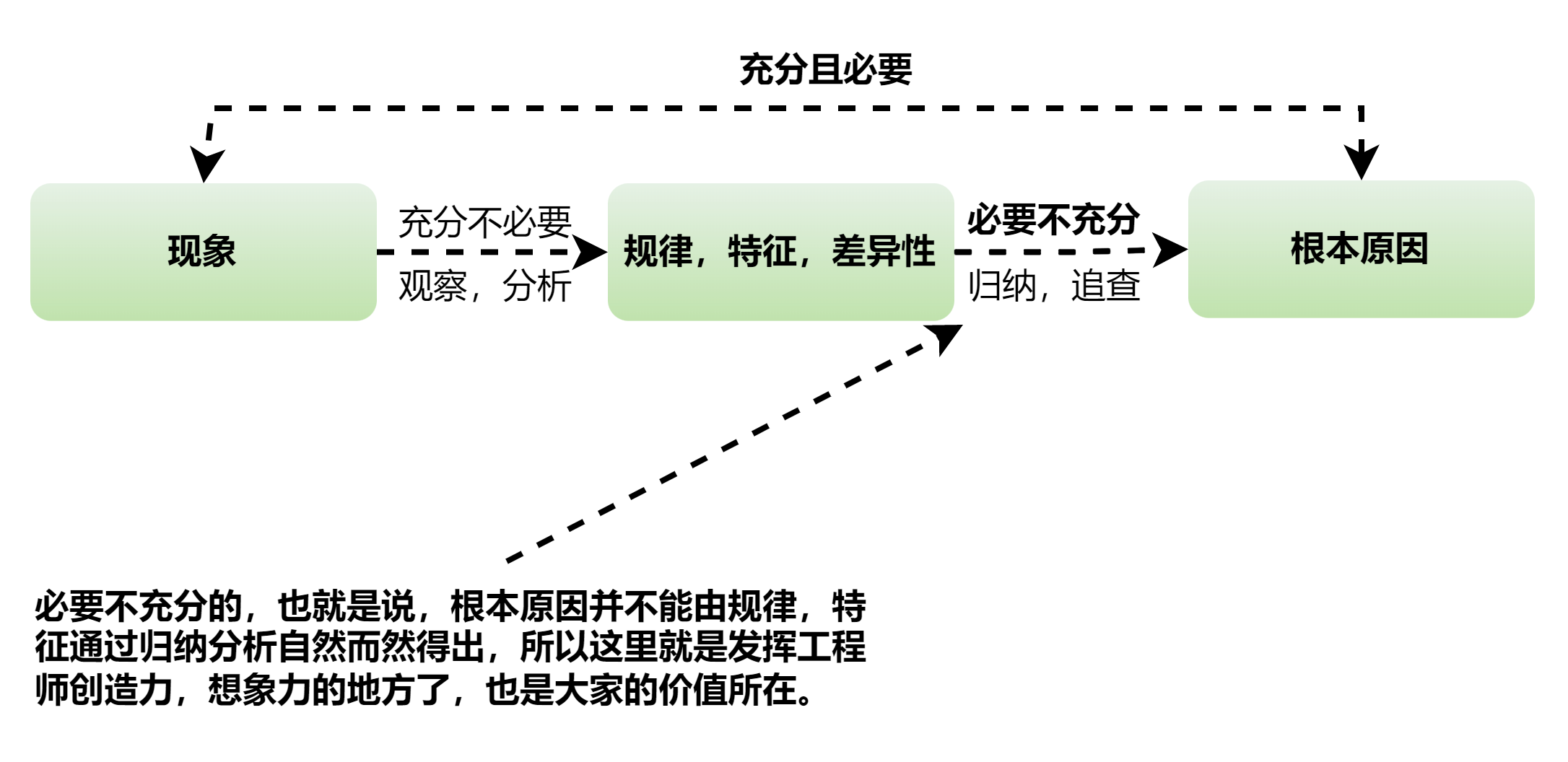
解BUG一般是根据现象找原因,我们要根据必要条件去寻找充分条件。

但是,通常一个问题可能会有多种现象,有些现象是观察到的,有些现象是待发现的。

这个时候,如果我们一味的从现象入手,拘泥于某个个别现象去寻找问题,很可能会陷入死胡同无法自拔,更何况现象空间是未知的,可能随时会有新的现象或者规律被发现,当这些现象和规律全部摆到你的面前的时候,处理的复杂性大大增加。
这个时候,我们总的方向是从各种现象入手,寻找这些现象背后的规律和联系,从中寻找最大公约,并且逐渐缩小这个公约范围直到它既能覆盖所有的现象,也能从逻辑上演绎出最后的问题。
所以,一开始从现象归纳到最大公约量的时候,我们用的是归纳的方式,这其中甚至会包含一些大胆的假设和猜测,但是我们基本定位到这个最大公约的范围之后,就可以大胆的使用演绎推理了,直到你发现,你演绎结果恰好是这个问题本身,这个时候,我们就找到了这个问题的rootcause.
如何打补丁
在芯片领域有一个流行的观点,如果硬件部署后出了BUG,那么问题也就成了feature.,一般需要用软件打补丁的方式去解决。一个好的补丁,一定是满足充分必要条件的补丁。