比赛链接 :
codeforces.com/contest/1941
A . Rudolf and the Ticket

直接暴力即可 ;
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
#define lowbit(x) (x&(-x))
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define int long long
typedef long long LL;
const int mod = 1e9+7;
const int N = 2000;
using namespace std;
int a[N] ,b[N] ;
inline void solve(){
int n , m , k ; cin >> n >> m >> k ;
for(int i=1;i<=n;i++) cin >> a[i] ;
for(int i=1;i<=m;i++) cin >> b[i] ;
int ans = 0 ;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(a[i] + b[j] <= k){
ans ++ ;
}
}
}
cout << ans << endl ;
}
signed main()
{
IOS
int _ = 1;
cin >> _;
while(_ --) solve();
return 0;
}B. Rudolf and 121

用贪心的思路 , 这个肯定是要从前往后来遍历的 ;
从左到右遍历一遍,最后看数组是不是全为0即可 ;
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
#define lowbit(x) (x&(-x))
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define int long long
typedef long long LL;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
using namespace std;
int a[N] ;
inline void solve() {
int n ; cin >> n ;
for(int i=1;i<=n;i++) {
cin >> a[i] ;
}
bool tag = true ;
for(int i=2;i<=n-1;i++){
int x = a[i-1] ;
a[i-1] -= x ;
a[i] -= 2 * x ;
a[i+1] -= x ;
if(a[i]<0 || a[i+1]<0){
tag = false ;
break ;
}
}
for(int i=1;i<=n;i++){
if(a[i]!=0){
tag = false ;
break ;
}
}
if(tag) cout << "YES" << endl ;
else cout << "NO" << endl ;
}
signed main()
{
IOS
int _ = 1;
cin >> _;
while (_--) solve();
return 0;
}C. Rudolf and the Ugly String

因为"map" 和 pie其实是互不相关的, 那么我们可以找到一个map就删掉a,找到一个pie的话,就删掉一个i,这样从前往后遍历即可 ,就是最优答案 ;
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
typedef long long LL;
const int mod = 1e9+7;
const int N = 2e5+10;
using namespace std;
string a = "pie" , b = "map" ;
inline void solve(){
int n ; cin >> n ;
string s ; cin >> s ;
s = ' ' + s ;
vector<int> idx ;
bool tag = true ;
for(int i=1;i<=n-2;i++){
if(s.substr(i,3) == a || s.substr(i,3) == b){
idx.push_back(i) ;
i += 2 ;
}
}
if(idx.size() == 0){
cout << 0 << endl ;
return ;
}else{
cout << (int)(idx.size()) << endl ;
}
}
signed main()
{
IOS
int _ = 1;
cin >> _;
while(_ --) solve();
return 0;
}D. Rudolf and the Ball Game
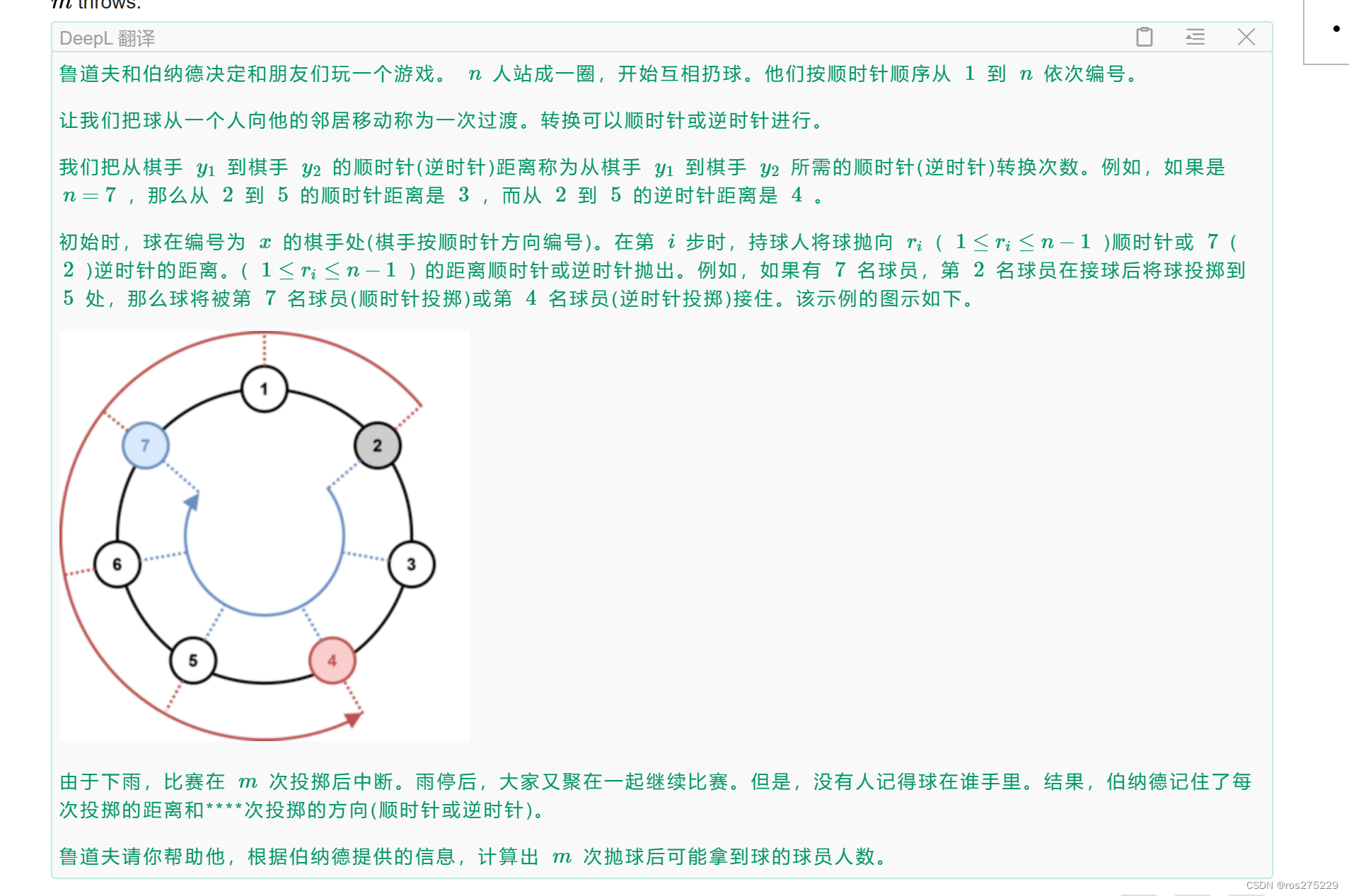
其实这题最重要的条件是 n * m <= 2e5:

那我们可以放心大胆的写二重循环来解决 ;
用一个bool数组dp记录当前的状态,dp[i]为true表示(i+1)人手里有球,为false表示无球,下一次的变化,用 一个bool数组g表示,遍历(0,n)对每一个dp[i] = true 的进行处理,也就是c[i]==0,1,?的三种情况分别处理即可 ;
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
typedef long long LL;
const int mod = 1e9+7;
const int N = 1e3+10;
using namespace std;
inline void solve(){
int n , m , x ; cin >> n >> m >> x ;
vector<int> dp(n) ;
x --; // 处理下标
dp[x] = 1;
for(int i=0;i<m;i++){
int r ; char c ;
cin >> r >> c ;
vector<int> g(n) ;// 代替dp数组的数组
for(int k=0;k<n;k++){
if(dp[k]){
if(c!='1') g[(k+r)%n] = 1 ;
if(c!='0') g[(k-r+n)%n] = 1 ;
}
}
dp = g ;
}
int ans = count(dp.begin(),dp.end(),1) ;
cout << ans << endl ;
for(int i=0;i<n;i++){
if(dp[i]){
cout << i + 1 << " " ;
}
}
cout << endl ;
}
signed main()
{
IOS
int _ = 1;
cin >> _;
while(_ --) solve();
return 0;
}