1. 冒泡排序
算法步骤:
- 比较相邻元素,如果第一个大于第二个则交换
- 从左往右遍历一遍,重复第一步,可以保证最大的元素在最后面
- 重复上述操作,可以得到第二大、第三大、…


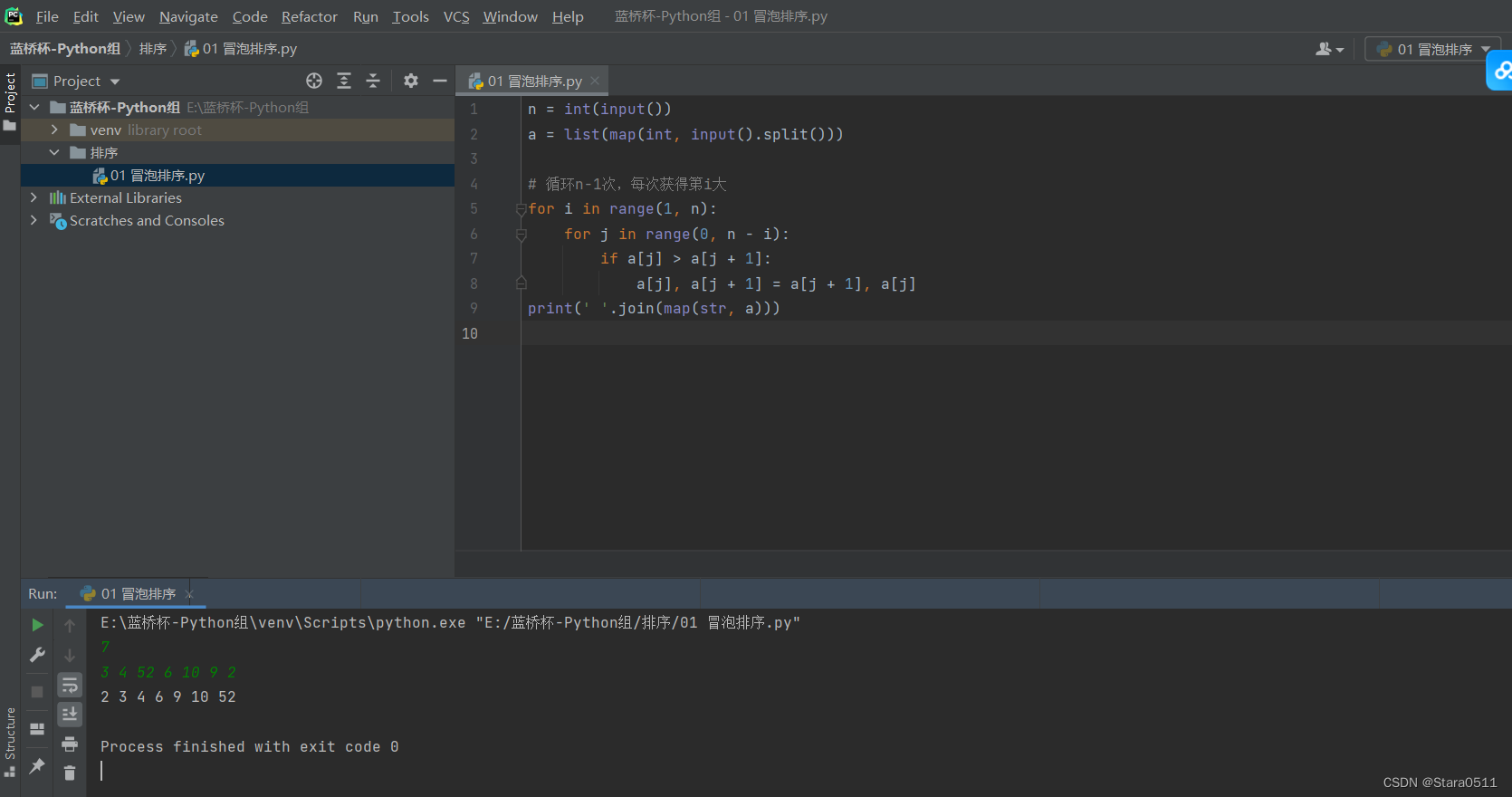
n = int(input())
a = list(map(int, input().split()))
# 循环n-1次,每次获得第i大
for i in range(1, n):
for j in range(0, n - i):
if a[j] > a[j + 1]:
a[j], a[j + 1] = a[j + 1], a[j]
print(' '.join(map(str, a)))
2. 选择排序
算法步骤:
- 从左往右找到最小元素,放在起始位置
- 重复上述步骤,依次找到第2小、第3小元素…

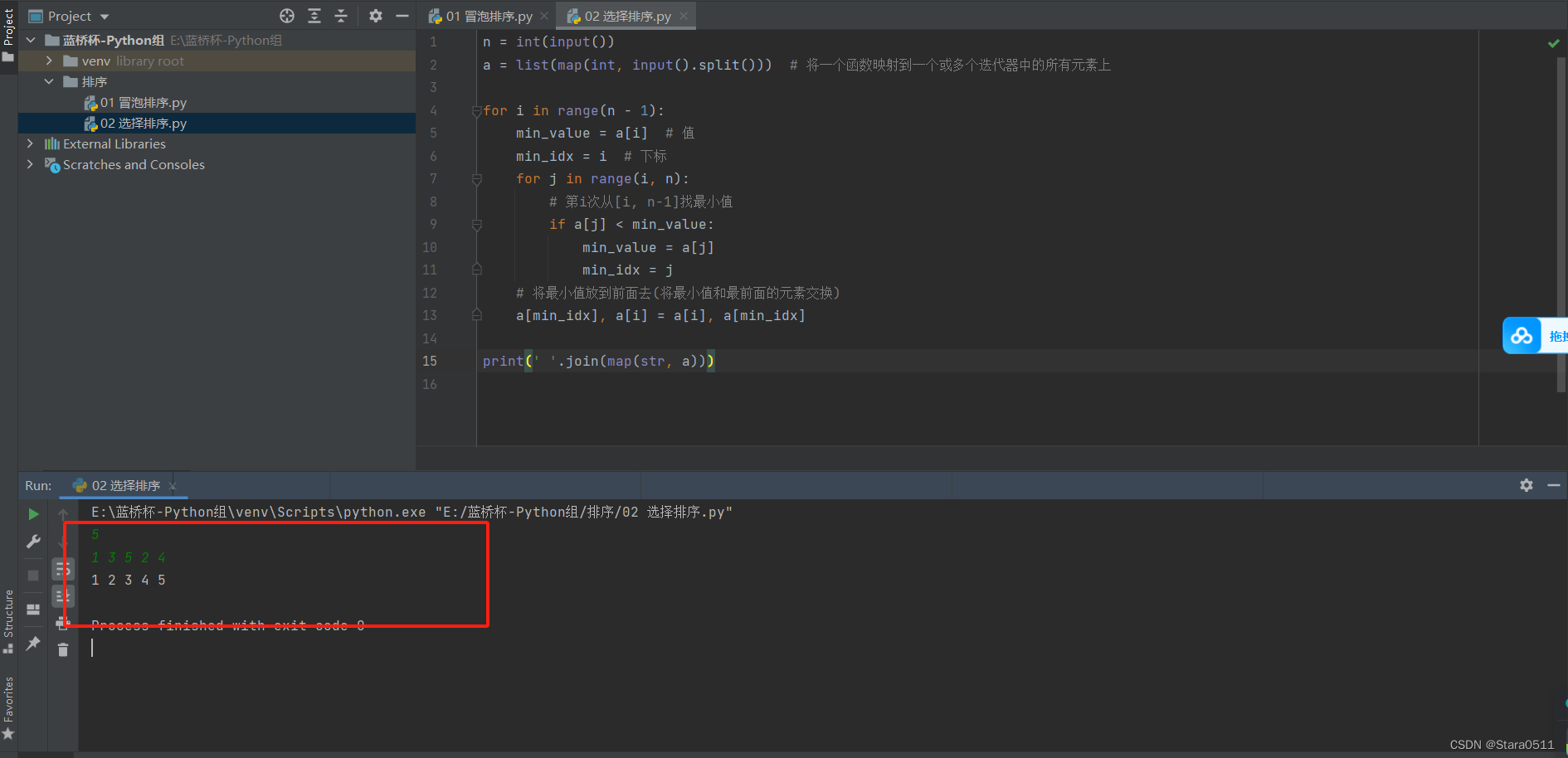
n = int(input())
a = list(map(int, input().split())) # 将一个函数映射到一个或多个迭代器中的所有元素上
for i in range(n - 1):
min_value = a[i] # 值
min_idx = i # 下标
for j in range(i, n):
# 第i次从[i, n-1]找最小值
if a[j] < min_value:
min_value = a[j]
min_idx = j
# 将最小值放到前面去(将最小值和最前面的元素交换)
a[min_idx], a[i] = a[i], a[min_idx]
print(' '.join(map(str, a)))
3. 插入排序
算法步骤:
- 第一个元素看做已排序,从左往右遍历每一个元素;
- 在已排序元素中从后往前扫描:如果当前元素大于新元素,则该元素移动到后一位
- 重复第二步直至找到小于等于新元素则停止

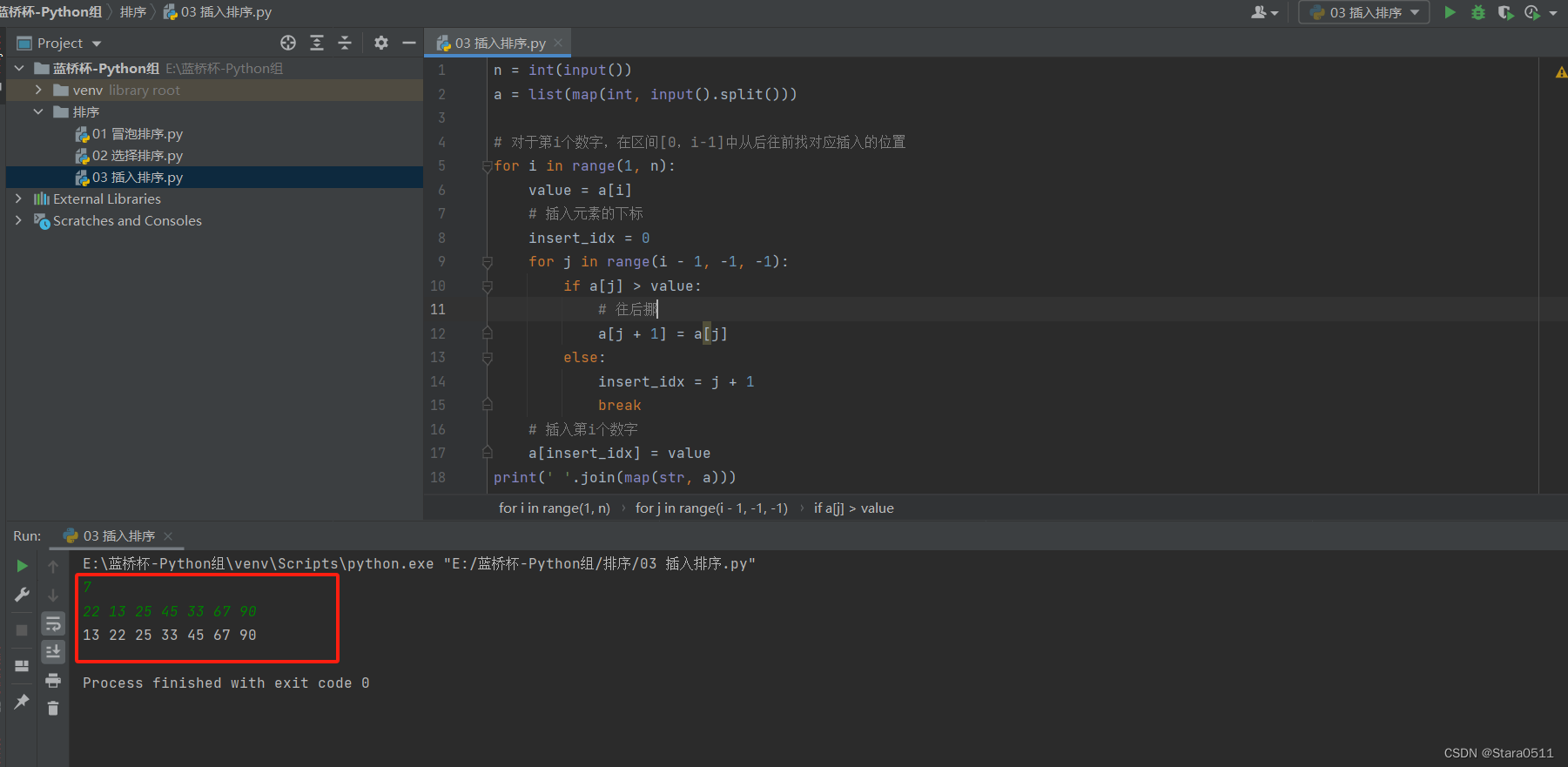
n = int(input())
a = list(map(int, input().split()))
# 对于第i个数字,在区间[0,i-1]中从后往前找对应插入的位置
for i in range(1, n):
value = a[i]
# 插入元素的下标
insert_idx = 0
for j in range(i - 1, -1, -1):
if a[j] > value:
# 往后挪
a[j + 1] = a[j]
else:
insert_idx = j + 1
break
# 插入第i个数字
a[insert_idx] = value
print(' '.join(map(str, a)))
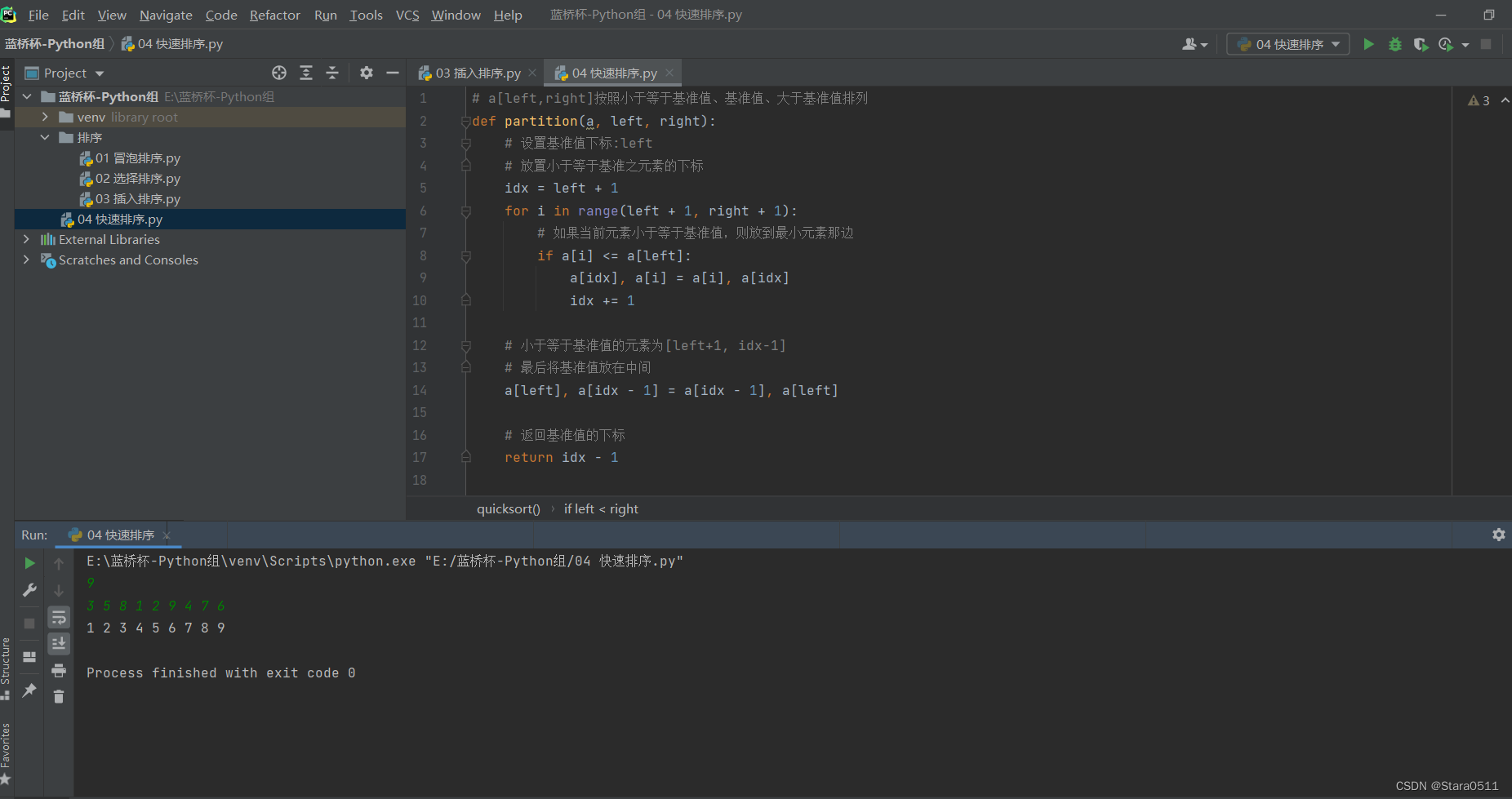
4. 快速排序
算法步骤:
- 找一个基准值X
- 把列分成三部分:小于等于X的数字,X, 大于X的数字
- 左半部分和右半部分递归使用该策略
例如:a=[3,5,8,1,2,9,4,7,6]
找到基准值3,[1,2] , 3, [5,8,9,4,7,6]
左半部分[1,2]作为一个子问题求解
右半部分 [5,8,9,4,7,6]作为一个子问题求解
# a[left,right]按照小于等于基准值、基准值、大于基准值排列
def partition(a, left, right):
# 设置基准值下标:left
# 放置小于等于基准之元素的下标
idx = left + 1
for i in range(left + 1, right + 1):
# 如果当前元素小于等于基准值,则放到最小元素那边
if a[i] <= a[left]:
a[idx], a[i] = a[i], a[idx]
idx += 1
# 小于等于基准值的元素为[left+1, idx-1]
# 最后将基准值放在中间
a[left], a[idx - 1] = a[idx - 1], a[left]
# 返回基准值的下标
return idx - 1
def quicksort(a, left, right):
if left < right:
mid = partition(a, left, right)
quicksort(a, left, mid - 1)
quicksort(a, mid + 1, right)
n = int(input())
a = list(map(int, input().split()))
quicksort(a, 0, n-1)
print(' '.join(map(str, a)))