概率是数据分析、机器学习中最基础的知识。也是在生活中最实用的一门学科,学了很多大道理不一定能过好一生,学好概率则有一定概率会变得更好。为大概率坚持,为小概率备份。
概率与分布
要想了解概率,首先得搞清楚概率和概率分布的问题
1.概率是什么?
定义:概率反映的是一个事件发生可能性的大小。概率将“可能性”量化了。
2.概率分布是什么?
定义:用于表述随机变量取值的概率规律。简而言之就是随机变量分布的规律。
3.概率与分布有什么关系?
概率和分布之间存在密切关系。概率是分布的具体取值,而分布是对随机变量在不同取值上的概率进行建模。这两者相辅相成,共同构建了对不确定性的数学描述。
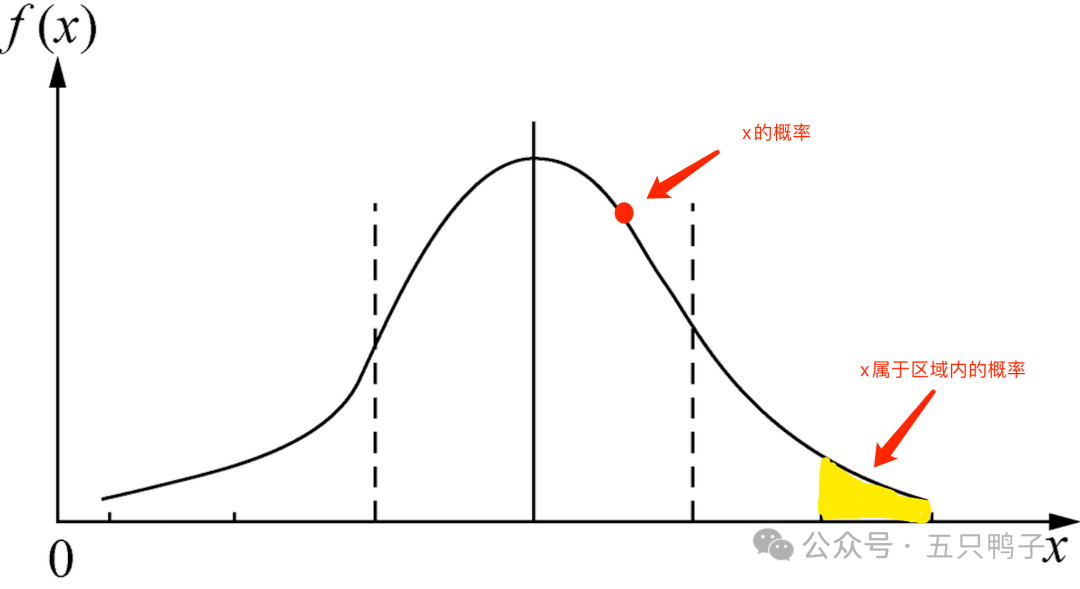
例如:下图是一个正态分布,红点是表示在这个分布中,为x的概率,黄色的区域表示在这个分布中x属于这个黄色区域内的概率
常见的概率分布
在搞清楚概率分布之前我们还得先了解随机变量
什么是随机变量?
定义:表示随机试验各种结果的实值单值函数。是不是很晕,比文言文还难懂,其实简单的理解:随着随机试验的结果变化而变化的变量,叫做随机变量
比如抛骰子实验,观察点数,设抛出的点数结果为X,则X有6种可能的结果,而且每次出现的点数,都是随机性的,那么这样的变量叫做随机变量。
随机变量分为离散型随机变量与非离散型随机变量两种。
离散型:变量的取值个数是有限的,可数的。
例如抛硬币,有正反两种可能;抛骰子有6中可能等,都是可数的。
非离散型:变量的取值个数无限,取值范围为全体实数。非离散型中可以分为连续性(绝大部分)和混合型
例如:长度、速度、重量、体积、温度、力量等。这些都有无限个值,无法列举。
发现没有,这些变量都是一种度量
离散概率分布
伯努利分布(Bernoulli Distribution)
伯努利分布是描述只有两个可能结果的随机试验,如硬币的正反面。
如果投一枚硬币,正面为1,反面为0。概率质量函数为 P(x=1) =p, P(x=0)=1-p
二项分布(Binomial Distribution)
描述多次独立伯努利试验的概率。也就是说在n次试验中正好得到k次成功的概率。
如果逆向看伯努利分布就是n=1的二项分布。
那么实验了n次,有k次成功,就意味着有n-k次失败。
成功的概率为p,失败的概率为1-p
注意这里是不管实验结果的顺序的,不论是第几次成功或失败都没影响,只管最终成功和失败的次数,就很自然的使用了排列组合里面的组合C。
二项分布的概率公式则描述为
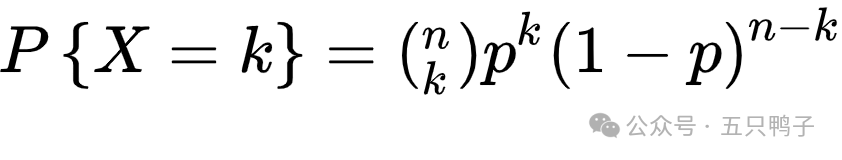
多项分布(Multinomial Distribution)
是二项分布的推广,二项分布描述的是实验结果只有两种的分布。多项分布则是描述实验结果有多种可能的分布。例如骰子的6种可能。
某随机实验如果有k个可能结果A1、A2、…、Ak,分别将他们的出现次数记为随机变量X1、X2、…、Xk,它们的概率分布分别是p1,p2,…,pk,那么在n次采样的总结果中,A1出现n1次、A2出现n2次、…、Ak出现nk次的这种事件的出现概率P有下面公式:
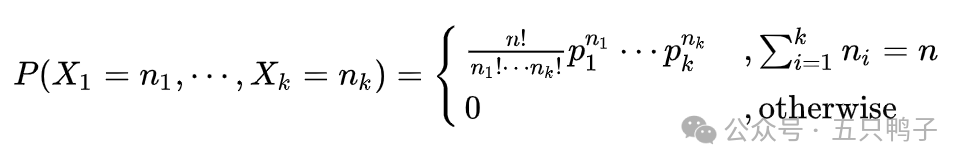
连续概率分布
正态分布(Normal Distribution)
又称为高斯分布(Gaussian distribution),是统计学中最常见的一种分布,正态分布曲线两头低,中间高,左右对称,因图形像大钟,因此又称为钟形曲线。
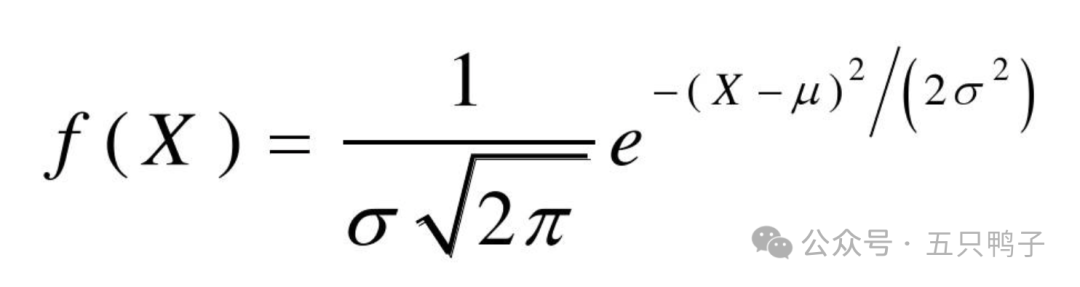
正态分布的密度函数
式中μ为均值;σ是标准差;π为圆周率≈3.1415926;e为自然常数≈2.71828
这个公式中主要关注均值 μ 和标准差 σ,均值 μ 决定分布度的偏度
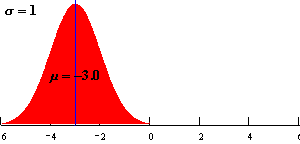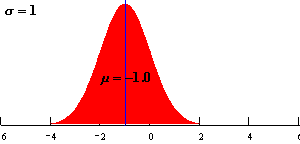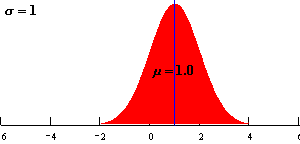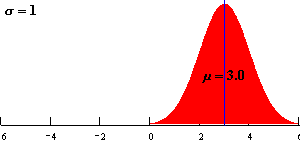
均值 μ决定了曲线横轴的位置,μ增大曲线向横轴右移;μ减小曲线向横轴左移。
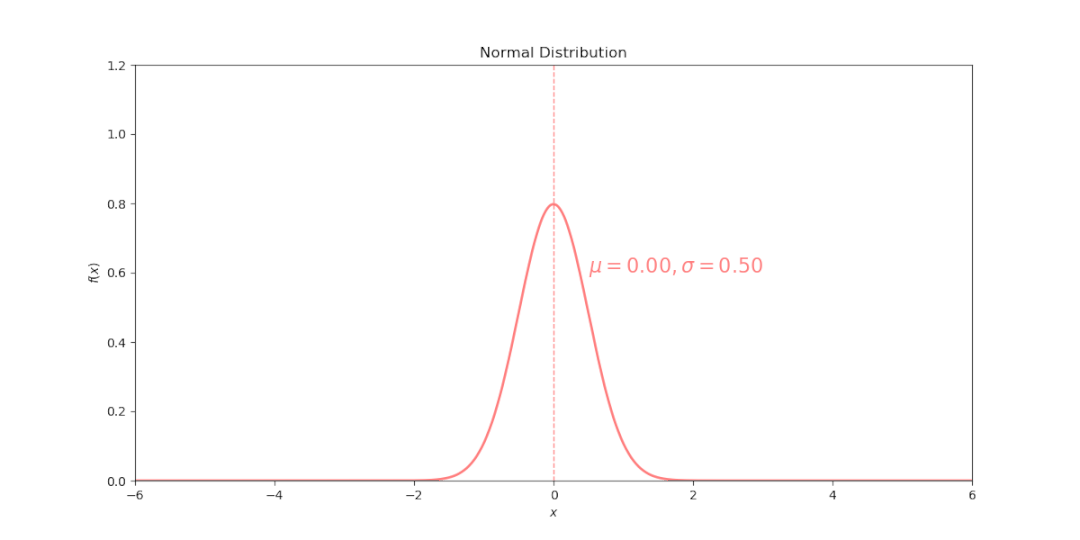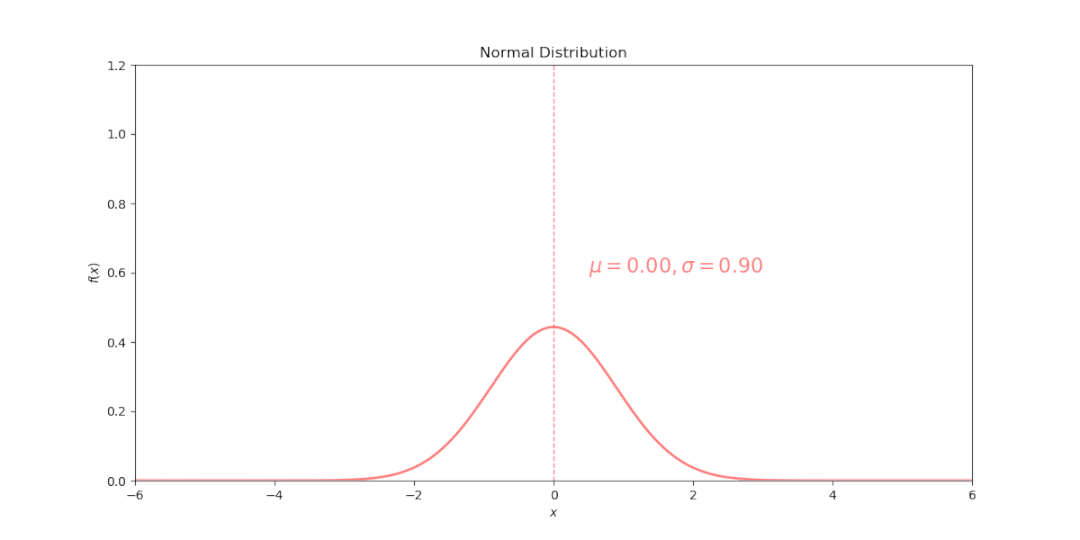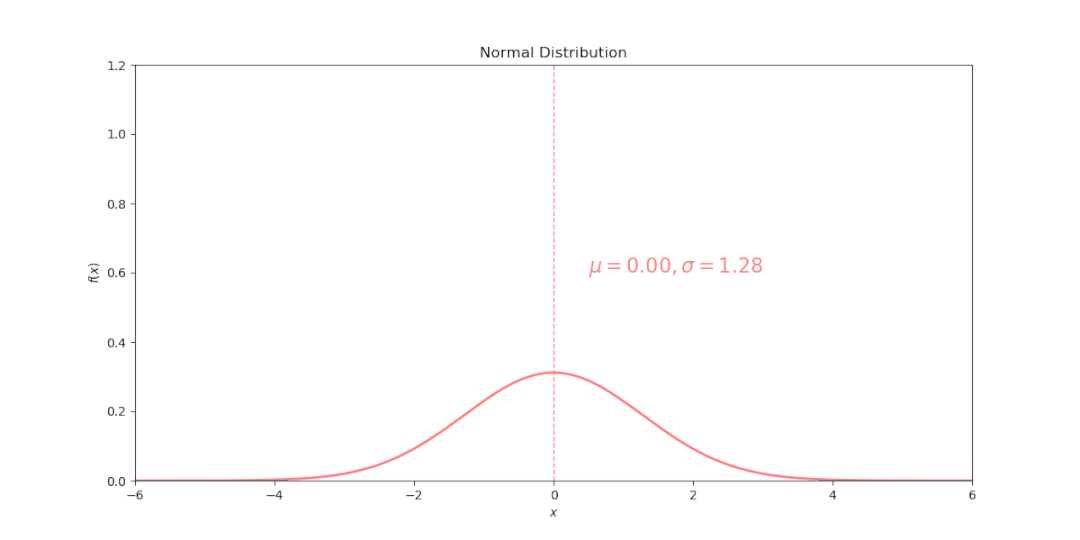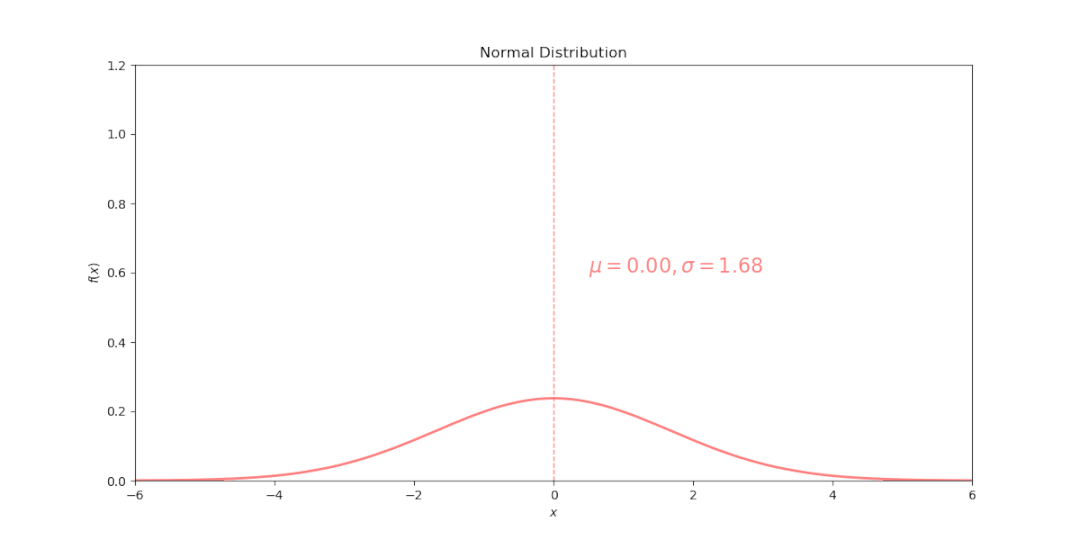
标准差σ决定曲线的宽度和高度,σ越大,曲线越宽越平坦(矮胖),表明数据越分散,反之亦然。
指数分布(Exponential Distribution)
用于描述独立随机时间发生的时间间隔或间隔事件的概率分布,在可靠性分析和排队论中比较常见,其中在排队论中指数分布常用于描述服务时间。例如等待公交车进站的时间间隔。
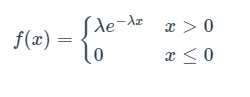
指数分布密度函数
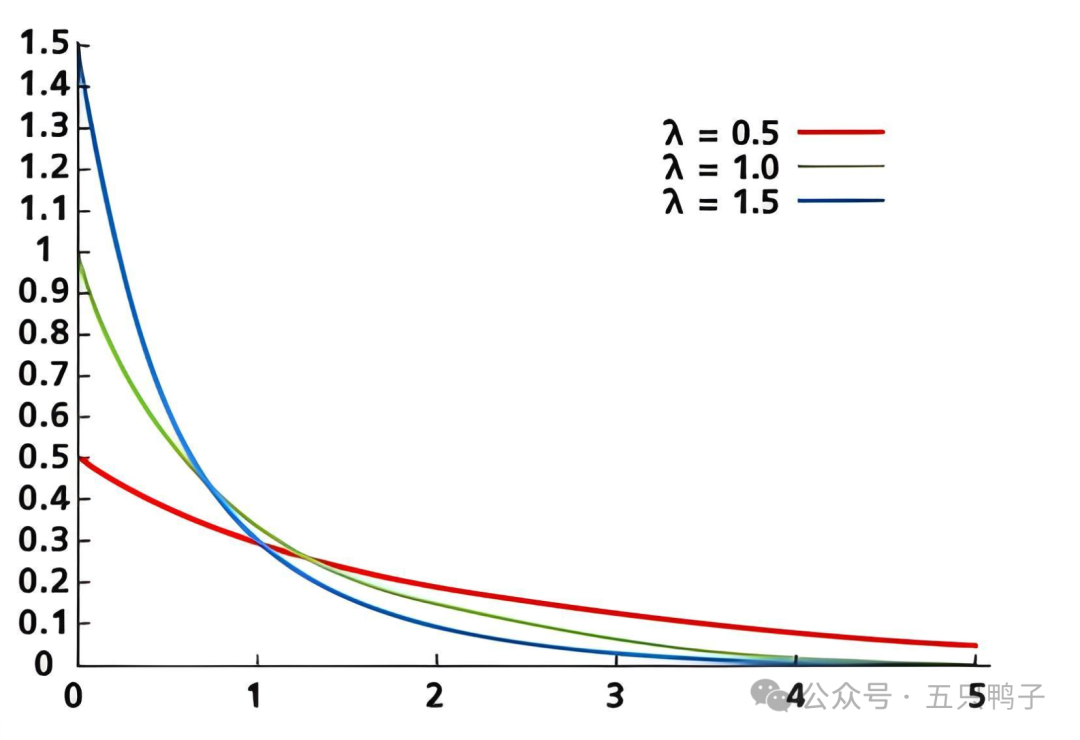
指数分布图
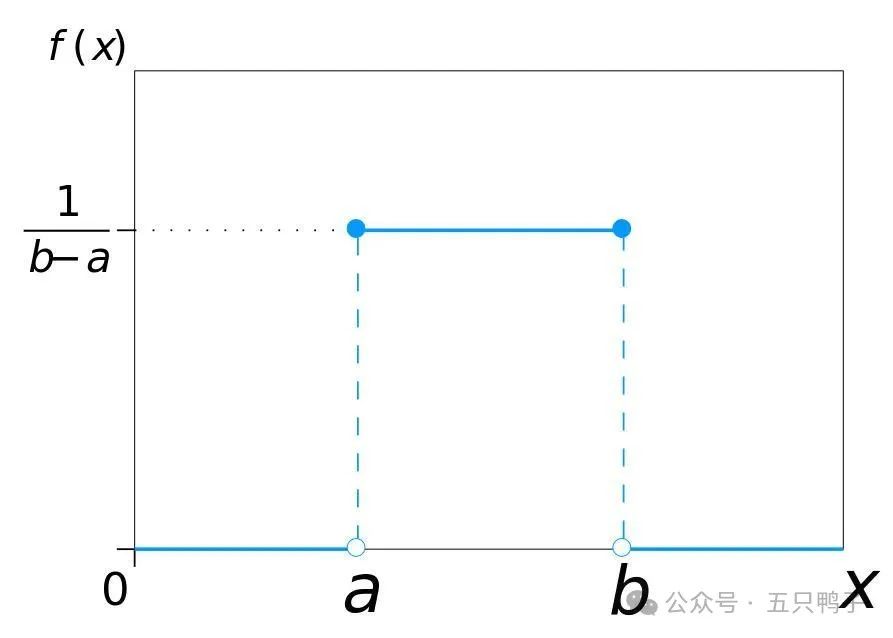
均匀分布(Uniform Distribution)
均匀分布在区间内所有取值的概率都相等,因为图形是一个矩形,所以也叫矩形分布,均匀分布由两个参数a和b定义,它们是数轴上的最小值和最大值。密度函数非常简单 f(x) = 1/ (b-a)
泊松分布(Poisson distribution)
主要用于估计在特定时间段或空间中某事件发生的次数,例如一小时内到达店里的人数。满足以下两个性质,则水机变量服从泊松分布
-
在任意两个相等长度的区间上,事件发生的概率相等。
-
事件在某一区间上是否发生与事件在其他区间上是否发生是相互独立的。
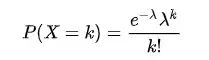
k表示事件在一个区间发生k次的概率;λ表示事件在一个区间发生次数的数学期望或均值;其中λ越大越接近于正态分布,当λ=50时,可以认为泊松分布呈现正态分布了。
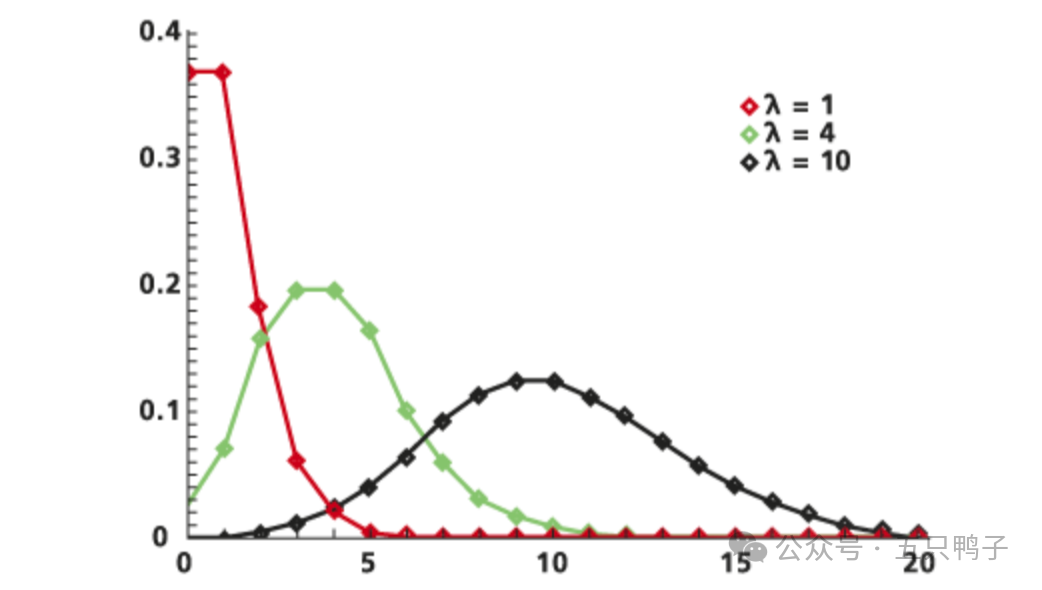
而且泊松分布是由二项分布推导而来,当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。通常当n≧20,p≦0.05时,二项分布就可以用泊松公式近似的计算。
除此之外还有一些正态分布相关的分布
例如:
卡方分布(Chi-Square Distribution)用于描述多个相互独立标准正态分布的随机变量的平方和,有几个数就是服从自由度为几的卡方分布,自由度越大,越接近于正态分布。