一.topk问题
取N个数中最大(小)的前k个值,N远大于k
这道题可以用堆的方法来解决,首先取这N个数的前k个值,用它们建堆
时间复杂度O(k)

之后将剩余的N-k个数据依次与堆顶数据进行比较,如果比堆顶数据大,则将堆顶数据覆盖后向下调整
时间复杂度(N-k)*log(N)
总共的时间复杂度为O(N*log(N))
void adjustDown(HeapDataType* p, int size, int parent)
{
int child = parent * 2 + 1;
if (p[child] > p[child + 1])
child++;
while (child <= size)
{
if (child + 1 <= size && p[parent] > p[child])
{
Swap(&p[parent], &p[child]);
parent = child;
child = child * 2 + 1;
if (p[child] > p[child + 1])
child++;
}
else break;
}
}
void heapTopk(HeapDataType* p, int size)
{
int k;
scanf_s("%d", &k);
for (int i = (k - 1 - 1) / 2; i >= 0; i--)
adjustDown(p, k, i);
while (size - k > 0)
{
if (p[size - 1] > p[0])
p[0] = p[size - 1];
adjustDown(p, k, 0);
size--;
}
}二.链式二叉树
用数组建堆只能用在完全二叉树的情况下,那其他情况该怎么办?
显然顺序表已经行不通了,那我们不妨换链表试试
链式二叉树是一种用链表结构存储二叉树的方式,每个节点包含一个值以及左右子节点的指针。其遍历方式分为前序遍历、中序遍历和后序遍历。
1.前序遍历(根->左子树->右子树)

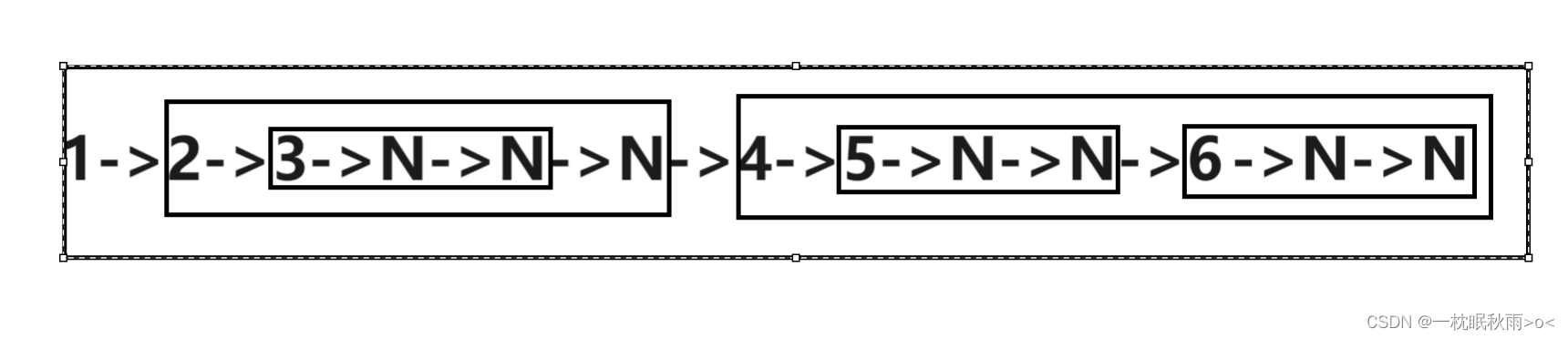
以这个图为例
首先访问根的数据,也就是1
然后访问1的左子树,也就是以2为根节点的树,然后再访问2的左子树,也就是以3为根节点的树,直到访问到空节点,
同理访问右子树
1->2->3->N->N->N->4->5->N->N->6->N->N
void preTreeNode(TNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
printf("%d ", root->data);
preTreeNode(root->left);
preTreeNode(root->right);
}2.中序遍历(左子树->根->右子树)

首先访问1的左子树,也就是以2为根节点的树,然后访问2的左子树,也就是以3为根节点的树,直到访问到空,最后回到根节点1,然后同理去访问右子树
N->3->N->2->N->1->N->5->N->4->N->6->N

void inTreeNode(TNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
inTreeNode(root->left);
printf("%d ", root->data);
inTreeNode(root->right);
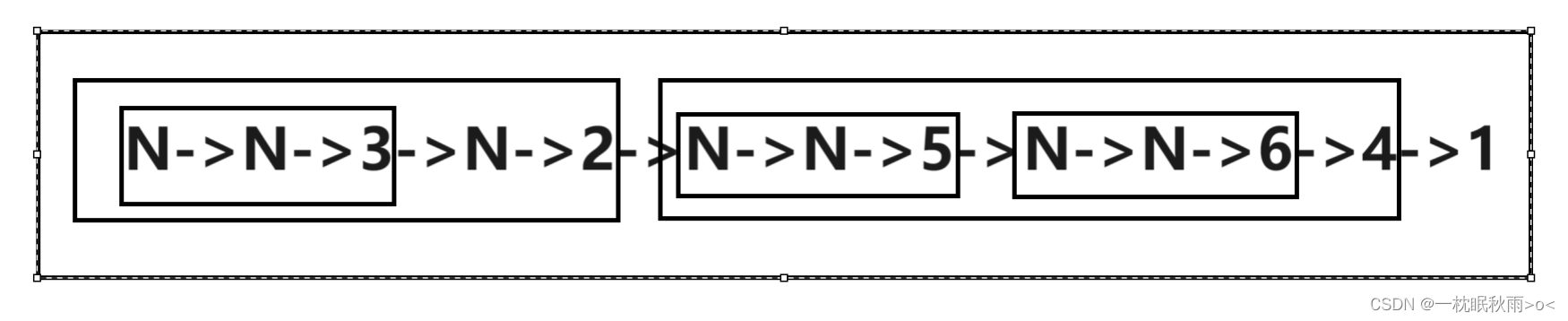
}3.后序遍历(左子树->右子树->根)
N->N->3->N->2->N->N->5->N->N->6->4->1
void postTreeNode(TNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
postTreeNode(root->left);
postTreeNode(root->right);
printf("%d ", root->data);
}三.双路递归
1.概念及应用场景
双路递归是一种算法思想,指的是在递归过程中同时处理两个子问题,从而提高递归的效率和性能。例如,在归并排序中,可以同时对左半部分和右半部分进行排序,然后将它们合并成一个有序的序列,从而实现排序的目的。
归并排序是一种基于分治思想的排序算法,其基本思想是将一个数组分成两半,对每一半进行排序,然后将排序后的两个半数组合并成一个有序的数组。归并排序可以用于内排序和外排序,其时间复杂度为 O(nlogn),是一种稳定的排序算法。在处理一些问题时,双路递归比单路递归更有效率,例如在归并排序中,双路递归可以同时对左半部分和右半部分进行排序,然后将它们合并成一个有序的序列,从而减少了排序的时间复杂度。
另外,在一些搜索问题中,双路递归也可以更快地找到目标元素,例如在二叉搜索树中,可以同时从左子树和右子树进行搜索,从而更快地找到目标元素。
总的来说,双路递归适用于那些可以将问题拆分成两个子问题,并且可以同时处理这两个子问题的情况。在这种情况下,双路递归可以减少递归的次数,提高算法的效率。但是,使用双路递归也需要注意一些问题,例如递归深度的增加和内存的消耗等。
2.与单路递归的区别
单路递归和双路递归都有各自的优缺点,下面是它们的一些特点:
- 单路递归的优点:
- - 代码简单易懂,容易理解和实现。
- - 适用于一些简单的问题,如斐波那契数列、阶乘等。
- 单路递归的缺点:
- - 可能会出现栈溢出的情况,尤其是在处理大数据量时。
- - 对于某些问题可能会出现重复计算,导致效率低下。
- 双路递归的优点:
- - 可以减少重复计算,提高效率。
- - 可以处理一些复杂的问题,如二叉树的遍历、图的深度优先搜索等。
- 双路递归的缺点:
- - 代码相对复杂,不易理解和维护。
- - 可能会消耗更多的内存,尤其是在处理大规模数据时。
需要根据具体情况选择使用单路递归还是双路递归。如果问题规模较小,单路递归可能更适合;如果问题规模较大或需要更高的效率,双路递归可能更合适。同时,还需要考虑程序的内存使用情况和算法的可扩展性等因素。
3.空间复用
空间复用是指在不同的时间段内,不同的用户共享相同的一组资源,这样可以降低成本,提高资源利用率。空间复用是多用户接入的重要技术,它可以实现数据、信号、频率、时间等方面的共享。
以LTE通信为例,空间复用是利用两个较大的天线阵元或赋形波束之间的不相关性,向一个终端/基站并行发射多个数据流,以实现链路容量的提高。双路递归中的空间复用是指在递归过程中重复利用之前开辟的空间,以减少内存使用量。以 longlong Fib(size_t N) 函数为例,该函数的作用是计算斐波那契数列中第 N 个数的值。在递归计算 Fib(2) 时,会开辟一块空间来存储计算结果;在计算 Fib(1) 时,会复用 Fib(2) 开辟的空间;在计算 Fib(5) 时,会复用 Fib(4) 开辟的空间,依此类推。通过这种方式,可以有效减少内存的使用,提高程序的运行效率。
如果你想了解更多关于双路递归的内容,请提供详细信息继续向我提问。