查找和最小的 K 对数字

news2024/11/25 4:41:24

优质博文IT-BLOG-CN

一、题目

给定两个以非递减顺序排列的整数数组nums1和nums2, 以及一个整数k。

定义一对值(u,v)，其中第一个元素来自nums1，第二个元素来自nums2。

请找到和最小的k个数对(u1,v1), (u2,v2) ... (uk,vk)。

示例 1:
输入: nums1 = [1,7,11], nums2 = [2,4,6], k = 3
输出: [1,2],[1,4],[1,6]
解释: 返回序列中的前3对数：[1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]

示例 2:
输入: nums1 = [1,1,2], nums2 = [1,2,3], k = 2
输出: [1,1],[1,1]
解释: 返回序列中的前2对数：[1,1],[1,1],[1,2],[2,1],[1,2],[2,2],[1,3],[1,3],[2,3]

1 <= nums1.length, nums2.length <= 105
-109 <= nums1[i], nums2[i] <= 109
nums1和nums2均为升序排列
1 <= k <= 104
k <= nums1.length * nums2.length

二、代码

优先队列

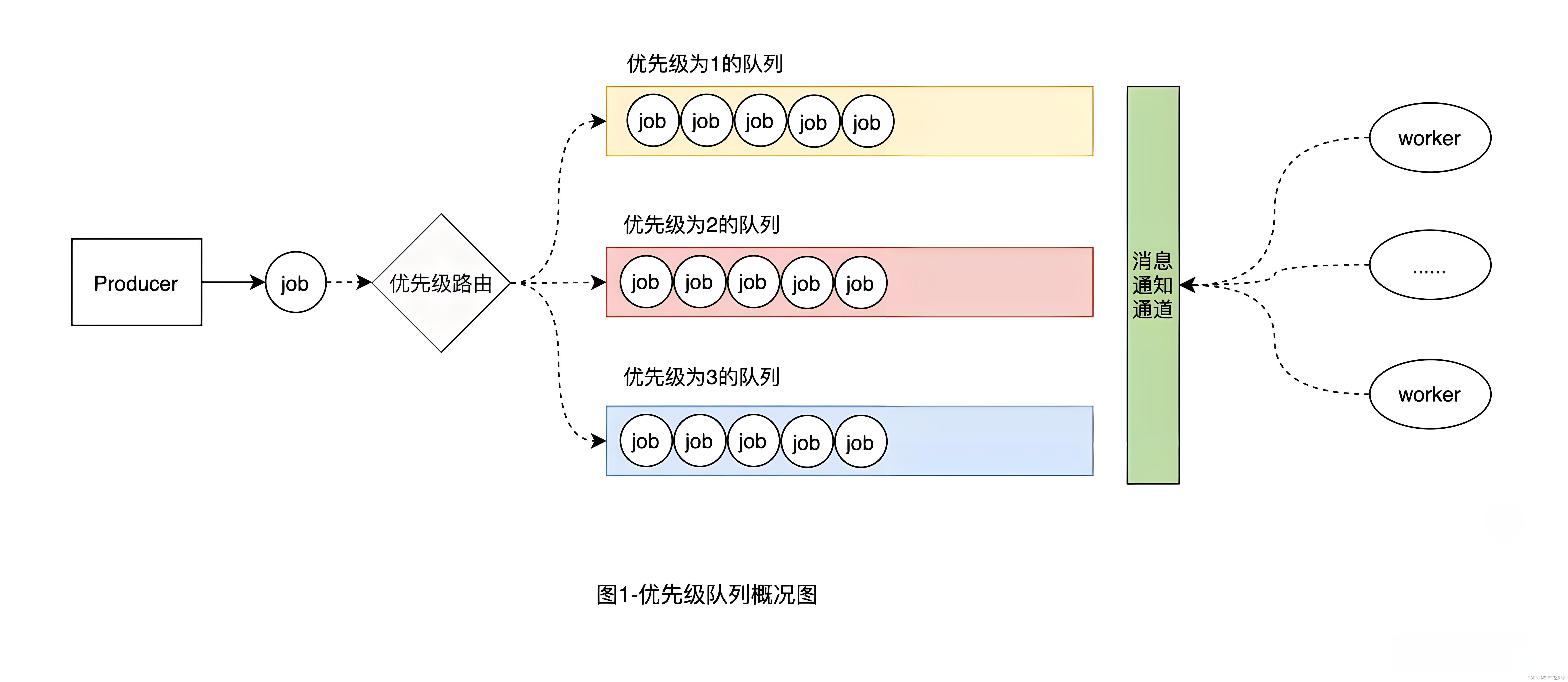
在这里插入图片描述

对于已经按升序排列的两个数组nums1,nums2，长度分别为length1,length2，我们可以知道和最小的数对一定为 (nums1[0],nums2[0])，和最大的数对一定为(nums1[length1−1],nums2[length2−1])。本题要求找到最小的k个数对，最直接的办法是可以将所有的数对求出来，然后利用排序或者TopK解法求出最小的k个数对即可。实际求解时可以不用求出所有的数对，只需从所有符合待选的数对中选出最小的即可，假设当前已选的前n小数对的索引分别为(a1,b1),(a2,b2),(a3,b3),…,(an,bn)，由于两个数组都是按照升序进行排序的，则可以推出第n+1小的数对的索引选择范围为(a1+1,b1),(a1,b1+1),(a2+1,b2),(a2,b2+1),(a3+1,b3),(a3,b3+1),…,(an+1,bn),(an,bn+1)，假设我们利用堆的特性可以求出待选范围中最小数对的索引为(ai,bi)，同时将新的待选的数对(ai+1,bi),(ai,bi+1)加入到堆中，直到我们选出 kkk 个数对即可。

如果我们每次都将已选的数对(ai,bi)的待选索引(ai+1,bi),(ai,bi+1)加入到堆中则可能出现重复的问题，一般需要设置标记位解决去重的问题。我们可以将nums1的前k个索引数对(0,0),(1,0),…,(k−1,0)加入到队列中，每次从队列中取出元素(x,y)时，我们只需要将nums2的索引增加即可，这样避免了重复加入元素的问题。

class Solution {
    public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
        PriorityQueue<int[]> pq = new PriorityQueue<>(k, (o1, o2)->{
            return nums1[o1[0]] + nums2[o1[1]] - nums1[o2[0]] - nums2[o2[1]];
        });
        List<List<Integer>> ans = new ArrayList<>();
        int m = nums1.length;
        int n = nums2.length;
        for (int i = 0; i < Math.min(m, k); i++) {
            pq.offer(new int[]{i,0});
        }
        while (k-- > 0 && !pq.isEmpty()) {
            int[] idxPair = pq.poll();
            List<Integer> list = new ArrayList<>();
            list.add(nums1[idxPair[0]]);
            list.add(nums2[idxPair[1]]);
            ans.add(list);
            if (idxPair[1] + 1 < n) {
                pq.offer(new int[]{idxPair[0], idxPair[1] + 1});
            }
        }
        
        return ans;
    }
}

时间复杂度： O(klog⁡k)，其中k是选择的数对的数目。优先队列中最多只保存k个元素，每次压入新的元素队列进行调整的时间复杂度为log⁡k，入队操作一共有2k次, 一共需要从队列中弹出k个数据。
空间复杂度： O(k)。优先队列中最多只保存k个元素。

二分查找

我们利用二分查找找到第k小的数对和为pairSum。利用滑动窗口即可计算出两个数组中满足数对和小于等于目标值target的数对有多少个，我们找到最小的target且满足小于等于它的数对数目刚好大于等于k即为目标值pairSum，然后在数组中找到最小的 kkk 个数对满足数对和小于等于pairSum。

由于题目中数组nums1,nums2中的元素存在重复，因此我们不能简单的利用滑动窗口找到所有满足小于等于pairSum的数对。因为存在小于等于pairSum的数对和的数目大于k，因此数对和等于pairSum的数对不一定就属于最小的k个数对。
首先利用滑动窗口找到所有小于pairSum的数对，假设数对和小于pairSum的数目为x个，然后再利用二分查找在数组中找到k−x个和等于pairSum的数对即可。

class Solution {
    public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
        int m = nums1.length;
        int n = nums2.length;

        /*二分查找第 k 小的数对和的大小*/
        int left = nums1[0] + nums2[0];
        int right = nums1[m - 1] + nums2[n - 1];
        int pairSum = right;
        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            long cnt = 0;
            int start = 0;
            int end = n - 1;
            while (start < m && end >= 0) {
                if (nums1[start] + nums2[end] > mid) {
                    end--;
                } else {
                    cnt += end + 1;
                    start++;
                }
            }
            if (cnt < k) {
                left = mid + 1;
            } else {
                pairSum = mid;
                right = mid - 1;
            }
        }

        List<List<Integer>> ans = new ArrayList<>();
        int pos = n - 1;
        /*找到小于目标值 pairSum 的数对*/
        for (int i = 0; i < m; i++) {
            while (pos >= 0 && nums1[i] + nums2[pos] >= pairSum) {
                pos--;
            }
            for (int j = 0; j <= pos && k > 0; j++, k--) {
                List<Integer> list = new ArrayList<>();
                list.add(nums1[i]);
                list.add(nums2[j]);
                ans.add(list);
            }
        }

        /*找到等于目标值 pairSum 的数对*/
        pos = n - 1;
        for (int i = 0; i < m && k > 0; i++) {
            int start1 = i;
            while (i < m - 1 && nums1[i] == nums1[i + 1]) {
                i++;
            }
            while (pos >= 0 && nums1[i] + nums2[pos] > pairSum) {
                pos--;
            }
            int start2 = pos;
            while (pos > 0 && nums2[pos] == nums2[pos - 1]) {
                pos--;
            }
            if (nums1[i] + nums2[pos] != pairSum) {
                continue;
            }
            int count = (int) Math.min(k, (long) (i - start1 + 1) * (start2 - pos + 1));
            for (int j = 0; j < count && k > 0; j++, k--) {
                List<Integer> list = new ArrayList<>();
                list.add(nums1[i]);
                list.add(nums2[pos]);
                ans.add(list);
            }
        }
        return ans;
    }
}

时间复杂度： O(k+(m+n)×log⁡(diff(nums1)+diff(nums2)))，其中m,n表示数组nums1,nums2的长度，diff(arr)\textit{diff}(arr)diff(arr) 表示数组arr中最大元素与最小元素之差，diff(nums1)=max⁡(nums1)−min⁡(nums1),diff(nums2)=max⁡(nums2)−min⁡(nums2))。我们利用二分查找找到满足要求的数对和的时间复杂度为(m+n)×log⁡(diff(nums1)+diff(nums2))，我们利用滑动窗口找到小于等于目标值的k个数对的时间复杂度为O(2×(k+m+n))，所以总的时间复杂度O(2×(k+m+n)+(m+n)×log⁡(diff(nums1)+diff(nums2)))=k+(m+n)×log⁡(diff(nums1)+diff(nums2))。
空间复杂度： O(1)，除了函数返回值以外，不需要额外的存储空间。