文章目录
- 把普通数组转换大顶堆数组
- 堆增删改查替换
- 堆排序
把普通数组转换大顶堆数组
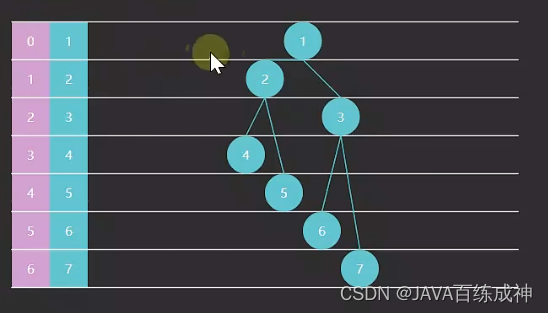
该方式适用索引为0起点的堆
在堆(Heap)这种数据结构中,节点被分为两类:叶子节点(Leaf Nodes)和非叶子节点(Non-Leaf Nodes)。
叶子节点是指没有子节点的节点,它们位于堆的最底层。在堆中,叶子节点的数量总是大于或等于非叶子节点的数量。
非叶子节点是指至少有一个子节点的节点,它们位于堆的上层。在二叉堆(Binary Heap)中,非叶子节点的数量总是等于总节点数的一半(向上取整)。
在堆的操作中,非叶子节点的重要性体现在维护堆的性质(如最大堆或最小堆)方面。当插入或删除节点时,可能需要对非叶子节点进行调整,以确保堆的性质得到维护。
package Heap;
import java.util.Arrays;
//大顶堆
public class MaxHeap {
int [] array;
int size;
public MaxHeap(int capacity){
this.array=new int[capacity];
}
public MaxHeap(int [] array){
this.array=array;
this.size=array.length;
heapify();
}
//建堆
private void heapify(){
// size/2-1找到非叶子节点
for (int i=size/2-1;i>=0;i--){
down(i);
}
}
//将 parent 索引处的元素下潜:与两个孩子较大者交换,直至没孩子
//或者孩子没他大
private void down(int parent){
int left = parent*2+1;
int right=left+1;
int max = parent;
if (left<size && array[left]> array[max]){
max=left;
}
if (left<size && array[right]> array[max]){
max=right;
}
if (max!=parent){//找到了更大的孩子
swap(max,parent);
down(max);
}
}
//交换两个索引
private void swap(int i,int j){
int t = array[i];
array[i]=array[j];
array[j]=t;
}
public static void main(String[] args) {
int [] arr= {1,2,3,4,5,6,7};
MaxHeap maxHeap = new MaxHeap(arr);
System.out.println(Arrays.toString(maxHeap.array));
}
}
堆增删改查替换
package Heap;
import java.util.Arrays;
// 大顶堆
public class MaxHeap {
int[] array;
int size;
public MaxHeap(int capacity) {
this.array = new int[capacity];
}
public MaxHeap(int[] array) {
this.array = array;
this.size = array.length;
heapify();
}
// 获取堆顶元素
public int peek() {
return array[0];
}
// 删除堆顶元素
public int poll() {
int top = array[0];
swap(0, size - 1);
size--;
down(0);
return top;
}
// 删除指定索引
public int poll(int index) {
int delete = array[index];
swap(index, size - 1);
size--;
// 维护堆的性质
if (index > 0 && array[index] > array[(index - 1) / 2]) {
up(index);
} else {
down(index);
}
return delete;
}
// 替换指定索引的元素
public void replace(int index, int value) {
int oldValue = array[index];
array[index] = value;
// 维护堆的性质
if (value > oldValue) {
up(index);
} else {
down(index);
}
}
// 在堆尾部添加元素
public void add(int value) {
array[size] = value;
size++;
up(size - 1);
}
// 建堆
private void heapify() {
// size/2-1找到非叶子节点
for (int i = size / 2 - 1; i >= 0; i--) {
down(i);
}
}
// 将 parent 索引处的元素下沉:与两个孩子较大者交换,直至没孩子
// 或者孩子没他大
private void down(int parent) {
int left = parent * 2 + 1;
int right = left + 1;
int max = parent;
if (left< size && array[left] > array[max]) {
max = left;
}
if (right< size && array[right] > array[max]) {
max = right;
}
if (max != parent) { // 找到了更大的孩子
swap(max, parent);
down(max);
}
}
// 将 child 索引处的元素上浮:与父节点比较,直至父节点大于等于它
private void up(int child) {
int parent = (child - 1) / 2;
while (child > 0 && array[child] > array[parent]) {
swap(child, parent);
child = parent;
parent = (child - 1) / 2;
}
}
// 交换两个索引
private void swap(int i, int j) {
int t = array[i];
array[i] = array[j];
array[j] = t;
}
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5, 6, 7};
MaxHeap maxHeap = new MaxHeap(arr);
System.out.println(Arrays.toString(maxHeap.array));
maxHeap.add(8);
System.out.println(Arrays.toString(maxHeap.array));
maxHeap.replace(3, 9);
System.out.println(Arrays.toString(maxHeap.array));
maxHeap.poll(2);
System.out.println(Arrays.toString(maxHeap.array));
}
}
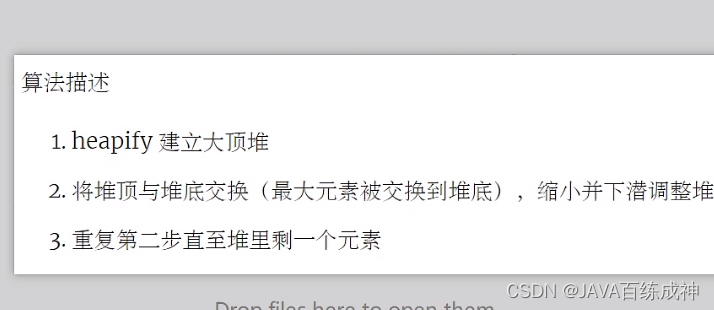
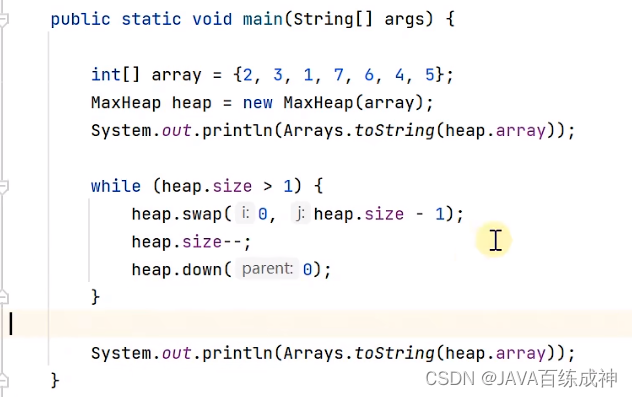
堆排序



![中间件 | RabbitMq - [AMQP 模型]](https://img-blog.csdnimg.cn/direct/01c09f995c1a4d17a8e384fbc40200da.png)