本文是对之前文章“Reeds-Shepp曲线学习笔记及相关思考【点击可跳转】”的补充,因小伙伴的提问,本文补充介绍上述文章第三部分中基础运动公式的推导过程。

本文以上面的第一个公式为例进行介绍,即Reeds-Shepp曲线基础运动中的向前左转运动,其他五个可根据第一个的过程,以此类推。
现假设机器人位于S点处横纵坐标分别为x、y,与x轴夹角为ψ,因此,机器人在S点的状态可以表示为(x,y,ψ),执行L+基础运动前行左转弧长t后,到达G点。求机器人在G点的状态,根据第一个公式可得G点的状态如下:。
G : ( x + sin ( ψ + t ) − sin ( ψ ) , y − cos ( ψ + t ) + cos ( ψ ) , ψ + t ) G:\left(x+\sin(\psi+t)-\sin(\psi),y-\cos(\psi+t)+\cos(\psi),\psi+t\right) G:(x+sin(ψ+t)−sin(ψ),y−cos(ψ+t)+cos(ψ),ψ+t)
现在我们来推导一下这个结果是怎么来的,为方便理解,我绘制了以下示意图,图中大写字母是为了方便对图中的边和角进行描述,图中的小写字母是角度。

G点的第三个状态是与x轴的夹角,执行L+运动之前为ψ, 由于是向前左转,也就是逆时针运动,逆时针运动为正,又因为L+运动向前左转了弧长t,在之前的文章“Reeds-Shepp曲线学习笔记及相关思考【点击可跳转】”中已介绍过计算时会将最小转弯半径归一化为1,即上图中边FG和边FS的长度为1,弧长=弧长圆心角x半径,所以弧长t也对应转过的弧度制角度,因此G点与x轴的夹角为ψ+t
接下来介绍稍微复杂一点的前两个状态的推导过程,由上图容易知道,G点的横纵坐标 x g 、 y g x_g、y_g xg、yg满足下式:
x g = x + G S ∗ cos ∠GSA y g = y + G S ∗ sin ∠GSA ; x_g=x+GS*\text{cos ∠GSA} \hspace{1cm} y_g=y+GS*\text{sin ∠GSA} ; xg=x+GS∗cos ∠GSAyg=y+GS∗sin ∠GSA;
所以我们只要求得边GS的长度和∠GSA即可求得 x g 、 y g x_g、y_g xg、yg
我们先来求边GS,现在我们已知∠GFS=t,边GF=边FS=1,由余弦公式 c 2 = a 2 + b 2 − 2 a b cos γ c^2=a^2+b^2-2ab\cos\gamma c2=a2+b2−2abcosγ得,边GS的长度为:
G S 2 = G F 2 + F S 2 − 2 ∗ G F ∗ F S ∗ cos ∠GFS = 1 + 1 − 2 ∗ cos t = 2 ( 1 − cos t ) GS^2=GF^2+FS^2-2*GF*FS*\text{cos ∠GFS}=1+1-2*\text{cos t}=2(1-\text{cos t}) GS2=GF2+FS2−2∗GF∗FS∗cos ∠GFS=1+1−2∗cos t=2(1−cos t)
由半角公式 sin α 2 = ± 1 − cos α 2 \sin\dfrac{\alpha}{2}=\pm\sqrt{\dfrac{1-\cos\alpha}{2}} sin2α=±21−cosα得,上式可化为:
G
S
2
=
2
(
1
−
cos t
)
=
4
∗
sin
2
t
2
GS^2=2(1-\text{cos t})=4*\sin^{2}\frac{t}{2}
GS2=2(1−cos t)=4∗sin22t
所以:
G S = 4 ∗ sin 2 t 2 = 2 ∗ s i n t 2 GS=\sqrt{4∗\sin^{2}\frac{t}{2}}=2*sin\frac{t}{2} GS=4∗sin22t=2∗sin2t
我们再来求∠GSA,过程如下:
∠GSC=(π–∠GCS)/ 2 = (π–(π–t))/ 2
=
t
2
\text{∠GSC=(π--∠GCS)/ 2 = (π--(π--t))/ 2}= \frac{t}{2}
∠GSC=(π–∠GCS)/ 2 = (π–(π–t))/ 2=2t
∠GSA=∠GSC+∠CSA = t 2 + ψ \text{∠GSA=∠GSC+∠CSA}= \frac{t}{2}+ψ ∠GSA=∠GSC+∠CSA=2t+ψ
将求得的边GS和∠GSA带入,可得G点的横纵坐标 x g 、 y g x_g、y_g xg、yg的表达式:
x g = x + G S ∗ cos ∠GSA = x + 2 ∗ s i n t 2 ∗ cos ( t 2 + ψ ) x_g=x+GS*\text{cos ∠GSA} =x+ 2*sin\frac{t}{2} *\cos \left(\frac{t}{2}+\psi\right) xg=x+GS∗cos ∠GSA=x+2∗sin2t∗cos(2t+ψ)
y g = y + G S ∗ sin ∠GSA = y + 2 ∗ s i n t 2 ∗ sin ( t 2 + ψ ) y_g=y+GS*\text{sin ∠GSA}=y+ 2*sin\frac{t}{2} *\sin \left(\frac{t}{2}+\psi\right) yg=y+GS∗sin ∠GSA=y+2∗sin2t∗sin(2t+ψ)
最后再运用一下如下所示的积化和差公式:
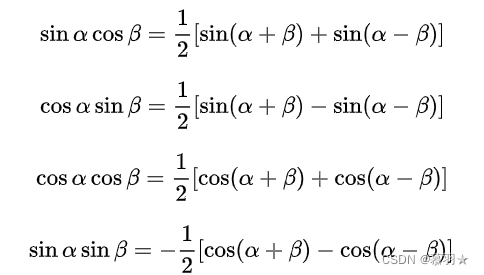
利用积化和差公式,我们可以对 x g 、 y g x_g、y_g xg、yg的表达式进一步化简,如下:
x g = x + 2 ∗ s i n t 2 ∗ cos ( t 2 + ψ ) = x + s i n ( t 2 + t 2 + ψ ) + s i n ( t 2 − t 2 − ψ ) = x + s i n ( t + ψ ) − s i n ( ψ ) x_g=x+ 2*sin\frac{t}{2} *\cos \left(\frac{t}{2}+\psi\right)=x+sin(\frac{t}{2} +\frac{t}{2}+ψ)+sin(\frac{t}{2} -\frac{t}{2}-ψ)=x+sin(t+ψ)-sin(ψ) xg=x+2∗sin2t∗cos(2t+ψ)=x+sin(2t+2t+ψ)+sin(2t−2t−ψ)=x+sin(t+ψ)−sin(ψ)
y g = y + 2 ∗ s i n t 2 ∗ sin ( t 2 + ψ ) = y + c o s ( t 2 − t 2 − ψ ) − c o s ( t 2 + t 2 + ψ ) = y − c o s ( t + ψ ) + c o s ( ψ ) y_g=y+ 2*sin\frac{t}{2} *\sin \left(\frac{t}{2}+\psi\right) =y+cos(\frac{t}{2} -\frac{t}{2}-ψ)-cos(\frac{t}{2} +\frac{t}{2}+ψ)=y-cos(t+ψ)+cos(ψ) yg=y+2∗sin2t∗sin(2t+ψ)=y+cos(2t−2t−ψ)−cos(2t+2t+ψ)=y−cos(t+ψ)+cos(ψ)
到这里,我们已经得到了推导前给出的G点的状态表达式:
G : ( x + sin ( ψ + t ) − sin ( ψ ) , y − cos ( ψ + t ) + cos ( ψ ) , ψ + t ) G:\left(x+\sin(\psi+t)-\sin(\psi),y-\cos(\psi+t)+\cos(\psi),\psi+t\right) G:(x+sin(ψ+t)−sin(ψ),y−cos(ψ+t)+cos(ψ),ψ+t)
也就是,文章开头处给出的第一个Reeds-Shepp曲线的基础运动公式:
L t + ( x , y , ψ ) = ( x + sin ( ψ + t ) − sin ( ψ ) , y − cos ( ψ + t ) + cos ( ψ ) , ψ + t ) L_t^+(x,y,\psi)\quad=\big(x+\sin(\psi+t)-\sin(\psi),y-\cos(\psi+t)+\cos(\psi),\psi+t\big) Lt+(x,y,ψ)=(x+sin(ψ+t)−sin(ψ),y−cos(ψ+t)+cos(ψ),ψ+t)
恭喜小伙伴们(✪ω✪),到这里也就证明,或者说推导就完毕了,有兴趣的小伙伴,可以以此为例子,进行其余五个Reeds-Shepp曲线基础运动公式的推导(ง •_•)ง