题目描述
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
示例 1:
输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。
示例 2:
输入: s = "abab", p = "ab"
输出: [0,1,2]
解释:
起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。
起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。
起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。
提示:
1 <= s.length, p.length <= 3 * 10^4
s 和 p 仅包含小写字母
题解 - 滑动窗口
思路
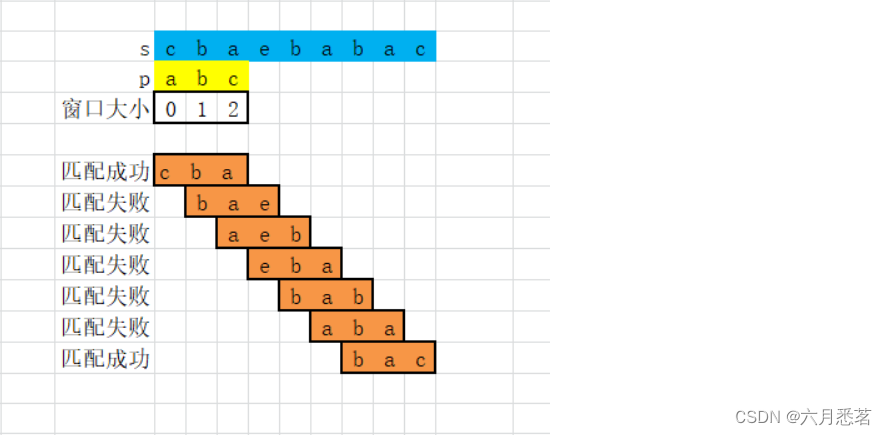
根据题目要求,我们需要在字符串 s 寻找字符串 p 的异位词。因为字符串 p 的异位词的长度一定与字符串 p 的长度相同,所以我们可以在字符串 s 中构造一个长度为与字符串 p 的长度相同的滑动窗口,并在滑动中维护窗口中每种字母的数量;当窗口中每种字母的数量与字符串 p 中每种字母的数量相同时,则说明当前窗口为字符串 p 的异位词。
算法
在算法的实现中,我们可以使用数组来存储字符串 p 和滑动窗口中每种字母的数量。
细节
当字符串 s 的长度小于字符串 p 的长度时,字符串 s 中一定不存在字符串 p 的异位词。但是因为字符串 s 中无法构造长度与字符串 p 的长度相同的窗口,所以这种情况需要单独处理。
代码
/**
* Function to check if a string is a match with a given character array
* @param s: input string
* @param len: length of the input string
* @param vat: character array to match against
* @return true if the string is a match, false otherwise
*/
bool stringIsMatch(char *s, int len, char *vat) {
int i;
char vatBak[26] = {0}; // Array to store character counts of the input string
int temp;
// Count the occurrences of each character in the input string
for (i = 0; i < len; i++) {
// For each character in the string p ,
// the ASCII value of the character is subtracted from the ASCII value of the character 'a'.
// This calculation results in a value between 0 and 25,
// which is used as an index to access the corresponding element in the vat array.
temp = s[i] - 'a';
// After calculating the index temp ,
// the code increments the value stored at index temp in the vat array.
// This effectively counts the occurrences of each character in the string p and stores the counts in the vat array.
vatBak[temp]++;
}
// Compare the character counts with the given character array
for (i = 0; i < 26; i++) {
if (vat[i] != vatBak[i]) {
return false; // If counts don't match, return false
}
}
return true; // If all counts match, return true
}
/**
* Function to find all anagrams of a given string in another string
* @param s: input string
* @param p: string to find anagrams of
* @param returnSize: pointer to store the size of the result array
* @return an array of indices where anagrams are found
*/
int* findAnagrams(char *s, char *p, int *returnSize) {
char vat[26] = {0}; // Array to store character counts of the anagram string
int i;
int temp = 0;
*returnSize = 0;
int *returnNums = (int *)malloc(sizeof(int) * strlen(s)); // Allocate memory for result array
// If the input string is shorter than the anagram string, return empty result
if (strlen(s) < strlen(p)) {
return returnNums;
}
// Count the occurrences of each character in the anagram string
for (i = 0; i < strlen(p); i++) {
temp = p[i] - 'a';
vat[temp]++;
}
// Iterate through the input string to find anagrams
for (i = 0; i <= (strlen(s) - strlen(p)); i++) {
// Check if the substring starting at index i is an anagram
// In the code snippet where `s + i` is used instead of `s[i]` ,
// the expression `s + i` is a pointer arithmetic operation that calculates the memory address of the `i` -th element after the memory address of the base pointer `s` .
// This is because in C, when you add an integer `i` to a pointer `s` ,
// the result is a pointer that points to the memory location `i` elements away from the original memory location pointed to by `s` .
// In this specific context, `s + i` is used to create a pointer
// to a substring of the input string `s` starting from index `i` .
// This pointer is then passed to the `stringIsMatch` function
// to check if this substring is an anagram of the target string `p` .
// By using pointer arithmetic, the code efficiently works with substrings of the input string
// without needing to create a separate substring array,
// thereby optimizing memory usage and performance.
if (stringIsMatch(s + i, strlen(p), vat)) {
returnNums[*returnSize] = i; // Store the index of the anagram
*returnSize = *returnSize + 1; // Increment the size of the result array
}
}
return returnNums; // Return the array of indices where anagrams are found
}