1.脉搏波信号的PRV分析
各类分析参数记参数 意义
| 公式 | 参数意义 | |||
| 线性分析 | 时域分析 | 均值MEAN |
| 反应RR间期的平均水平 |
| 总体标准差SDNN |
| 评估24小时长程HRV的总体变化, SDNN < 50ms 为异常,SDNN>100ms 为正常; | ||
| 均值标准差SDANN |
| 反应HRV中的慢变化成分,异常分界点是40ms。 | ||
| 标准差均值SDNNindex |
| 反应短程(5min)心率的平均变异程度其正常值是81±24ms,异常分界点是 20ms; | ||
| 差值均方的平方根r-MSSD |
| 反映HRV中的快变化成分 | ||
| 相邻间期差值>50ms的百分比(PNN50) |
| 反应RR间期的突然变化,能敏感反应迷走神经的活动。正常分界点为75%. | ||
| 昼夜差值 | 反映平均心率的指数,它是夜间平均 RR 间隔与白天平 均 RR 间隔的差值,这个指数在正常人身上是正值。 | |||
| NN50 | 是全部 RR 间期中相邻的 NN 间 期差大于50ms 的心数,数值越大表明心率变异性愈大。 | |||
| 几何图形 | R间期值直方图 | 反映RR间期的分布情况,横坐标表示RR间期,纵坐标表示RR间期的个数。直方图能较直观反映出RR间期变化的范围及程度,对于正常心率的直方图,一般RR间期在400~100ms之间总心拍比例较大,峰值较突出,与其相应的指标有:SDNN,三角指数,TIRR。 1:三角指数 triangular index)是NN间期总数除以占比例最大的NN间期数,直方图的外形愈宽则三角指数的绝对值愈大,表示心率变异性大,反之偏小; 2:TIRRtriangular interpolation of RR int ernal)是全部RR间期的直方图以峰值为高的近似三角形底边的宽度,其意义与三角指数相同。 | ||
| RR间期差值直方图 | 反映RR间期差异即窦性心律不齐的程度。它是以窦性心搏RR间期长度的差为横坐标,中点为0。后一个RR间期比前个长时,差值为正数;反之,差值为负数。纵坐标为心搏次数。与其相应的指标有: rmSSD,SDSD,PNN50 | |||
| Lorenz散点图 | 以前一心拍RR间期为横坐标,后一心拍RR间期为纵坐标点,依标类推,X轴为RRn,Y轴为RRn+1,定各自的心搏点,构成RR间期散点图。散点图中包含了HRV的线性和非线性的变化趋势,正常人的散点图多集中在45度射线附近,呈彗星状。可通过散点图分析,了解受试者自主神经功能状态。 | |||
| 频域分析 | VLF极低频段(0.0033-0.04hz)的功率 | 机制不明。可能是与体温调节、肾素血管紧张素系统级体液因子等因素有关的长期的调节机制 有关 | ||
| LF低频段(0.04-0.15hz)的功率 | 解释仍然有争议,但是大多数学者认为它是交感神经活动的标志 | |||
| HF高频段(0.15-0.4hz)的功率 | 由迷走神经介导,代表呼吸变异 | |||
| TP信号总功率 | 信号总的变异性 | |||
| LF/HF | 量化交感神经和迷走神经张力的平衡状态 | |||
| 非线性分析 | 分型维数FD | |||
| 功率谱指数 | ||||
| 近似熵ApEn | ||||
| 复杂性测度 |
摘自:心率变异性分析方法的研究进展_王步青,心率变异性的分析方法和应用_刘晓芳
2.采样频率对 PRV 提取方法的影响
信号采样频率的改变会引起脉搏信号主波位置的变化,使提取的 PRV 产生误差。讨论采样频率变化对各方法提取 PRV 信号准确性的影响,找出对采样频率变化不敏感的 PRV 提取方法,对 PRV 信号的准确提取十分重要。
将图 3.13 所示采样频率为 500Hz 的干净仿真脉搏信号,进行降采样,分别降为 250Hz,100Hz,50Hz,25Hz,10Hz 和 6Hz。然后,采用各 PRV 提取方法提取不同采样频率下的脉搏信号中的 PRV 信号,与 TPRV 信号比较,计算它们之间的 MSE,用于评价采样频率变化对 PRV 提取方法的影响。
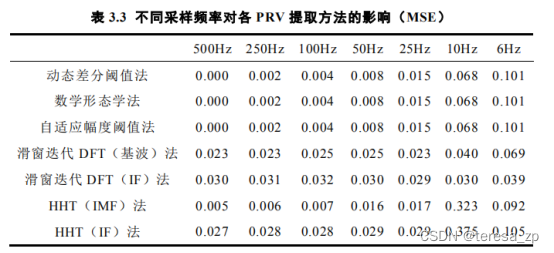
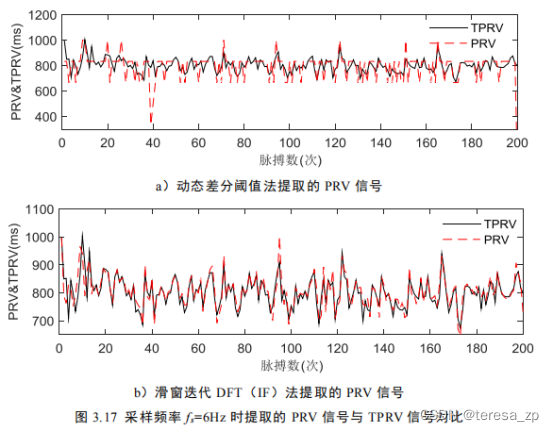
对于不同采样频率下的脉搏信号,由于其中不含噪声,各方法的主波检测准确率 Ac=100%。且随着采样率的降低方法的耗时也在减短。而对于 MSE 变化,如表 3.3 所示,随着采样频率的降低,MSE 在逐渐增加。动态差分阈值法、数学形态学法和自适应幅度阈值法的 MSE 变化趋势相同,由原来 MSE=0 变为0.101,增幅最大。而其它方法的增幅较小,虽然对于采样频率大于 20Hz 脉搏信号中提取的 PRV 信号,其 MSE 比前三种方法大,但其增幅小,说明 MSE 值大是算法本身因素造成的,采样频率的变化对其影响较小。所有方法中,滑窗迭代 DFT(IF)法的 MSE 增幅最小,当采样频率为 6Hz 时,MSE=0.039,误差最小。滑窗迭代DFT(IF)法提取 PRV 信号如图 3.17 中子图 b)所示,相比于动态差分阈值法提取的 PRV 信号,如图 3.17 中子图 a)所示,滑窗迭代 DFT(IF)法提取的 PRV 信号与 TPRV 信号误差最小,受采样频率变化影响较小。
因为滑窗迭代 DFT(IF)法从脉搏基波信号的瞬时频谱中提取 IPRV 信号,其分辨率很高,即使采样频率很低,其仍含有脉搏搏动的信息。而动态差分阈值法、数学形态学法和自适应幅度阈值法以主波检测为基础,滑窗迭代 DFT(基波)法以脉搏信号基波的峰值检测为基础,HHT(IMF)法以 IMF 分量的峰值检测为基础。这些方法都从信号的波形形态中提取 PRV 信号,信号采样频率对脉搏信号波形影响较大,特别是采样频率较小时,使得检测的 PRV 信号与 TPRV 信号间误差很大。虽然 HHT(IF)法也是从频域提取 PRV 信号,其在脉搏信号采样频率大于 10Hz 时,提取 PRV 信号误差一直小于滑窗迭代 DFT(基波)法。可当采样频率继续降低时,提取 PRV 信号误差急剧增加,这是由于 EMD 分解时发生了模态混叠,使获得 IMF 分量含有的主波成分丢失,使提取的 PRV 信号发生失真。
综上所述,对于直接检测脉搏信号主波位置的动态差分阈值法、数学形态学滤波法和本文提出的自适应幅度阈值法,动态差分阈值法对噪声敏感,抗噪性差;数学形态学法耗时较长;相比于这两种方法,自适应幅度阈值法的抗噪性强,实时性高。同时,这三种方法在提取 PRV 信号之前,需要对脉搏信号进行滤波,减少噪声和干扰对脉搏信号主波检测的影响。
对于滑窗迭代 DFT(基波)法和 HHT(IMF)法,其采用含有主波成分的分量信号替代脉搏信号实现 PRV 检测。在没有噪声污染或噪声分布均匀时,EMD分解可以自适应地得到反映主波间期变化的 IMF 分量,从该 IMF 分量提取的 PRV信号比从滑窗迭代 DFT 法得到的基波分量中提取的 PRV 准确性高。但当脉搏信号信噪比降低或噪声分布不均匀时,EMD 分解会产生模态混叠现象,得到的 PRV信号误差很大。同时,EMD 分解过程的反复循环使该方法耗时很长。相比之下,滑窗迭代 DFT 法采用频率分离的方式得到基波信号,并从中提取 PRV 信号,该方法抗噪性强,计算速度快,实时性高。
对于滑窗迭代 DFT(IF)法和 HHT(IF)法,从频域提取 IPRV 信号,比 PRV信号时间分辨率高。滑窗迭代 DFT(IF)可以在低采样频率下(fs=6Hz),准确地提取 PRV 信号。HHT(IF)虽然在低采样频率时发生模态混叠,使得到的 PRV信号误差较大,但在高采样频率时,提取 PRV 信号准确性比滑窗迭代 DFT(IF)法高。就算法实时性而言,滑窗迭代 DFT(IF)法比 HHT(IF)耗时少。但相比滑窗迭代 DFT(基波)和自适应幅度阈值法,耗时仍然很长。
对于动态脉搏信号,从中实时地提取 DPRV 信号,要求 PRV 提取方法准确性和实时性兼顾。通过分析各方法的优缺点,考虑实际脉搏信号信噪比不定,同时,为了保留更多有效信息需要保持较高采样频率等因素,本文采用滑窗迭代 DFT(基波)法从动态脉搏信号中提取 DPRV 信号。
摘自:动态脉搏信号检测与脉率变异性实时分析方法研究_丑永新 博士论文
3.峰谷值查找方法1


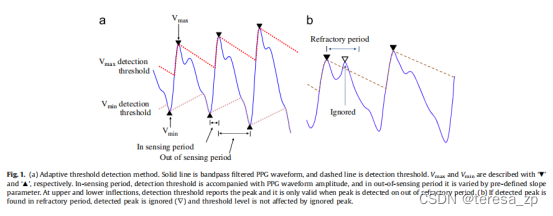
摘自:Adaptive threshold method for the peak detection of photoplethysmographic waveform
4.峰谷值查找方法2
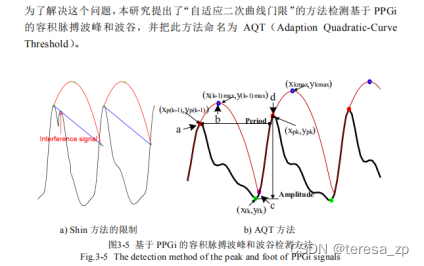
摘自:容积脉搏成像特征提取方法研究及在生理信号检测的应用
5.峰谷值查找方法3
本文开发了一种稳健算法,主要使用PPG衍生物、曲线三角面积(TAOC)、斜率反转和基于时域的轻量级方法的新组合,以揭示PPG开始和收缩峰的精确位置。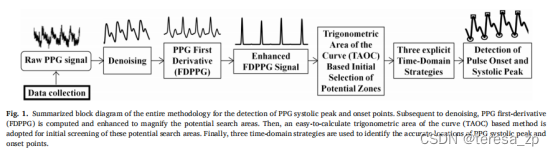
摘自:Efficient and lightweight detection of PPG onset and systolic peaks using implementable time-domain strategies
6.最新(2024)关于PPG信号分析综述类文章
Photoplethysmogram Analysis and Applications:An Integrative Review
7.脉搏波呼吸波峰值点查找方法matlab实现汇总
7.1:hilbert方法
nGzLen = length(Signal);
nGzX = 1:nGzLen;
t=nGzX/fs;
x=(Signal);
nt=t;
Hx=hilbert(x); % 希尔伯特变换
% 作图
figure;
plot(nt, x, 'k', nt,abs(Hx), 'r');
grid; legend('信号', '包络');
xlabel('样点'); ylabel('幅值')
title('信号和包络---hilbert方法')
set(gcf, 'color', 'w');7.2:极值方法
极值方法
x=detrend(Signal);%去直线 基频 看帮助文档
[K1,V1]=v_findpeaks(x,'q',30); % 求极大值位置和幅值
%up=spline(K1,V1,t); % 内插,获取上包络曲线
[K2,V2]=v_findpeaks(x,'v',30);% 求极小值位置和幅值
%down=spline(K2,V2,t); % 内插,获取下包络曲线
up = interp1(K1/fs,V1,t, 'pchip'); %分段三次hermite
down = interp1(K2/fs,V2,t,'pchip');
amp=up-down;
Vamp=V1(2:end)-V2;
Vinx=(K1(2:end)+K2)/2;
amp2 = interp1(Vinx/fs,Vamp,t,'linear');
figure;
subplot(2,1,1);
% plot(t,CO2_1,'b');
% hold on;
plot(t,x,'k');
hold on;
grid;
plot(K1/fs,V1,'r*');
hold on
plot(K2/fs,V2,'r*');
hold on
plot(t,up,'r');
hold on
plot(t,down,'r');
hold on
xlabel('样点'); ylabel('幅值');
title('用求取极大极小值方法获取包络曲线图 极值方法')
set(gcf,'color','w');
subplot(212)
plot(t,amp,'b');
hold on
grid on
plot(t,amp2,'r');
hold on
plot(Vinx/fs,Vamp,'r*');
hold on 7.3:envelope取包络方法
x=detrend(Signal);%去直线 基频 看帮助文档
[up,down] = envelope(t,x,'pchip');% 分段三次hermite
amp=up-down;
% 作图
figure;
subplot(2,1,1);
plot(t,x,'k',t,up,'r',t,down,'g');
xlabel('样点'); ylabel('幅值'); grid;
title('调用envelope函数求取上下包络曲线图')
set(gcf,'color','w');
subplot(2,1,2);
plot(t,amp,'g');
xlabel('样点'); ylabel('幅值'); grid;
title('幅度')
set(gcf,'color','w');7.4:平方后低通方法
平方后低通方法
CO2_pow2=power(Signal,2);
DEN=[1,-7.79606779210506,26.5932120482461,-51.8404844176109,63.1666773411061,-49.2637313165491,24.0152170393195,-6.69032514934920,0.815502246948220];
NUM=[2.21680664897793e-14,1.77344531918235e-13,6.20705861713822e-13,1.24141172342764e-12,1.55176465428455e-12,1.24141172342764e-12,6.20705861713822e-13,1.77344531918235e-13,2.21680664897793e-14];
filterdata=filter(NUM,DEN,CO2_pow2);%低通2hz iir butterworth 400采样率
filterdata1=sqrt(filterdata./0.5);
figure;
subplot(211);
plot(CO2_pow2);
grid on
hold on ;
subplot(212);
plot(filterdata1, 'b');
grid on
title('平方后低通方法');7.5:EMD方法
[imf,residual,info]=emd(Signal,'INTERP','spline' );
figure;
title('emd方法');
subplot(4,1,1);
plot(imf(1,:));
grid on ;
subplot(4,1,2);
plot(imf(2,:));
grid on ;
subplot(4,1,3);
plot(imf(3,:));
grid on ;
subplot(4,1,4);
plot(imf(4,:));
grid on ;
figure;
subplot(4,1,1);
plot(imf(5,:));
grid on ;
subplot(4,1,2);
plot(imf(6,:));
grid on;
subplot(4,1,3);
plot(imf(7,:));
grid on ;
subplot(4,1,4);
plot(imf(8,:));
grid on ;