目录
1.图的相关概念
2.图的存储
2.1.直接存法
1.查询是否存在某条边
2.遍历一个点的所有出边
3..遍历整个图
应用
2.2.邻接矩阵
1.查询是否存在某条边
2.遍历一个点的所有出边
3..遍历整个图
应用
2.3.邻接表
1.查询是否存在某条边
2.遍历一个点的所有出边
3..遍历整个图
应用
2.4.链式前向星
应用
1.图的相关概念
在图论中,有一些核心概念和基本术语,这些概念对于理解和处理图结构非常重要。以下是一些常见的图论概念梳理:
有向图:
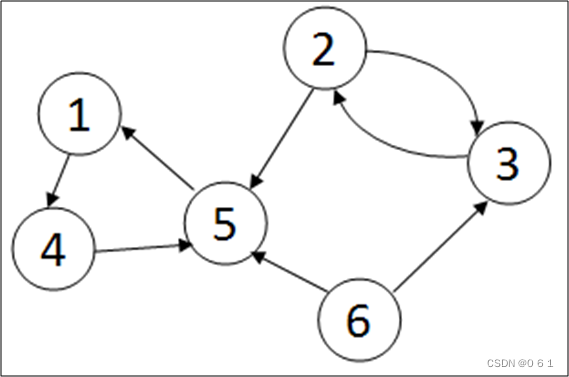
无向图:
1.图 (Graph):图是由点集合及连接这些点的边集合组成的数学结构。图的点通常称为“顶点”(vertices),而连接顶点的线或弧称为“边”(edges)。
2.简单图 (Simple graph)与完全图:简单图是没有重复边和重复顶点的图。也就是说,在简单图中,任何两个不同的顶点之间最多只有一条边,并且不存在顶点到边,除了自环。完全图是一种简单图,其中任意两个不同的顶点之间都有一条边。
3.自环 (Loop):自环是指顶点自身相连的边。即一个顶点与自身的一条边。
4.重边:重边是指在图中连接相同两个顶点的边,如果有两条或多条边连接同一个顶点对,则这些边称为重边。
5.点边关联:点边关联是指图中的每个顶点都与零条或多条边相关联。
6.边相邻,点相邻:边相邻:如果两条边共享一个顶点,则这两条边是边相邻的。点相邻:如果两个顶点之间存在一条边,则这两个顶点是点相邻的。
7.度 (Degree):顶点的度是指与该顶点相邻的边的数量。即连接到该顶点的边的条数。
8.孤立点 (Isolated vertex):孤立点是指度为零的顶点,即没有与其他顶点相连的顶点。
9.叶节点 (Leaf vertex):叶节点,也称为终端节点,是指度为1的顶点,即只与一个顶点相连的顶点。
10.偶点 (Even vertex):偶点是指度的度数为偶数的顶点。
11.奇点 (Odd vertex):奇点是指度的度数为奇数的顶点。
12.最小度 (Minimum degree):最小度是指图中所有顶点中最小的度值。
13.最大度 (Maximum degree):最大度是指图中所有顶点中最大的度值。
14.出度 (Outdegree)与入度 (Indegree):出度是指从某个顶点出发的边的数量,入度是指指向某个顶点的边的数量。
15. k−正则图k−Regular Graph):k−正则图是指所有顶点的度都是k的图。
16.同构 (Isomorphism):如果两个图在结构上完全相同,即它们具有相同的顶点和边,并且这些边连接相同的顶点对,那么这两个图是同构的。
17.途径 (Walk):图中的一条路径是一系列顶点的序列,其中每一对相邻顶点之间都有一条边或弧。路径可以有方向或无方向。
18.迹 (Trail):迹是图中的一条路径,除了允许重复经过相同的边,不允许经过相同的顶点。
19.路径 (Path):路径是图中的一条无重复边的序列,每个顶点只一次,除了第一个和最后一个顶点。
20.回路 (Circuit)与简单回路 (Simple circuit)
- 回路或环是指从一个顶点出发,经过一系列边和顶点,最终回到出发点的路径。
- 简单回路是指没有重复边和顶点的回路。
21.图的连通性 (Connected)与连通图 (Connected graph)以及连通分量 (Connected component)
- 连通性是指图中任意两个顶点之间都存在一条路径。
- 连通图是指图中任意两个顶点都是连通的。
- 连通分量是指在一个图中,所有连通顶点的集合。
22.导出子图/诱导子图 (Induced subgraph):导出子图是指原图中由一组顶点和它们之间的边组成的子图,而诱导子图是指原图中由一组顶点所形成的子图及其所有相邻边。
23.补图:补图是指原图的所有顶点以及原图中没有的边组成的图。
24.一些特殊的无向简单图
- 星图:一个中心顶点和其余顶点连接而成的图。
- 圈图:一个闭合的顶点序列,每个顶点都与其他顶点相连。
25.无向简单图有关的二元运算(交、并、和、笛卡尔积)
- 交(Intersection):图G和H的交是由G和H中共同的边组成的图。如果两条边在G和H中都存在,那么它们也存在于交图中。
- 并(Union):图G和H的并是由G和H中的所有边组成的图,包括G中的边和H中的边,但不包括G和H的交中的边。
- 和(Symmetric Difference):图G和H的和是由G和H中不共同的边组成的图。如果一条边在G中但不在H中,或者在H中但不在G中,那么这条边就在和图中。
- 笛卡尔积(Cartesian Product):图G和H的笛卡尔积是由G的每个顶点与H的每个顶点相连组成的图。如果G有v个顶点,H有w个顶点,那么G和H的笛卡尔积有vw个顶点,每个顶点都是由一个来自G的顶点和一个来自H的顶点组成的。
26.点割集与边割集
- 点割集:如果移除图中的一个顶点,会导致原图不再连通,那么这个顶点就是一个点割。所有这样的顶点的集合称为点割集。
- 边割集:如果移除图中的一条边会导致原图不再连通,那么这条边就是一个边割。所有这样的边的集合称为边割集。
27.树、森林、最小生成树
- 树是一种没有环的无向图,它是连通的,并且有n个顶点就有n-1条边。
- 森林是由零个或多个树组成的图。
- 最小生成树是指在一个加权连通图中,权值之和最小的生成树。
28.最短路径
- 最短路径是指在加权图中,连接两个顶点的路径中权值之和最小的路径。
29.拓扑排序
- 拓扑排序是指对有向无环图(DAG)的所有顶点进行排序,使得对于图中的每条有向边(u,v),顶点u在排序中顶点v之前。这样的排序是唯一的,如果存在多个DAG可以有多个拓扑排序。
2.图的存储
2.1.直接存法
使用一个数组来存边,数组中的每个元素都包含一条边的起点与终点(带边权的图还包含边权)(或者使用多个数组分别存起点,终点和边权)。空间复杂度:O(m)。
struct Edge {
int u, v;
};
vector<Edge> e;
1.查询是否存在某条边
struct Edge {
int u, v;
};
vector<Edge> e;
int m;//有m条边
bool find_edge(int u, int v) {
for (int i = 1; i <= m; i++) {
if (e[i].u == u && e[i].v == v) {
return true;
}
}
return false;
}算法复杂度为:O(m);
2.遍历一个点的所有出边
struct Edge {
int u, v;
};
vector<Edge> e;
int m;//有m条边
void find_outedge(int u) {
for (int i = 1; i <= m; i++) {
if (e[i].u == u) {
//对这个点的出边的操作
}
}
}算法复杂度:O(m);
3..遍历整个图
struct Edge {
int u, v;
};
vector<Edge> e;
int m, n;//m条边,n个点
vector<bool> vis(n + 1, false);
void dfs(int u) {
if (vis[u]) return;//访问过返回
vis[u] = true;//u访问过
for (int i = 1; i <= m; i++) {
if (e[i].u == u) {
dfs(e[i].v);//递归遍历下一个节点
}
}
}![]() 算法复杂度:O(nm);
算法复杂度:O(nm);
应用
由于直接存边的遍历效率低下,一般不用于遍历图。
在 Kruskal 算法 Kruskal 算法中,由于需要将边按边权排序,需要直接存边。
在有的题目中,需要多次建图(如建一遍原图,建一遍反图),此时既可以使用多个其它数据结构来同时存储多张图,也可以将边直接存下来,需要重新建图时利用直接存下的边来建图。
2.2.邻接矩阵
使用一个二维数组 adj 来存边,其中 adj[u][v] 为 1 表示存在u到v的边,为 0 表示不存在。如果是带边权的图,可以在 adj[u][v] 中存储u到b的边的边权。空间复杂度:O() 。
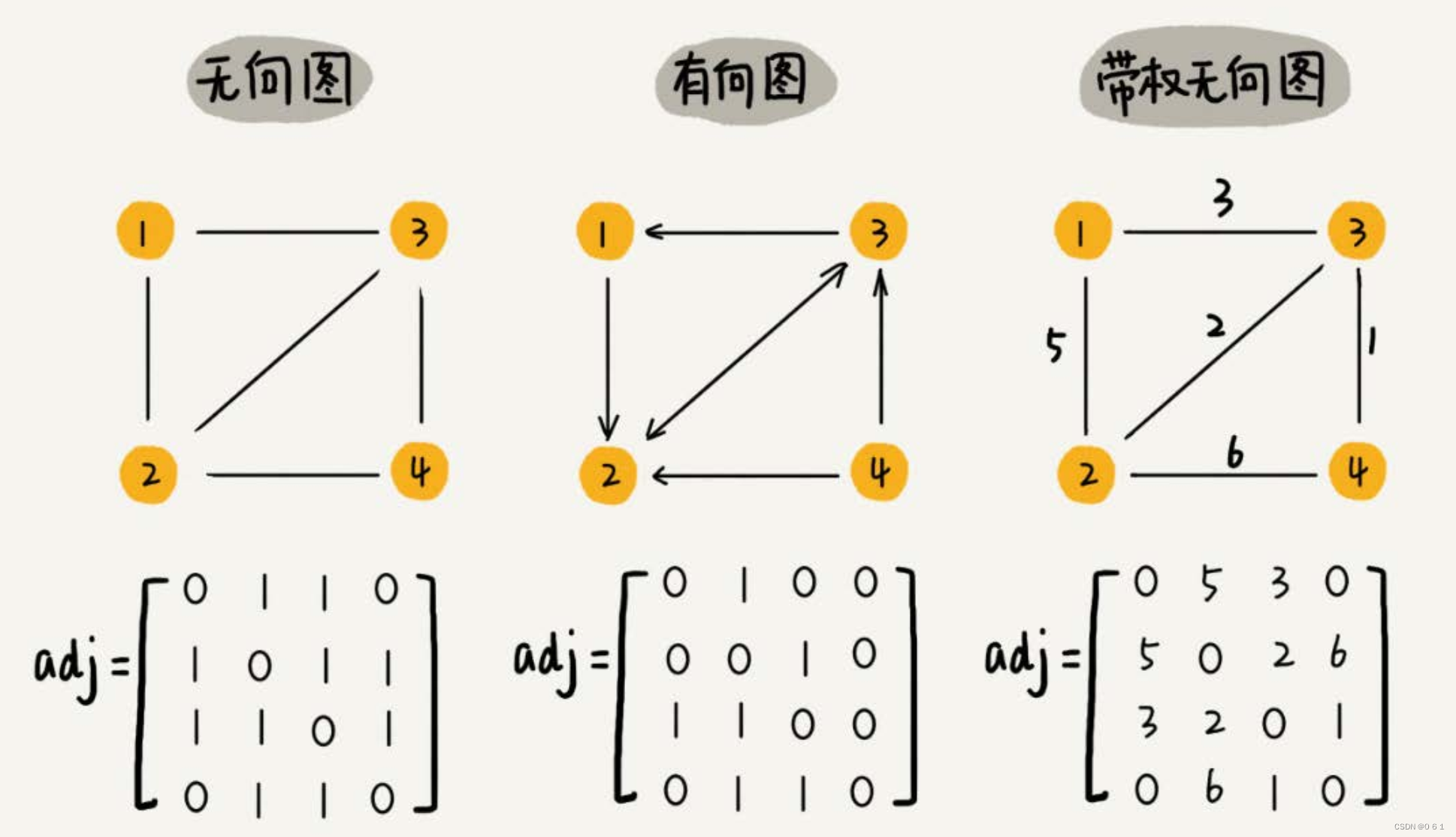
vector<vector<bool> > adj;1.查询是否存在某条边
vector<vector<bool> > adj;
bool find_edge(int u, int v) { return adj[u][v]; }算法复杂度为:O(1);
2.遍历一个点的所有出边
struct Edge {
int u, v;
};
vector<vector<bool> > adj;
int n;//有n个点
void find_outedge(int u) {
for (int i = 1; i <= n; i++) {
if (adj[u][n]) {
//对这个点的出边的操作
}
}
}算法复杂度:O(n);
3..遍历整个图
int m, n;//m条边,n个点
vector<bool> vis(n + 1, false);
vector<vector<bool> > adj;
void dfs(int u) {
if (vis[u]) return;//访问过返回
vis[u] = true;//u访问过
for (int v = 1; v <= n; i++) {
if (adj[u][v]) {
dfs(v);//递归遍历下一个节点
}
}
}![]() 算法复杂度:O(
算法复杂度:O();
应用
邻接矩阵只适用于没有重边(或重边可以忽略)的情况。
其最显著的优点是可以O(1)查询一条边是否存在。
由于邻接矩阵在稀疏图上效率很低(尤其是在点数较多的图上,空间无法承受),所以一般只会在稠密图上使用邻接矩阵。
2.3.邻接表
使用一个支持动态增加元素的数据结构构成的数组,如 vector<int> adj[n + 1] 来存边,其中 adj[u] 存储的是点u的所有出边的相关信息(终点、边权等)。空间复杂度:O(m)。用代指点v的出度,即以v为出发点的边数。
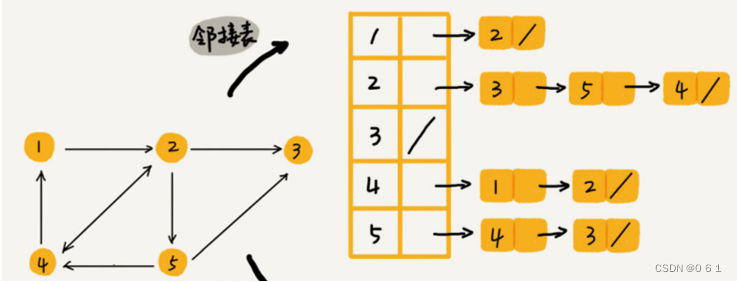
vector<vector<int> > adj;//以存终边为例 1.查询是否存在某条边
vector<vector<int> > adj;//以存终边为例
bool find_edge(int u, int v) {
for (int i = 0; i < adj[u].size(); i++) {
if (adj[u][i] == v) {
return true;
}
}
return false;
}算法复杂度为:O();(如果事先进行了排序就可以使用二分查找做到O(log(
))。
2.遍历一个点的所有出边
vector<vector<int> > adj;//以存终边为例
void find_outedge(int u) {
for (int i = 0; i < adj[u].size(); i++) {
adj[u][i]//对这个点的出边的操作
}
}算法复杂度:O();
3..遍历整个图
int m, n;//m条边,n个点
vector<bool> vis(n + 1, false);
vector<vector<int> > adj;
void dfs(int u) {
if (vis[u]) return;//访问过返回
vis[u] = true;//u访问过
for (int i = 0; i < adj[u].size(); i++) dfs(adj[u][i]);//递归遍历下一个节点
}![]() 算法复杂度:O(n + m);
算法复杂度:O(n + m);
应用
存各种图都很适合,除非有特殊需求(如需要快速查询一条边是否存在,且点数较少,可以使用邻接矩阵)。
尤其适用于需要对一个点的所有出边进行排序的场合。
2.4.链式前向星
本质上是用链表实现的邻接表,核心代码如下:
// head[u] 和 cnt 的初始值都为 -1
void add(int u, int v) {
nxt[++cnt] = head[u]; // 当前边的后继
head[u] = cnt; // 起点 u 的第一条边
to[cnt] = v; // 当前边的终点
}
// 遍历 u 的出边
for (int i = head[u]; i != -1; i = nxt[i]) {
int v = to[i];
}#include <iostream>
#include <vector>
using namespace std;
int n, m;
vector<bool> vis;
vector<int> head, nxt, to;
void add(int u, int v) {
nxt.push_back(head[u]);
head[u] = to.size();
to.push_back(v);
}
bool find_edge(int u, int v) {
for (int i = head[u]; i != -1; i = nxt[i]) {
if (to[i] == v) {
return true;
}
}
return false;
}
void dfs(int u) {
if (vis[u]) return;
vis[u] = true;
for (int i = head[u]; i != -1; i = nxt[i]) dfs(to[i]);
}
int main() {
cin >> n >> m;
vis.resize(n + 1, false);
head.resize(n + 1, -1);
for (int i = 1; i <= m; ++i) {
int u, v;
cin >> u >> v;
add(u, v);
}
return 0;
}各个算法复杂度与邻接矩阵相同
应用
存各种图都很适合,但不能快速查询一条边是否存在,也不能方便地对一个点的出边进行排序。
优点是边是带编号的,有时会非常有用,而且如果 cnt 的初始值为奇数,存双向边时 i ^ 1 即是 i 的反边(常用于网络流)。