🍉CSDN小墨&晓末:https://blog.csdn.net/jd1813346972
个人介绍: 研一|统计学|干货分享
擅长Python、Matlab、R等主流编程软件
累计十余项国家级比赛奖项,参与研究经费10w、40w级横向
文章目录
- 1 加载相关包
- 2 对数收益率可视化
- 2.1 对数收益率时序可视化
- 2.2 对数收益率直方图
- 3 正态分布拟合
- 3.1 拟合均值及标准差
- 3.2 拟合AIC值
- 3.3 拟合密度估计值及对数收益率范围
- 3.4 拟合经验密度及正态分布曲线
- 4 假设检验
- 4.1 t检验
- 4.2 偏度t统计量
- 4.3 偏度P值
- 4.4 峰度t统计量
- 4.5 正态分布检验
该篇文章实现了对深证综指收益率数据进行分布拟合,首先对原始数据进行对数收益率计算,然后实现对数收益率数据的时序可视化及直方图展示。然后完成正态分布拟合的相关操作:均值;标准差;AIC值;密度估计值;对数收益率范围;经验密度及正态分布曲线。最后对对数收益率数据进行相关检验操作:t检验、偏度统计量计算及偏度检验;峰度统计量计算及峰度检验;正态分布检验。

1 加载相关包
rm(list=ls()) #清空变量
library("openxlsx") #加载包
library("knitr") #加载包
library("xlsx") #加载包
library("tseries") #加载包
2 对数收益率可视化
2.1 对数收益率时序可视化
运行程序:
#加载包
data<-read.xlsx("F:\\2021-03-15 上证指数,深证综指日交易数据.xls",'Sheet1',
encoding ="UTF-8")#读取数据
rt=log(data$收盘价.元.点._ClPr)-log(data$昨收盘.元.点._PrevClPr)#对数收益率
rt=na.omit(rt) #清除缺失数据
rt1=ts(rt,start =c(1991,4,4),frequency = 244) #转化为时序数据
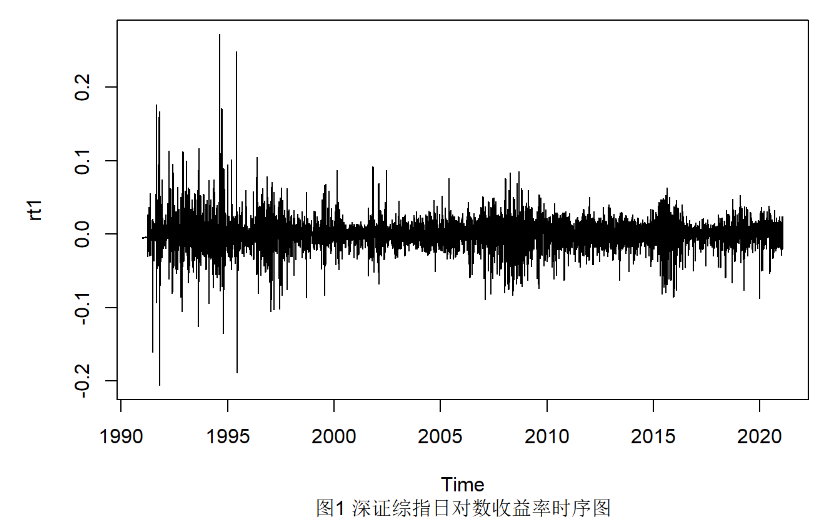
plot(rt1,sub="图1 深证综指日对数收益率时序图")
运行结果:
首先由收益率公式:
r t = l n P t P t − 1 = l n P t − l n P t − 1 r_t=ln \frac{P_t}{P_{t-1}}=lnP_t-lnP_{t-1} rt=lnPt−1Pt=lnPt−lnPt−1
计算深证综指日对数收益率,并对缺失值进行处理,得到从1991-2021年深证综指的对数收益率共7379个观测值。由于该证券数据一年多为244天,故以244天作为1年绘制证券收益率时序图(图1),接下来利用清洗过后的数据进行其分布拟合。
2.2 对数收益率直方图
运行程序:
library(MASS)#加载包
hist(rt,nclass = 30,sub="图2 1991-2021年深证综指的对数收益率直方图") #1991-2021年深证综指的对数收益率直方图
运行结果:
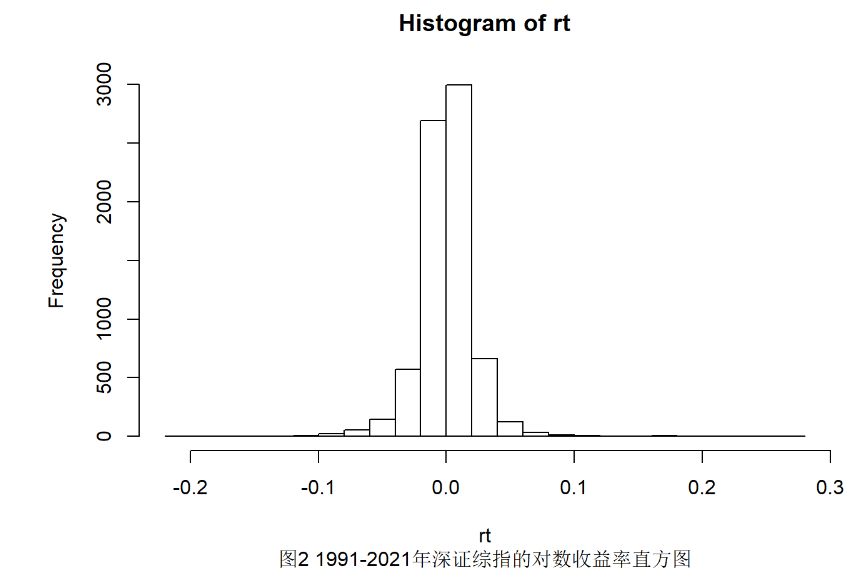
图2显示1991-2021年深证综指的对数收益率直方图,它通过将数据划分为30个子区间而得到。由图2可知,日对数收益率曲线关于它的零均值近似对称。
3 正态分布拟合
3.1 拟合均值及标准差
运行程序:
fit1=fitdistr(rt1,densfun = "normal") #拟合正态分布
E=fit1$estimate
E #拟合均值及标准差
运行结果:
## mean sd
## 0.0004303541 0.0214256749
3.2 拟合AIC值
运行程序:
AIC(fit1) #AIC值
运行结果:
## [1] -35559.41
3.3 拟合密度估计值及对数收益率范围
运行程序:
d1=density(rt1) #获得密度估计值
range(rt1) #深证综指的对数收益率范围
运行结果:
## [1] -0.2061087 0.2722098
3.4 拟合经验密度及正态分布曲线
运行程序:
x=seq(-.2,.2,by=0.001)
y1=dnorm(x,E[1],E[2]) #输出满足正态分布的概率密度值
plot(d1$x,d1$y,xlab="rtn",ylab="density",type="l",sub="图3 日对数收益率的经验密度曲线及正态分布密度曲线")
lines(x,y1,col=2,lty=2) #对数收益率的经验密度函数及正态分布的密度函数
运行结果:

其中黑色线曲线为日对数收益率的经验密度曲线,红色虚线曲线为拟合的正态分布的密度曲线。
4 假设检验
4.1 t检验
运行程序:
library(fBasics)
t.test(rt) #在0.05的显著性水平下,均值为0
运行结果:
##
## One Sample t-test
##
## data: rt
## t = 1.7201, df = 7334, p-value = 0.08545
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## -0.0000600836 0.0009207918
## sample estimates:
## mean of x
## 0.0004303541
4.2 偏度t统计量
运行程序:
s3<-skewness(rt)[1]
t<-length(rt)
t3<-s3/sqrt(6/t)
t3 #偏度t统计量
运行结果:
## [1] 13.39004
4.3 偏度P值
运行程序:
pp<-2*(1-pnorm(t3))
pp #偏度p值,小于0.05,拒绝原假设
运行结果:
## [1] 0
4.4 峰度t统计量
运行程序:
s4<-kurtosis(rt)[1]
t4<-s4/sqrt(24/t) #峰度t统计量
t4 #值是巨大的,拒绝原假设,有厚尾部
运行结果:
## [1] 246.7373
4.5 正态分布检验
运行程序:
normalTest(rt,method = "jb") #p<0.05,拒绝原假设
运行结果:
##
## Title:
## Jarque - Bera Normalality Test
##
## Test Results:
## STATISTIC:
## X-squared: 61098.91
## P VALUE:
## Asymptotic p Value: < 2.2e-16
拟合正态分布得到估计均值为0.00043,估计标准差为0.021。且AIC值为-35559.41,具有较好的拟合度。图3的实线列出了深证综指的日对数收益率的经验密度函数,通过用非参数的平滑方法得到。图3的红色虚线显示了深证综指的日对数收益率正态分布的密度函数,它们具有相同的均值和标准差,根据图3可以看到,和正态分布相比,经验密度函数具有更高的峰值和更厚的尾部。表明深证综指的日对数收益率是非正态的。结合正态性检验发现,JB检验的p值为 2.2 × 1 0 − 6 2.2×10^{-6} 2.2×10−6,远小于0.05,在0.05的显著性水平下拒绝服从正态分布的原假设,表明经验密度函数结果与正态性检验结果一致。