简介:
2014年Ian Goodfellow提出以来,GAN就存在着训练困难、生成器和判别器的loss无法指示训练进程、生成样本缺乏多样性等问题。从那时起,很多论文都在尝试解决,但是效果不尽人意,比如最有名的一个改进DCGAN依靠的是对判别器和生成器的架构进行实验枚举,最终找到一组比较好的网络架构设置,但是实际上是治标不治本,没有彻底解决问题。
2017年Martin Arjovsky提出了 Wasserstein GAN(下面简称WGAN)成功解决了GAN的系列问题:
1 彻底解决GAN训练不稳定的问题,不再需要小心平衡生成器和判别器的训练程度
2 基本解决了collapse mode的问题,确保了生成样本的多样性
3 训练过程中终于有一个像交叉熵、准确率这样的数值来指示训练的进程,这个数值越小代 表GAN训练得越好,代表生成器产生的图像质量越高
WGAN 里面比较难以理解的是EMD和WGAN 损失函数的关系,以及理论证明
这个会在理论二单独证明.
目录
1 GAN
2 WGAN
3 WGAN 理论
一 GAN 问题
GAN 使用了BCE loss, 根据生成器的损失函数差异: 有两种方案
2.1
总体损失函数:
生成器G的优化目标:
问题
不重叠的时候,
,为常数,梯度为0,无法优化生成器G. 备注:
当
与
的支撑集(support)是高维空间中的低维流形(manifold)时,
与
重叠部分测度(measure)为0的概率为1。
是由低维的流形(随机噪声输入)映射到高维空间的
- 支撑集(support)其实就是函数的非零部分子集,比如ReLU函数的支撑集就是(0,+∞),一个概率分布的支撑集就是所有概率密度非零部分的集合。
- 流形(manifold)是高维空间中曲线、曲面概念的拓广,我们可以在低维上直观理解这个概念,比如我们说三维空间中的一个曲面是一个二维流形,因为它的本质维度(intrinsic dimension)只有2,一个点在这个二维流形上移动只有两个方向的自由度。同理,三维空间或者二维空间中的一条曲线都是一个一维流形。
- 测度(measure)是高维空间中长度、面积、体积概念的拓广,可以理解为“超体积
2.2
生成器G的优化目标:
这个等价最小化目标存在两个严重的问题。第一是它同时要最小化生成分布与真实分布的KL散度,却又要最大化两者的JS散度,一个要拉近,一个却要推远!在数值上则会导致梯度不稳定,这是后面那个JS散度项的毛病。 这就是mode collapse 问题
二 WGAN
2.1 模型

生成器G
输入
随机噪声z
输出:
鉴别器D:
输入:
一种是采样自训练集中的
2.2 损失函数

,
GAN 输出的是一个0,1之间的概率
WGAN 输出的一个scalar
对于鉴别器D:
输入训练图片,希望
尽量大
输入生成图片,希望
尽量小,
2.3 跟GAN区别
- 1 判别器最后一层去掉sigmoid
- 2 生成器和判别器的loss不取log
- 训练技巧:
- 1 每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c
- 2 不要用基于动量的优化算法(包括momentum和Adam),推荐RMSProp,SGD也行
2.4 训练方法
\
三 理论分析
WGAN 的理论基础是Wasserstein Distance,也叫推土机距离, Kantorovich-Rubinstein 算法.
本篇我们重点讲两个
1: 什么是 Wasserstein Distance
2: Wasserstein Distance 怎么变换到WGAN 的损失函数
3.1 Wasserstein Distance
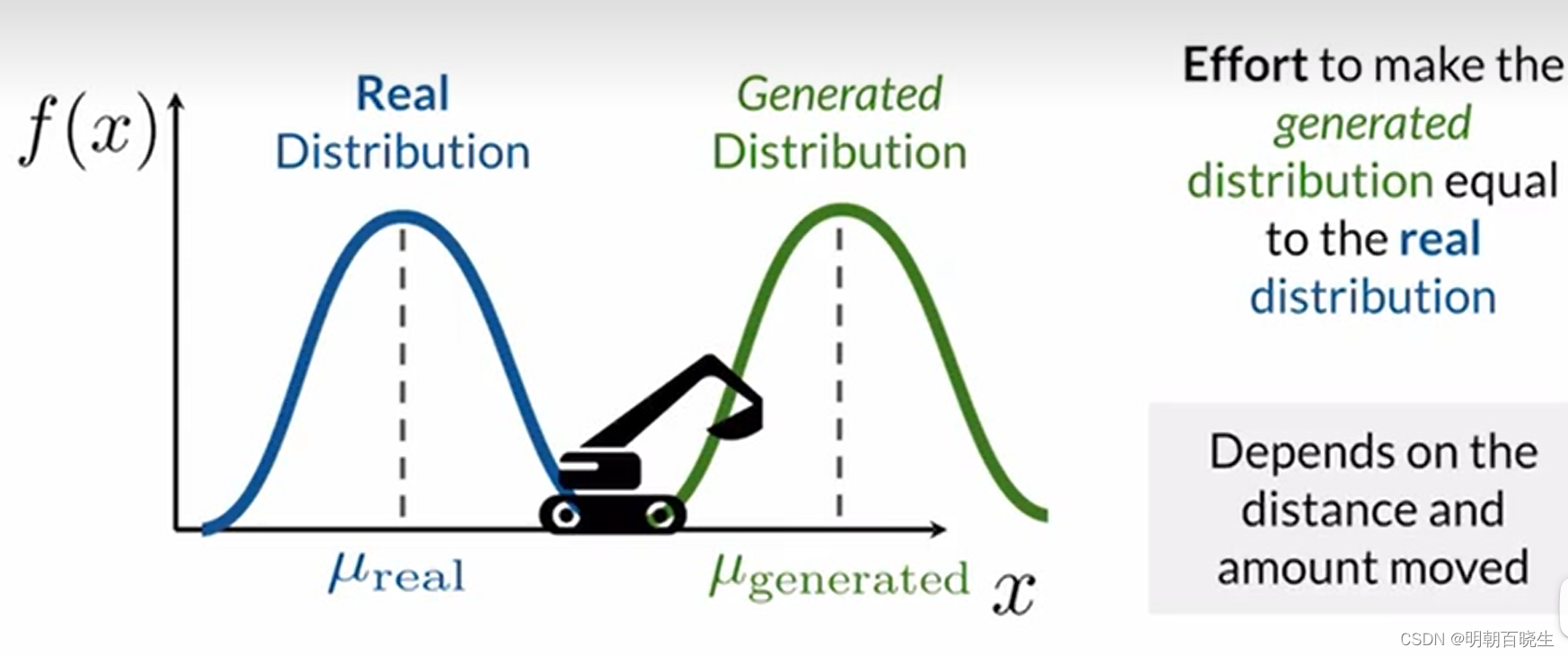
Wasserstein Distance也称为推土机距离(Earth Mover’s distance, EMD),Wasserstein Distance的定义是评估由P分布转换成Q分布所需要的最小代价(移动的平均距离的最小值).
代价取决于两个因素: 移动的距离以及移动大小
定义:
我们下面举个例子,帮助理解该函数:
3.2 例子

如上图:
生成图像的概率密度函数是
真实图像的概率密度函数是
传输方案一(Transport plan 1 标记 )
我们把的概率 :
移动0.1 至 移动0.4 至
我们把的概率 :
移动0.1 至 , 移动0.4 至
我们可以用矩阵表示

其EMD 距离为
传输方案二(Transport plan 2 标记 )
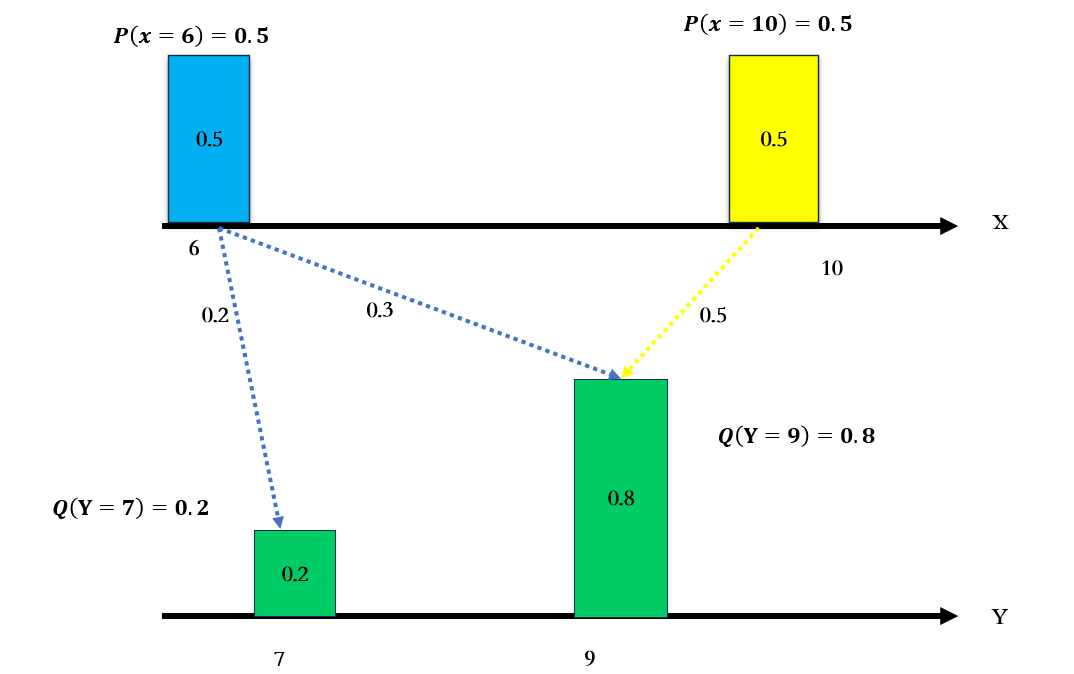
我们把的概率 :
移动0.2 至 移动0.3 至
我们把的概率 :
移动0.5 至
我们可以用矩阵表示

因为方案2 , 所以
更好,实际上我们真实图像的分布复杂度远远比
该分布复杂,对应的传输方案也有无数种,深度学习的目标就是借助神经网络,
从该方案中找到最优的方案
参考
1 WAGAN 论文: https://arxiv.org/pdf/1701.07875.pdf2 WGAN基本原理及Pytorch实现WGAN-CSDN博客
3 earth-movers-distance_哔哩哔哩_bilibili
4 https://www.youtube.com/watch?v=3JP-xuBJsyc&t=2644s
5 令人拍案叫绝的Wasserstein GAN - 知乎
6 Introduction to the Wasserstein distance_哔哩哔哩_bilibili
7 https://www.youtube.com/watch?v=xs9uibPODGk
8 Wasserstein GAN and the Kantorovich-Rubinstein Duality - Vincent Herrmann