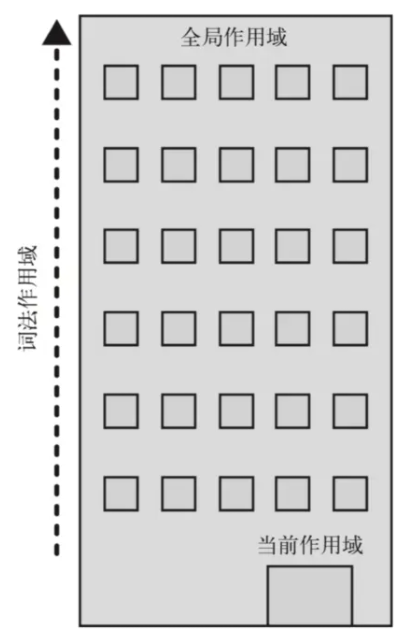
1.递归函数

• 递归函数：函数自己调用自己

2.需求

• 使用函数的方式，计算数字n的阶乘

# 5！
"""
5! = 1 * 2 * 3 * 4 * 5
4! = 1 * 2 * 3 * 4
3! = 1 * 2 * 3
2! = 1 * 2
1! = 1

综上可以总结出：n! = n * (n - 1)
"""

"""
实现递归的思路：
1.找到临界值（临界条件）：1!= 1
2.找到两个循环间的关系
3.总结规律：n! = n * (n - 1)
"""
def digui(n):
    if n == 1:
        return 1
    return n * digui(n - 1)

print(digui(5))

3.练习

• 封装函数，使用递归实现传入一个数字m，得到第m个斐波拉契数列的数字

• 斐波拉契数列前两个数字是1，从第三个数字开始，后面的数字是前面的两个数字的和，例如：1 1 2 3 5 8 13 21 34 55 89 ......

def fn(m):
    if m < 3:
        return 1
    return fn(m - 1) + fn(m - 2)
print(fn(6))

4.总结

该文章介绍了递归函数的概念和实现方式，包括阶乘和斐波那契数列的递归实现。阶乘的递归实现通过找到临界值和两个循环间的关系，总结出n!=n*(n-1)的规律。斐波那契数列的递归实现则是通过封装函数，传入一个数字m，得到第m个斐波拉契数列的数字。