目录
什么是动态规划算法
如何判断题目中将使用动态规划算法?
动态规划题目做题步骤
动态规划题目解析
泰波那契数模型
第 N 个泰波那契数
三步问题
使用最小花费爬楼梯
路径问题
不同路径
不同路径 Ⅱ
珠宝的最高价值
下降最短路径和
地下城游戏
简单多状态问题
按摩师
打家劫舍 Ⅱ
删除并获得点数
粉刷房子
复杂多状态问题
买卖股票的最佳时机含冷冻期
买卖股票的最佳时机含手续费
买卖股票的最佳时机 Ⅲ
买卖股票的最佳时机 Ⅳ
子数组问题
最大子数组和
环形子数组的最大和
乘积最大数组
什么是动态规划算法
动态规划(Dynamic programming)是一种通过把原问题分解为相对简单的子问题的方式求解复杂问题的算法。 动态规划常常适用于有重叠子问题和最优子结构性质的问题,动态规划方法所耗时间往往远少于朴素解法。
如何判断题目中将使用动态规划算法?
当分析问题的过程中,出现重复子问题,例如下面的问题:
三步问题
小孩多次重复上楼这个动作,问最多的方式
使用最小花费爬楼梯
要计算出达到楼顶的最低花费,先要求出 楼顶 - 1 或 楼顶 - 2 位置的最低花费
不同路径
需要到达星星位置,就要先到达 1/2 的位置,要达到 1/2 的位置,需要先达到 1/2 的各自得左边或上边,依次类推......
最大子数组和
以 i 位置为结尾的数组中和最大的子数组,与以 i - 1位置为结尾的数组中和最大的子数组也由一定的关系,但关系或许不是绝对的,需要分析
动态规划题目做题步骤
动态规划类题目做题步骤一般分为 5 步
- 状态表示
将需要的状态填入 dp 表中,这个状态一般是根据 题目要求 + 经验得出的。其中,线性 dp 表填 dp[i] 的经验为:以 i 位置为结尾, +(题意)或者 以 i 位置为开头,+ (题意)这里的题意,一般指题目中要求的东西。比如:使用最小花费爬楼梯问题中,dp[i] 就表示:爬到 i 位置时的最小花费;最大子数组和问题中,dp[i] 就表示以 i 位置为结尾的数组中最大的和
当然,dp 表也有可能是二维,甚至三维,具体需看题意,比如,不同路径中就需要 dp[i][j] 表示走到坐标为 [i, j] 位置时的路径数。
- 状态转移方程
状态转移方程就是填 dp 表的关键,通俗的来说就是 dp[i] 等于什么,通过距离 i 位置最近的一步,来划分问题,如通过 dp[i - 1]、dp[i + 1]、dp[i - 2] 等等,如果状态转移方程写不出来,就要思考状态表示的正确性了。
- 初始化
初始化 dp 数组,是为了防止填写 dp 表的时候发生越界。
- 确定填表顺序
有的 dp表是从坐往右依次填,有的是从右往左依次填,取决于定义 dp 表时的状态表示。
- 确定返回值
既然选择了使用动态规划解决这道问题,那么最终答案一定会直接或间接通过 dp 表产生!
动态规划题目解析
动态规划算法写代码的步骤比较固定:
- 创建 dp 表
- 初始化(保证填表的时候不越界)
- 填表顺序及填表,保证填当前状态的时候,所需要的状态已经计算过了
- 返回值
将 dp 表多开一列,一般是为了方便初始化,但多开一列后要注意原数组的下标需要与 dp 表有对应关系,再一个就是多开的那一列填的值必须保证 dp 表的填写正确!
泰波那契数模型
第 N 个泰波那契数
第 N 个泰波那契数

这道题是动态规划的基础,一定要好好理解这道题目!
class Solution {
public:
int tribonacci(int n) {
vector<int> dp(n + 1); // dp[i] 表示第 i 个泰波那契数列
if(n == 0) return 0;
if(n == 1|| n == 2) return 1;
dp[0] = 0, dp[1] = 1, dp[2] = 1;
// 由题意得:状态转移方程为 :dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
for(int i = 3; i <= n; i++)
{
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
}
return dp[n];
}
};三步问题
三步问题
 泰波那契数模型
泰波那契数模型
class Solution {
public:
int waysToStep(int n) {
const int MOD = 1e9 + 7;
vector<int> dp(n + 1);
// 初始化 dp 表,防止越界
if(n == 1) return 1;
if(n == 2) return 2;
if(n == 3) return 4;
dp[1] = 1, dp[2] = 2, dp[3] = 4;
for(int i = 4; i <= n; i++)
{
dp[i] = ((dp[i - 1] + dp[i - 2])%MOD + dp[i - 3])%MOD;
}
return dp[n];
}
};使用最小花费爬楼梯
使用最小花费爬楼梯

class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int n = cost.size();
vector<int> dp(n);
// dp[i] 表示以 i 位置为起点,到达楼顶的最小花费
dp[n - 1] = cost[n - 1], dp[n - 2] = cost[n - 2];
for(int i = n - 3; i >= 0; i--)
{
dp[i] = min(cost[i] + dp[i + 1], cost[i] + dp[i + 2]);
//可以从 i - 1 位置或者 i - 2 位置到达 i 位置,取其中花费最小的
}
return min(dp[0], dp[1]);
}
};路径问题
不同路径
不同路径

使用二维 dp 表解决,只需要处理好初始化即可!
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
dp[0][1] = 1; // 初始化,其余多开的地方全部为 0
for(int i = 1; i <= m; i++)
{
for(int j = 1; j <= n; j++)
{
// dp[i][j] 表示走到走到 i 行 j 列为结尾的路径总数(加上一行一列的情况下)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m][n];
}
};不同路径 Ⅱ
不同路径 II

这道题目相比于 不同路径 ,在方格中添加了障碍物,一但在路上遇到了障碍物,那么这条路就走不通了,这个 i,j 位置的 dp表的值就要置 0,并且 i, j 位置的 dp 值会一直影响后面的 dp 值,最终影响最终结果!
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
dp[0][1] = 1;
for(int i = 1; i <= m; i++)
{
for(int j = 1; j <= n; j++)
{
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
if(obstacleGrid[i - 1][j - 1]) dp[i][j] = 0;
}
}
return dp[m][n];
}
};珠宝的最高价值
珠宝的最高价值
这道题目的思路其实也挺简单的,相对于普通的二维 dp 中加入了一次判断大小的过程。
class Solution {
public:
int jewelleryValue(vector<vector<int>>& frame) {
int m = frame.size();
int n = frame[0].size();
// dp[i][j]为加上扩展的数组,到达第第 i 行,第 j 列时的最大价值
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
for(int i = 1; i <= m; i++)
{
for(int j = 1; j <= n; j++)
{
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + frame[i - 1][j - 1];
}
}
return dp[m][n];
}
};下降最短路径和
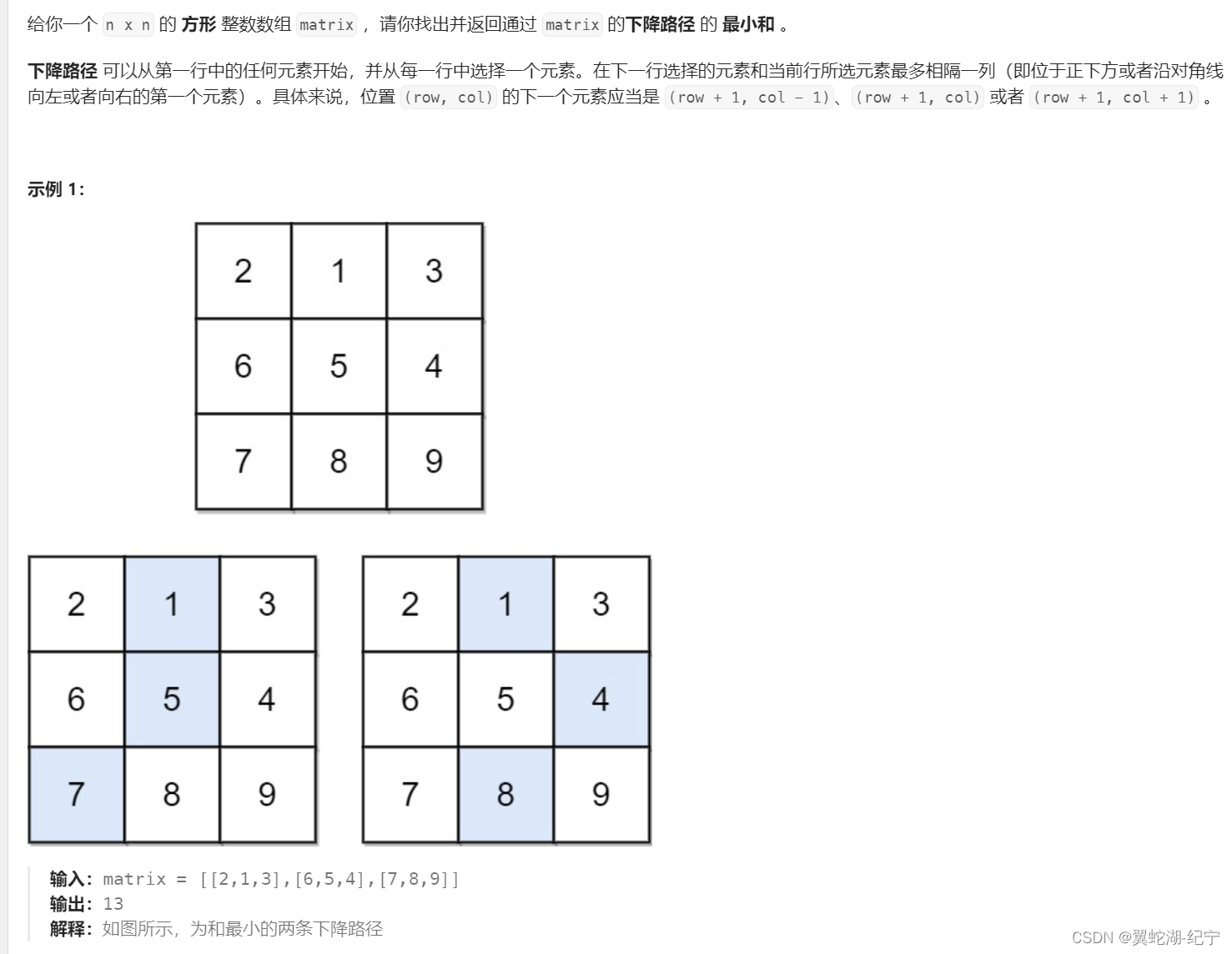
下降路径最小和
这道题就要认真对 dp 表多开的那一列做初始化了!但如果不多开一列的话,边界条件可能会更难处理。为了在状态转移方程中求最小值的时候不被多开的那一列干扰,可以初始化为 INT_MAX
class Solution {
public:
int minFallingPathSum(vector<vector<int>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 2));
for(int i = 1; i <= m; i++) dp[i][0] = INT_MAX; // 初始化
for(int i = 1; i <= m; i++) dp[i][n + 1] = INT_MAX;
for(int i = 1; i <= m; i++)
{
for(int j = 1; j <= n; j++)
{
dp[i][j] = min(dp[i - 1][j], min(dp[i - 1][j - 1], dp[i - 1][j + 1])) + matrix[i - 1][j - 1];
}
}
int min_path = INT_MAX;
for(int j = 1; j <= n; j++)
{
if(dp[m][j] < min_path) min_path = dp[m][j];
}
return min_path;
}
};地下城游戏
地下城游戏
这道题就采用了以 i,j 位置为起点的做法,这种做法比较方便计算。当然也可以使用以 i,j 位置为终点的 dp 思路,但需要开两个 dp 表,而且处理起来比较的复杂,不推荐。 地下城游戏
地下城游戏
class Solution {
public:
int calculateMinimumHP(vector<vector<int>>& dungeon){
int m = dungeon.size();
int n = dungeon[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
// dp[i][j] 表示从 [i,j] 位置过后,到达终点所需要的最小健康点数
for(int i = 0; i <= m; i++) dp[i][n] = INT_MAX;
for(int j = 0; j <= n; j++) dp[m][j] = INT_MAX;
dp[m][n -1] = dp[m - 1][n] = 1; // 保证计算出 i, j 位置救到公主的时候,起码要有 1 滴血
for(int i = m -1; i >= 0; i--)
{
for(int j = n - 1; j >= 0; j--)
{
dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];
dp[i][j] = max(1, dp[i][j]);
// 如果 dp[i][j] 计算下来小于 0 ,说明后面有大血包,以至于在当前位置血量为负都行,但这是不符合游戏规则的
// 所以到 i,j 位置时,起码得有 1 健康值
}
}
return dp[0][0];
}
};简单多状态问题
多状态问题,即 dp[i] 位置的状态,可能不只有一种,可能有多种情况,这些情况都要考虑进去!
按摩师
按摩师

dp[i] 的状态表示,填写都需要经过多方面思考。
class Solution {
public:
int massage(vector<int>& nums) {
int n = nums.size();
if(n == 0) return 0;
vector<int> dpf(n), dpg(n);
// dpf[i] 表示选择到 i 位置的时候,这个值 选, 得到的最大时长
// dpg[i] 表示选择到 i 位置的时候,这个值不选,得到的最大时长
dpf[0] = nums[0], dpg[0] = 0;
for(int i = 1; i < n; i++)
{
dpf[i] = dpg[i - 1] + nums[i];
dpg[i] = max(dpf[i - 1], dpg[i - 1]);
// dpg[i] i 位置不选, i - 1 位置也可能不选也可能选 ,看哪个值最大就选哪个
}
return max(dpf[n - 1], dpg[n - 1]);
}
};打家劫舍 Ⅱ
打家劫舍 II

这道题的多种状态为:小偷是否偷第一间房,如果他偷了第一间,那就不能偷第二间,最后一间,所以只需要在 [3, n - 1] 之间找出最高金额,再加上第一间的金额即可;如果他没有偷第一间,那就是再 [2,n] 之间找出最高金额,最后再找出求出的这两个最高金额中最大的那个即可。
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
// 两种状态计算的方式相同,找出最大的那个即可!
return max(nums[0] + _rob(nums, 2, n - 2), _rob(nums, 1, n - 1));
}
int _rob(vector<int>& nums, int left, int right)
{
if(left > right) return 0;
int n = nums.size();
vector<int> f(n); // 表示偷的 dp 表
vector<int> g(n); // 表示不偷的 dp 表
f[left] = nums[left];
for(int i = left + 1; i <= right; i++)
{
// 两表之间需要相互计算,因此需要一起填表
f[i] = g[i - 1] + nums[i];
g[i] = max(f[i - 1], g[i - 1]);
}
return max(f[right], g[right]);
}
};
删除并获得点数
删除并获得点数
先排序,找出最大的数,并将所有的数映射到数组,再利用“打家劫舍”的多状态思路解决问题。
class Solution {
public:
int deleteAndEarn(vector<int>& nums) {
sort(nums.begin(), nums.end());
int n = *(nums.end() - 1); // 求出 nums 中最大的元素,方便开 arr 数组
vector<int> arr(n + 1, 0); // 相当于将点数相邻的计数并放在一起了
for(auto x: nums) arr[x] += x; // 将 x 的 '和' 全部映射在 arr 数组里
// 利用 “打家劫舍” 的思路, 求出能获得的最大点数
vector<int> f(n + 1); // 获得这个位置的点数,并不获得相邻位置的点数
vector<int> g(n + 1); // 不获得这个位置的点数
for(int i = 1; i <= n; i++)
{
f[i] = g[i - 1] + arr[i];
g[i] = max(g[i - 1], f[i - 1]);
}
return max(f[n], g[n]);
}
};粉刷房子
粉刷房子

以 i 位置为结尾的最小花费,当前位置的颜色只需要与前一个位置不同即可,在这个条件下求最小花费,i 位置可以有三个颜色,因此有三种状态需要考虑,他们都可能出现不同的结果,最终选择最小的那个。
class Solution {
public:
int minCost(vector<vector<int>>& costs) {
int m = costs.size();
int n = costs[0].size();
// dp[i] 表示刷到第 i 个房子时的最小花费
// 但dp[i] 又可以继续细分为 多种状态
vector<vector<int>> dp(m + 1, vector<int>(n));
for(int i = 1; i <= m; i++)
{
dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i - 1][0]; // i 位置为 红
dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i - 1][1]; // i 位置为 蓝
dp[i][2] = min(dp[i - 1][0], dp[i - 1][1]) + costs[i - 1][2]; // i 位置为 绿
}
return min(dp[m][0], dp[m][1], dp[m][2]);
}
};复杂多状态问题
买卖股票的最佳时机含冷冻期
买卖股票的最佳时机含冷冻期
如果子状态比较多且相互影响难以分析,可以画状态转移图,必须搞清楚状态之间的关系!

class Solution {
public:
int maxProfit(vector<int>& prices) {
// dp[i] 表示第 i 天时,你的最大利润
// dp[i] 可以细分 为三种
//dp[i][0] 表示第 i 天结束时处于买入状态,dp[i][1] 第 i 天结束处于可交易状态,dp[i][2] 第 i 天结束处于冷冻期状态
int m = prices.size();
if(m == 1) return 0;
vector<vector<int>> dp(m + 1, vector<int>(3));
dp[0][0] -= prices[0];
for(int i = 1; i <= m; i++)
{
// 如果子状态关系不好分析, 可以画状态转移表
// 状态之间又关系且可能互相影响
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i - 1]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]);
dp[i][2] = dp[i - 1][0] + prices[i - 1];
cout << dp[i][0] << " " << dp[i][1] << " " << dp[i][2] << endl;
}
return max(dp[m][1], dp[m][2]);
}
};买卖股票的最佳时机含手续费
买卖股票的最佳时机含手续费

class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
// dp[i] 表示第 i 天结束时,获得的最大利润
int m = prices.size();
vector<vector<int>> dp(m + 1, vector<int>(2, 0));
// 0 代表第 i 天结束后,处于买入状态,1 代表卖出状态
dp[0][0] -= prices[0];
for(int i = 1; i <= m; i++)
{
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i - 1]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i - 1] - fee);
}
return dp[m][1];
}
};买卖股票的最佳时机 Ⅲ
买卖股票的最佳时机 III

用循环限制交易次数即可!
class Solution {
public:
const int INF = 0x3f3f3f3f; // 初始化第一行, 为了后续求 max 的时候,不影响后续的结果!
int maxProfit(vector<int>& prices) {
int m = prices.size();
// dp[i] 表示在第 i 天结束时获得的最大利润
// dp[i] 可以分为好几个状态
vector<vector<int>> f(m, vector<int>(3, -INF)); // 买入状态
vector<vector<int>> g(m , vector<int>(3, -INF)); // 卖出状态
f[0][0] = -prices[0], g[0][0] = 0;
for(int i = 1; i < m; i++)
{
for(int j = 0; j < 3; j++)
// j 表示参与交易的次数
{
f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);
g[i][j] = g[i - 1][j];
if(j - 1 >= 0) g[i][j] = max(g[i - 1][j], f[i - 1][j - 1] + prices[i]);
}
}
int ret = 0;
for(int j = 0; j < 3; j++) ret = max(ret, g[m - 1][j]);
return ret;
}
};买卖股票的最佳时机 Ⅳ
买卖股票的最佳时机 IV
与限制次数为 2 次是相同的做法,用循环 k 次保证所有交易次数和状态能得到结果。
class Solution {
public:
const int INF = 0x3f3f3f3f; // 初始化第一行, 为了后续求 max 的时候,不影响后续的结果!
int maxProfit(int k, vector<int>& prices) {
int m = prices.size();
k = min(k, m / 2);
// dp[i] 表示在第 i 天结束时获得的最大利润
// dp[i] 可以分为好几个状态
vector<vector<int>> f(m, vector<int>(k + 1, -INF)); // 买入状态
vector<vector<int>> g(m , vector<int>(k + 1, -INF)); // 卖出状态
f[0][0] = -prices[0], g[0][0] = 0;
for(int i = 1; i < m; i++)
{
for(int j = 0; j <= k; j++) // 为什么要用 k 来循环,保证一共交易 j 次, 每次都有对应的最大利润
{
f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);
g[i][j] = g[i - 1][j];
if(j - 1 >= 0) g[i][j] = max(g[i - 1][j], f[i - 1][j - 1] + prices[i]);
}
}
int ret = 0;
for(int j = 0; j <= k; j++) ret = max(ret, g[m - 1][j]);
return ret;
}
};子数组问题
最大子数组和
最大子数组和
class Solution {
public:
int maxSubArray(vector<int>& nums) {
// dp[i]:以 i 位置为结尾的数组的最大子数组和
int n = nums.size();
vector<int> dp(n + 1);
dp[0] = 0;
for(int i = 1; i <= n; i++)
{
dp[i] = max(nums[i - 1], dp[i - 1] + nums[i - 1]);
}
// 不一定以 n - 1 位置为结尾时,子数组的和最大
int ret = dp[1];
for(int i = 1; i <= n; i++) if(dp[i] > ret) ret = dp[i];
return ret;
}
};环形子数组的最大和
环形子数组的最大和
将结果分为两种,一种是不包含头尾的状态,一种是包含头尾的状态,包含头尾就需要使用正难则反的思想,将问题变为数组内进行操作!
class Solution {
public:
int maxSubarraySumCircular(vector<int>& nums) {
const int INF = 0x3f3f3f3f;
int n = nums.size();
// 环形 dp 问题, 转化为非环形
// 1. 目标子数组未连接头尾,直接求最大连续子数组的和
// 2. 目标子数组连接头尾,最大连续子数组的和 转化为用整个数组的和 sum 减去 最小连续子数组的和!
// dp[i] 表示以 i 位置为结尾的子数组和的最大值, sp[i] 表示以 i 位置为结尾的子数组和的最小值
vector<int> dp(n + 1);
auto sp = dp; // 和的最小值
dp[0] = -INF, sp[0] = INF;
int sum = 0;
for(int i = 1; i <= n; i++)
{
dp[i] = max(dp[i - 1] + nums[i - 1], nums[i - 1]);
sp[i] = min(sp[i - 1] + nums[i - 1], nums[i - 1]);
sum += nums[i - 1];
}
int max_dp = dp[1];
int min_sp = sp[1];
for(int i = 1; i <= n; i++)
{
if(dp[i] > max_dp) max_dp = dp[i];
if(sp[i] < min_sp) min_sp = sp[i];
}
// 当数组全部为负数的时候, sum 等于 sp[i],这种情况直接返回 max_dp
return dp[i] == sum ? max_dp : max(max_dp, sum - min_sp);
}
};乘积最大数组
乘积最大子数组
class Solution {
public:
int maxProduct(vector<int>& nums) {
int n = nums.size();
// 因为两个负数乘起来是一个正数,因此不能直接用 nums[i] * dp[i - 1]
// 因此, 当 nums[i] 等于一个负数的时候, 需要乘一个最小乘积,才能得到最大的数
// 所以, 还需要一个数组来记录前乘积最小的数组
vector<int> f(n + 1);
auto g = f;
f[0] = 1, g[0] = 1;
for(int i = 1; i <= n; i++)
{
// 需要判断 nums[i] 的正负
if(nums[i - 1] > 0)
{
f[i] = max(f[i - 1] * nums[i - 1], nums[i - 1]);
g[i] = min(g[i - 1] * nums[i - 1], nums[i - 1]);
}
else
{
f[i] = max(g[i - 1] * nums[i -1], nums[i - 1]);
g[i] = min(f[i - 1] * nums[i - 1], nums[i - 1]);
}
}
int ret = f[1];
for(int i = 1; i <= n; i++) if(f[i] > ret) ret = f[i];
return ret;
}
};