【格与代数系统】格与代数系统汇总

目录

常见的偏序关系 

覆盖

哈斯图

例1

例2

例3

 格与哈斯图

例1

例2

---

常见的偏序关系 

偏序关系：自反性+反对称性+传递性

整数集合上的小于等于（大于等于）关系、幂集中的包含关系 、正整数的整除和整倍数关系都满足偏序关系，是一些常见的偏序关系

一个偏序关系的逆关系也是偏序关系

覆盖

设是一个偏序集，如果对任何, 满足且, 同时不存在其他的元素z∈A, 能够让且成立，即，则称元素y覆盖x。

覆盖：“直接”+“偏序”

例：{8，4，2，1}的小于等于关系中，8覆盖4，但是8不覆盖2。

哈斯图

哈斯图是一种用来表示偏序关系的图。

在哈斯图中，用小圈来表示元素。如果存在, 满足且, 则把x画在y下方。如果y覆盖x，则在x和y中间连线，线的方向默认从下往上。

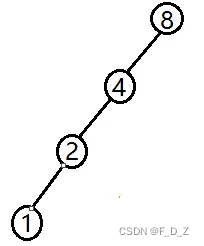
例1

{8, 4, 2, 1}的小于等于关系中，哈斯图表示为：

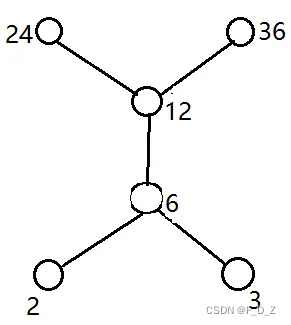
例2

{36,24,12,6,3,2}的整除关系中，哈斯图表示为：

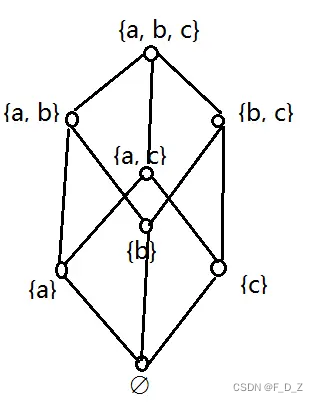
例3

 设，幂集 ，则的哈斯图：

格与哈斯图

格：偏序集+上下确界

哈斯图可以用于判断和刻画格

判断是否是格：任意两个元素，是否都有上下确界

例1

 其中，任意两个元素, 都有上下确界, 所以是格。

例2

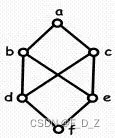
其中，选取两个元素b、c, 它们所有的下界: d、e、f，但是d和e没有可比性 ，故b、c不存在下确界（最大下界），所以上例不是格。