redis源码分析

news2024/10/5 14:33:32

是什么

是基于内存(而不是磁盘)的kv(而不是关系型mysql那种)数据库，通过空间换时间

源码分析

跳表skiplist

假设你有个有序链表，你想看某个特定的值是否出现在这个链表中，那你是不是只能遍历一次链表才能知道，时间复杂度为O(n)。
在这里插入图片描述

可能有人会问为什么不直接用连续存储，我们还能用二分查找，用链表是想继续保留它修改时间复杂度低的优势。那我们如何优化单次查找的速度？其实思路很像是二分查找，但单链表无法随机访问的特性限制了我们，但二分逐渐缩小范围的思路启发了我们，能不能想什么办法逐渐缩小范围？

我是不是可以在原链表之上新建一个链表，新链表是原链表每隔一个节点取一个。假设原链表为L0，新链表为L1，L1中的元素是L0中的第1、3、5、7、9……个节点，然后再建立L1和L0中各个节点的指针。这样L1就可以将L0中的范围缩小一半，同理对L1再建立新链表L2……，更高level的链表划分更大的区间，确定值域的大区间后，逐级向下缩小范围，如下图。
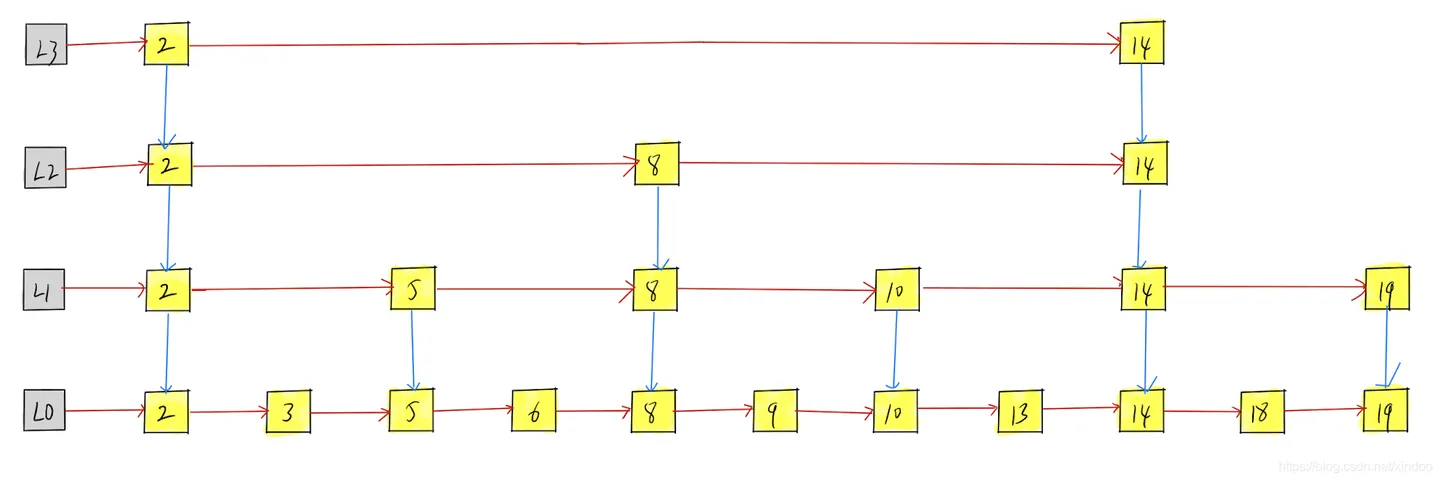在这里插入图片描述假设我们想找13，我们可以在先在L3中确定2-14的范围，然后在L2中确定8-14的范围，接着在L1中确定10-14的范围，最后在L0中找到13，整体寻找路径如下图红色路径，是不是比直接在L0中找13的绿色路径所经过的节点数少一些
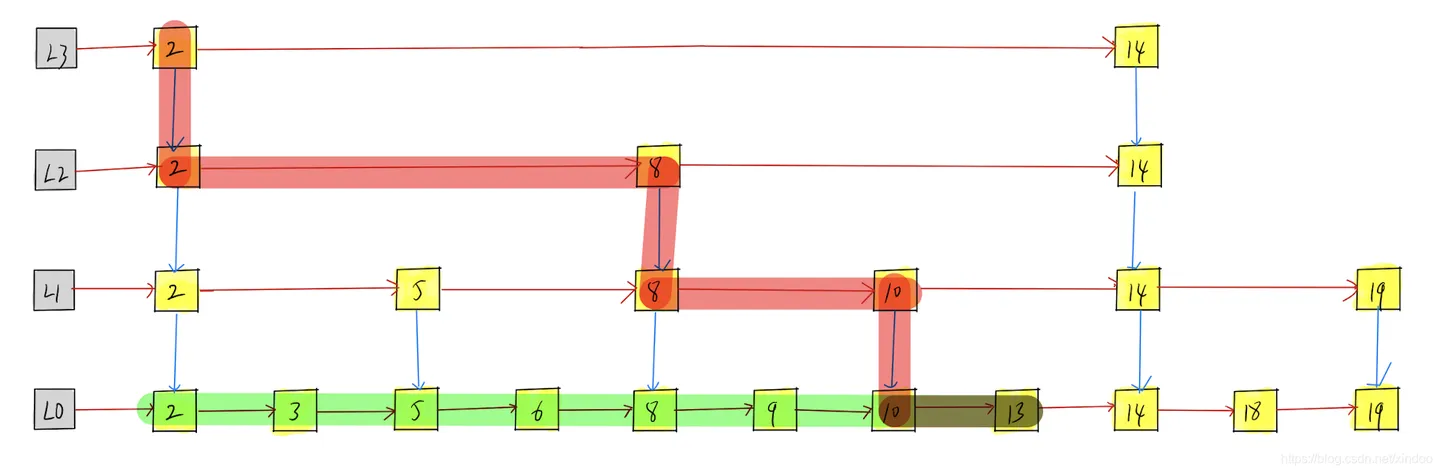
在这里插入图片描述
其实这种实现很像二分查找，只不过事先将二分查找的中间点存储下来了，用额外的空间换取了时间，很容易想到其时间复杂度和二分查找一致，都是O(logn)。

如果链表中插入或者删除了某个节点怎么办？，是不是每次数据变动都要重建整个数据结构？

其实不必，我们不需要严格保证两两层级之间的二分之一的关系，只需要概率上为二分之一就行，删除一个节点好说，直接把该节点所在的每个层级中的对应节点删掉，插入节点时，新节点以指数递减的概率往上层链表插入即可。 比如L0中100%插入，L1中以1/2的概率插入，如果L1中插入了，L2中又以1/2的概率插入…… 注意，只要高Level中有的节点，低Level中一定有，但高Level链表中出现的概率会随着level指数即1/2的n次方递减，最终跳表可能会长这个样子。
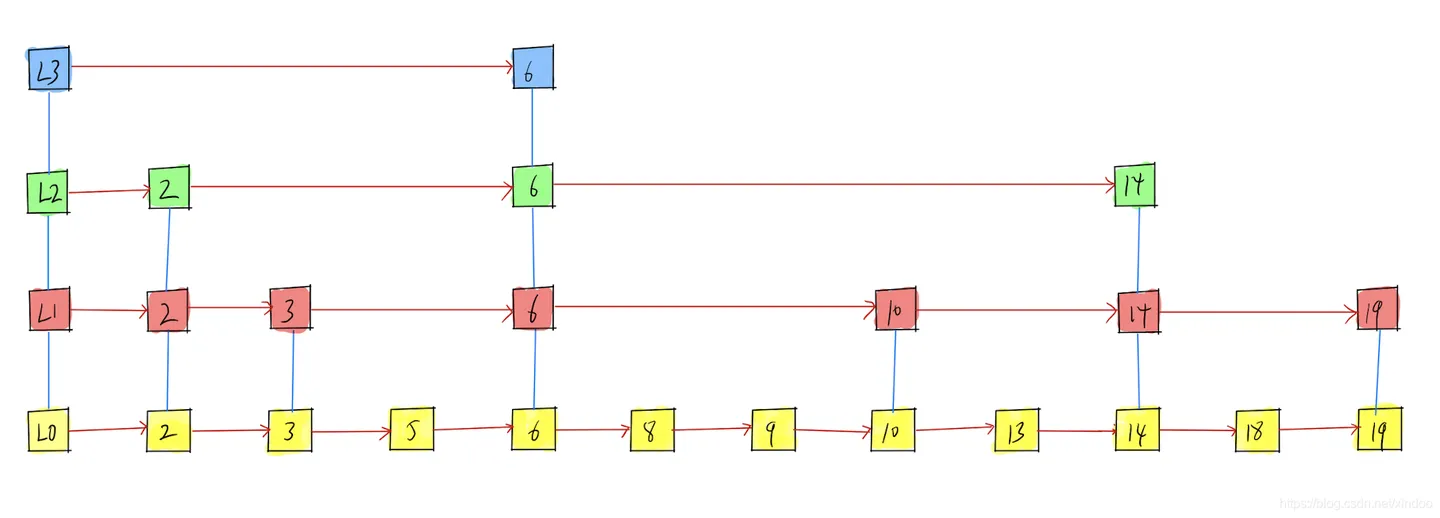
在这里插入图片描述

redis跳表数据结构

Redis中的有序集合(sorted set)的相关操作(比如zadd、zrange)，其底层实现就是skiplist。我们接下来看下redis是如何实现skiplist的。

typedef struct zskiplist {
    struct zskiplistNode *header, *tail; // 头尾节点指针 
    unsigned long length;   // 最底层节点个数  
    int level;  // 最高多少级链表(最大层数，redis默认设置为32即ZSKIPLIST_MAXLEVEL，最底层可容纳2的32次方个节点) 
} zskiplist;

我们先来看下redis中zskiplist的定义，没啥内容，就头尾指针、长度和级数，重点还是在zskiplistNode中。zskiplistNode中是有前向指针的，每个节点都有pre指针即下面的backward属性索引前一个节点，所以跳表还是个双向链表

typedef struct zskiplistNode {
    sds ele;   // 节点存储的具体值 
    double score;   // 节点对应的权值 
    struct zskiplistNode *backward; // 当前节点的前一个节点的地址(由此可知跳表以双向链表为基础，但也只在最底层是双向)
    struct zskiplistLevel {
        struct zskiplistNode *forward; // 当前节点在当前层的后向指针即下一个节点的地址 
        unsigned long span;  // 当前节点当前层到下一个节点的跨度(以最底层作为基准相隔多少个节点) ，就是数箭头数，每一层最后一个节点的span就是该节点到(最底层)最后一个节点的距离即箭头数那你
    } level[];//多层
} zskiplistNode;

redis中的skiplist实现稍微和我们上文中讲的不大一样，它并不是简单的多级链表的形式，而是直接在zskiplistNode中的level[]将不同level的节点的关联关系组织起来，zskiplist的结构可视化如下。
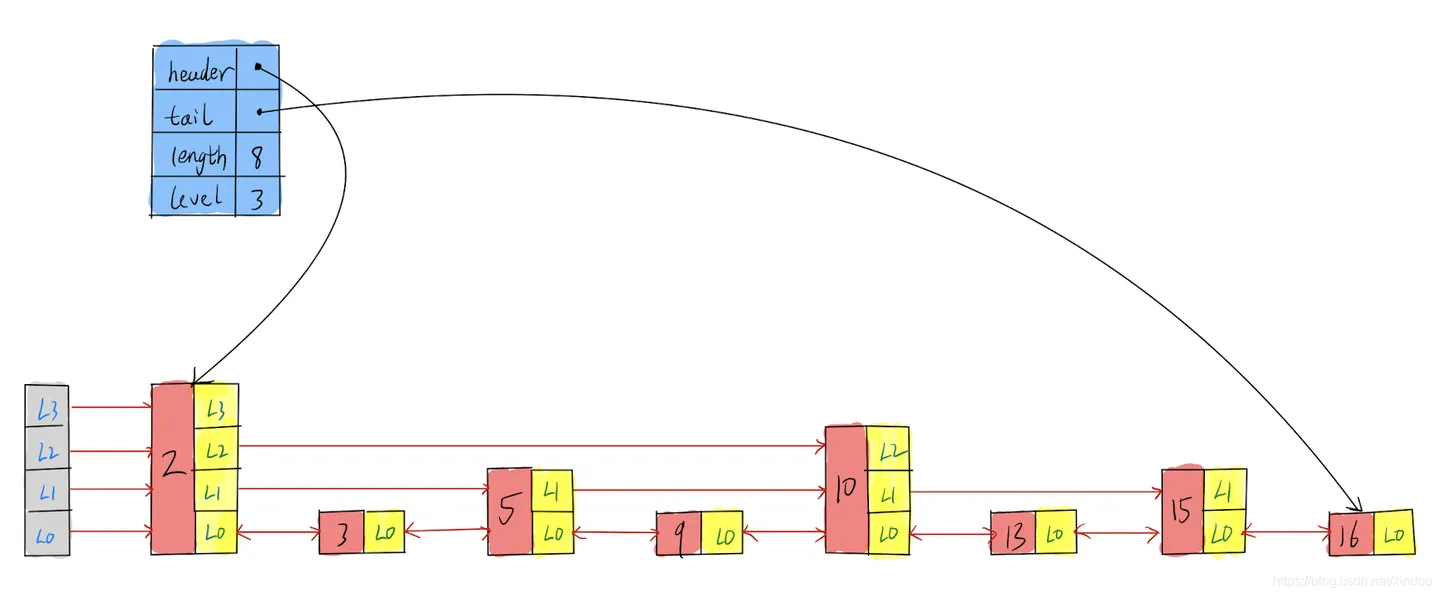
在这里插入图片描述

redis跳表操作

创建跳表
/* 创建跳表 */
zskiplist *zslCreate(void) {
    zskiplist *zsl;
    zsl = zmalloc(sizeof(*zsl));
    zsl->level = 1;
    zsl->length = 0;
    zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);  // 创建含有32层的头节点
    for (int j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
        zsl->header->level[j].forward = NULL;
        zsl->header->level[j].span = 0;
    }
    zsl->header->backward = NULL;
    zsl->tail = NULL;
    return zsl;
}
插入节点
/* 在跳表中插入一个新的节点, */
zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    unsigned int rank[ZSKIPLIST_MAXLEVEL];
    int i, level;

    serverAssert(!isnan(score));
    x = zsl->header;
    /*这个函数从当前最高层数开始将每一层刚好小于(大于的前一个)新节点score值的节点保存在update[]数组中，然后将该节点距离头节点的节点数(以L0为基准)保存在rank数组中，例如在level=3那层，权值10的节点和头节点之间的距离为5，如果这时新节点权值为11，那么在L3即rank[3]=5*/
    for (i = zsl->level-1; i >= 0; i--) {
        /*每一层的rank的值都是在上一层的基础上接着进行计算，
        因为一直向着权值变大的方向移动而没有后退，
        最高层初始化为0*/
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
        //在当前层与当前节点x的下一个节点比较，新权值更大则向后移动
        while (x->level[i].forward &&
                (x->level[i].forward->score < score ||
                    (x->level[i].forward->score == score &&
                    sdscmp(x->level[i].forward->ele,ele) < 0)))
        {
            rank[i] += x->level[i].span;
            x = x->level[i].forward;
        }
        update[i] = x;
        //第i层刚好小于新权值的节点
    }

    /* skiplist中不会出现重复的元素，但我们允许重复的分值，因为如果是调用zslInsert()的话，不会出现重复插入两个相同的元素，因为在zslInsert()中已经判断了hash表中是否存在*/
    level = zslRandomLevel();  // 生成一个随机值，确定最高需要插入到第几级链表里  


	/*如果超出当前记录的用到的最高层，说明新节点在该最高层之后到新最高层level中都是头节点后的第一个节点*/
    if (level > zsl->level) {
        for (i = zsl->level; i < level; i++) {
            /*刚好小于新节点的节点就是头节点，
            rank就是记录刚好小于新节点的节点到头节点的距离，
            头节点和头节点之间距离当然就是0*/
            rank[i] = 0;
            
            //刚好小于新节点的节点就是头节点
            update[i] = zsl->header;
            /*联系到后面的那句x->level[i].span = 
            update[i]->level[i].span - (rank[0] - rank[i])
            而rank[i]=0，update[i]->level[i].span = 
            zsl->length，即x->level[i].span =
            zsl->length - rank[0]，
            即二者共同使得新节点到头节点距离为*/
            update[i]->level[i].span = zsl->length;
        }
        zsl->level = level;
    }
    x = zslCreateNode(level,score,ele);  // 为插入的数据创建新节点  
    for (i = 0; i < level; i++) {
    	//将新节点插入到刚好小于之后刚好大于之前
        x->level[i].forward = update[i]->level[i].forward;
        update[i]->level[i].forward = x;

        /*新节点在第i层到下一个节点的距离*/
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
    }

    /* 为其他level增加span值，因为在原有俩节点之间插入了一个新节点 */
    for (i = level; i < zsl->level; i++) {
        update[i]->level[i].span++;
    }

    x->backward = (update[0] == zsl->header) ? NULL : update[0];
    if (x->level[0].forward)
        x->level[0].forward->backward = x;
    else
        zsl->tail = x;
    zsl->length++;
    return x;
}
int zslRandomLevel(void) {
    int level = 1;
    /*random返回随机32位uint，与运算相当于产生随机16位，
    ZSKIPLIST_P是1/4，那就是1/4概率为真，
    相当于每想多一层就要再乘1/4，
    效果就是每一层大致是其下一层节点数的1/4*/
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;//不能超过最大层数
}
更新节点

  • 正如上面跳跃表添加节点时所说，跳跃表上的节点数据有具有有序性的。所以更新表节点时也需要注意时候需要调整顺序，如果更新后的节点在跳跃表中的排位没有变化，则只需要更新节点上的score即可。如果更新后节点的排位发生改变，则需要先将原先的节点删除，然后新增一个score为新值的节点。

  • 下面这个函数就是根据value即sds ele和原score即curscore找到需要更新的节点并更新为新score即newscore

zskiplistNode *zslUpdateScore(zskiplist *zsl, double curscore, sds ele, double newscore) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    int i;

    //和查找一开始的动作一样
    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward &&
                (x->level[i].forward->score < curscore ||
                    (x->level[i].forward->score == curscore &&
                     sdscmp(x->level[i].forward->ele,ele) < 0)))
        {
            x = x->level[i].forward;
        }
        update[i] = x;
    }

    //如果curscore对应的节点时存在的，那么最底层下x->level[0].forward一定是指向curscore对应的节点，因为x->level[0]就是update[0]即最底层中刚好小于curscore的节点
    x = x->level[0].forward;
    //判断节点是否一致
    serverAssert(x && curscore == x->score && sdscmp(x->ele,ele) == 0);

    //如果更新节点的score后这个节点在跳跃表中的排位没有变化，那么就不需要进行复杂的删除节点添加节点的操作，只需要更新一下节点的score即可
    if ((x->backward == NULL || x->backward->score < newscore) &&
        (x->level[0].forward == NULL || x->level[0].forward->score > newscore))
    {
        x->score = newscore;
        return x;
    }

    //如果节点的排位发生改变，那么调用zslDeleteNode函数来删除跳跃表中的这个节点信息，比如各指针的关联，但不是释放内存
    zslDeleteNode(zsl, x, update);
    //重新添加score的值为newscore的节点
    zskiplistNode *newnode = zslInsert(zsl,newscore,x->ele);
    /* We reused the old node x->ele SDS string, free the node now
     * since zslInsert created a new one. */
    x->ele = NULL;
    //删除节点，释放内存
    zslFreeNode(x);
    return newnode;
}

跳表实例分析

查找

假设我们查找值为51的节点，查找步骤如下。
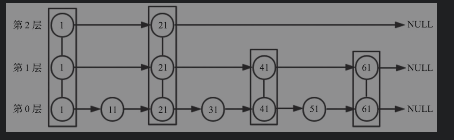
在这里插入图片描述

  1. 从第2层开始，1节点比51节点小，向后比较
  2. 21节点比51节点小，继续向后比较。第2层21节点的next指向null，所以下降一层
  3. 第1层中，21节点的next为41节点，继续向后比较。41节点的next为61节点，大于51节点，所以下降一层继续向后比较
  4. 第0层中，51节点为要查询的节点，返回结果

总结：通过将有序链表分层，由最上层依次向后查询，如果本层的当前节点的next节点刚好大于要找的值或指向null，则从当前节点开始，下降一层向后查找，依次类推，如果找到则返回节点，否则返回空。因此，在节点较多的时候可以跳过一些节点，查询效率大大提升，这就是跳跃表的基本思想。

插入

跳跃表插入节点的4个步骤

第一步：查找要插入的位置
  • 跳表如下图所示。长度为3，高度为2。若要插入节点31，高度为3。
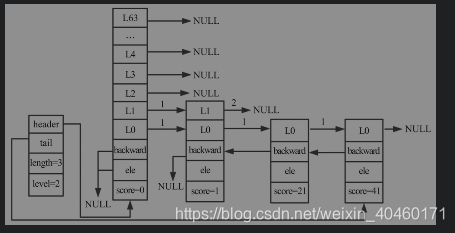
    在这里插入图片描述
  • 插入节点代码如下所示
x = zsl->header;
for (i = zsl->level - 1; i >= 0; i--) {
	rank[i] = i == (zsl->level - 1) ? 0 : rank[i + 1];
	while (x->level[i].forward && 
			(x->level[i].forward->score < score ||
				(x->level[i].forward->score == score &&
					sdscmp(x->level[i].forward->ele,ele) < 0)))
		{
			rank[i] += x->level[i].span;
			x = x->level[i].forward;
		}
		update[i] = x;
}
  • update[] : 插入节点时，需要更新被插入节点每层的前一个节点。由于每层更新的节点不同，所以需要将更新的节点记录在update[i]中。
  • rank[] : 记录当前层从header节点到update[i]节点所经历的步长，在更新update[i]的span和设置新插入节点的span时会用到。
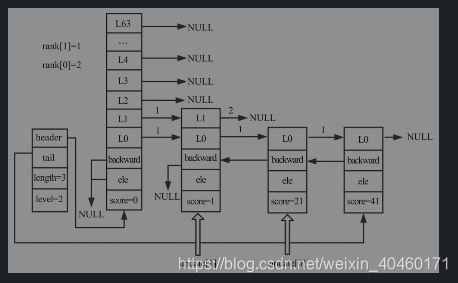
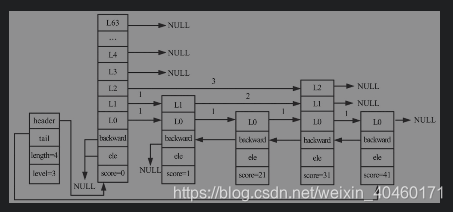
  • 查找节点（score=31, level = 3)的插入位置，逻辑如下：
  1. 第一次for循环，i = 1。 x为跳跃表的头节点。
  2. 此时i的值与zsl->level-1相等，所以rank[1]的值为0。
  3. header->level[1].forward存在，并且header->level[1].forward->score==1小于31，所以可以进入while循环，rank[1] = 1，x为第一个节点
  4. 第一个节点的第一层的forward指向null，所以不会再进入while。经过第一次for循环，rank[1]=1。x和update[1]都为第一个节点(score=1)。
  5. 经过第二次for循环，i=0。x为跳跃表的第一个节点(score=1)
  6. 此时i的值与zsl->level-1不相等，所以rank[0]等于rank[1]的值，值为1
  7. x->level[0]->forward存在，并且x->level[0].foreard->score==21小于31，所以进入while循环，rank[0]==2。x为第二个节点（score=21）
  8. x->level[0]->forward存在，并且x->level[0].foreard->score==41大于31，所以不会进入while，经过第二次循环，rank[0]=2。x和update[0]都为第二个节点（score=21)

update和rank复制后的跳跃表如下图所示。
在这里插入图片描述

第二步：调整跳跃表高度
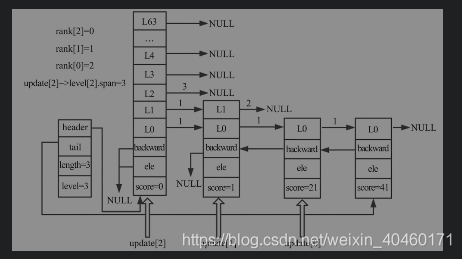
  • 由第一步可知插入节点高度为3，大于跳跃表高度2，因此需要调整跳表高度。
level = zslRandomLevel()；
for (i = zsl->level; i < level; i++ ) {
	rank[i] = 0;
	update[i] = zsl->header;
	update[i]->level[i].span = zsl->length;
} 
zsl->level = level;
  • 此时，i的值为2，level值为3，所以只能进入一次for循环。由于header的第0层到第1层的forward都已经指向相应的节点，而新添加的节点高度大于跳表的原高度，所以第2层只需要更新header节点即可。rank用来更新span的变量，其值是头节点到update[i]的节点数，此次修改的是头节点，所以rank[2]为0，update[2]一定为头节点。update[2]->level[2].span的值先赋值为跳跃表的总长度，后续在计算新插入节点level[2]的span时会用到此值。
  • 调整高度后跳表如下图所示

在这里插入图片描述

第三步：插入节点
  • 当update和rank都已赋值且节点都创建好后，便可以插入节点。
x = zslCreateNode(level, score, ele);
for (i = 0; i < level; i++) {
	x->level[i].forward = update[i]->level[i].forward;
	update[i]->level[i].forward = x;
	x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
	update[i]->level[i].span = (rank[0] - rank[i]) + 1;
}
  • level值为3，所以可以执行3次for循环，过程如下。
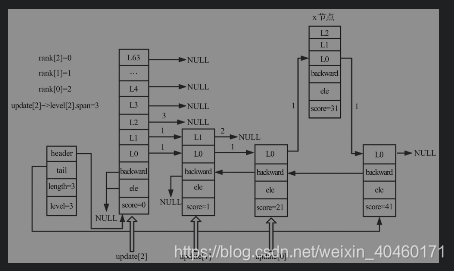
  1. 第一次for循环
    1.1 x的leve[0]的forward为update[0]的level[0]的forward节点，即x->level[0].forward为score=41的节点
    1.2 update[0]的level[0]的下一个节点为新插入的节点
    1.3 rank[0]-rank[0]=0,update[0]->level[0].span=1,所以x->level[0].span=1。
    1.4 update[0]->level[0].span = 0 + 1 = 1
  • 插入节点并更新0层后，跳表如下所示
    在这里插入图片描述
  1. 第2次for循环
    2.1 x的level[1]的forward为update[1]的level[1]的forward节点，即x->level[1].forward为null。
    2.2 update[1]的level[1]的下一个节点为新插入的节点
    2.3 rank[0]-rank[1] =1,update[1]->level[1].span=2,所以x->level[1].span=1
    2.4 update[1]->level[1].span=1+1=2
  • 插入节点并更新第1层后的跳表如下所示。
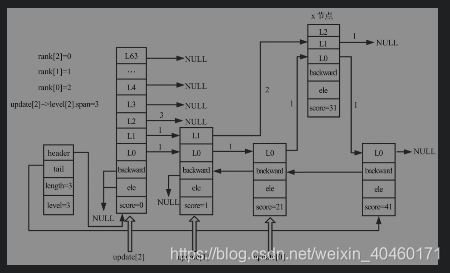
    在这里插入图片描述
  1. 第3次for循环
    3.1 x的level[2]的forward为update[2]的level[2]的forward节点，即x->level[2].forward为null。
    3.2 update[2]的level[2]的下一个节点为新插入的节点。
    3.3 rank[0]-rank[2]=2，因为update[2]->level[2].span=3，所以x->level[2].span=1
    3.4 update[2]->level[2].span=2+1=3
  • 插入节点并更新第2层后的跳表如下所示。
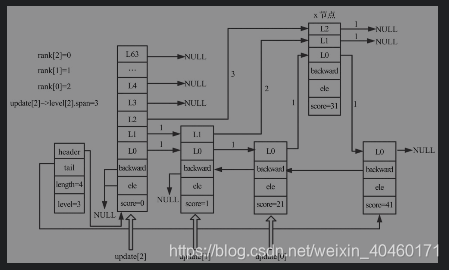
    在这里插入图片描述
第四步：调整backward
  • 根据update的赋值过程，新插入节点的前一个节点一定是update[0]，由于每个节点的后退指针只有一个，于此节点的层数无关，所以当插入节点不是最后一个节点时，需要更新被插入节点的backward指向update[0]。如果新插入节点是最后一个节点，则需要更新跳表的尾节点为插入新节点。插入节点后，更新跳表长度+1.
  • 插入新节点后的跳表如下所示。
    在这里插入图片描述

epoll多路复用IO机制

看这篇就够了

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1508173.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

JavaEE--SpringBoot配置⽂件

JavaEE--SpringBoot配置⽂件

配置文件的基本概念 properties的语法格式 读取配置文件的内容 properties的缺点 yml 主要使用yml yml的文件格式 先举一个例子&#xff0c;简单了解一下 验证结果如下&#xff1a; yml读取配置文件的内容 配置文件内容为空的时候的情况 配置内容为null时的情况 配置…
阅读更多...
算法项目（7）—— 文本检索图片

算法项目（7）—— 文本检索图片

本文包含什么？ 免环境配置,实现文本搜索图片全套代码以及代码介绍运行有问题? csdn上后台随时售后.项目说明 本文主要实现用文本搜索数据库中图片的功能. 项目运行 代码地址在文末 点击链接后选择T4的GPU: 将云盘中的代码文件clip_search.tar拖到下图位置上传代码: 执行…
阅读更多...
OD_2024_C卷_200分_9、园区参观路径【JAVA】【动态规划】

OD_2024_C卷_200分_9、园区参观路径【JAVA】【动态规划】

package odjava;import java.util.Scanner;public class 九_园区参观路径 {public static void main(String[] args) {Scanner sc new Scanner(System.in);int n sc.nextInt(); // 长 -> 行数int m sc.nextInt(); // 宽 -> 列数int[][] matrix new int[n][m]; // 地图…
阅读更多...
RK3568 xhci主控挂死问题

RK3568 xhci主控挂死问题

串口日志 rootjenet:~# [18694.115430] xhci-hcd xhci-hcd.1.auto: xHCI host not responding to stop endpoint command. [18694.125667] xhci-hcd xhci-hcd.1.auto: xHCI host controller not responding, assume dead [18694.125977] xhci-hcd xhci-hcd.1.auto: HC died; c…
阅读更多...
SQLiteC/C++接口简介

SQLiteC/C++接口简介

上一篇&#xff1a;SQLite——世界上部署最广泛的开源数据库&#xff08;简介&#xff09; 引言&#xff1a; 作为一种轻量级、嵌入式关系型数据库&#xff0c;SQLite已经成为许多应用和系统的首选解决方案。它是一个开源软件库&#xff0c;以小型、快速和易于使用而著称。为…
阅读更多...
利用yaml文件部署NacosXxl-job到阿里云的ACK

利用yaml文件部署NacosXxl-job到阿里云的ACK

背景介绍 随着容器化的技术成熟落地&#xff0c;拥抱各种成熟的容器化集群平台是加速我们落地的必然之路&#xff0c;目前国内以阿里云、华为云、腾讯云为平台的供应商为主&#xff0c;国外则以AWS&#xff0c;Azure为主&#xff0c;让我们借助平台已有的优势进行快速落地提高…
阅读更多...
zeta新增三个任务教程，即将刷新，速撸

zeta新增三个任务教程，即将刷新，速撸

这期是延续上期的教程&#xff0c;前面的任务不变&#xff0c;所以直接复制的前面的教程&#xff0c;多了三个任务更新在后面。 简单说一下&#xff0c;zeta是已经发币的公链项目&#xff0c;但是它社区还有6%的用户激励token份额没发完&#xff0c;做主网的几个简单任务可以获…
阅读更多...
文本向量评测MTEB和C-MTEB

文本向量评测MTEB和C-MTEB

文章目录 简介MTEBC-MTEB参考资料 简介 MTEB(Massive Text Embedding Benchmark)是目前评测文本向量很重要的一个参考&#xff0c;其榜单也是各大文本向量模型用来展示与其他向量模型强弱的一个竞技台。 C-MTEB则是专门针对中文文本向量的评测基准。 MTEB MTEB的目的是为了…
阅读更多...
基于51单片机超声波测距

基于51单片机超声波测距

目录 摘 要 2 ABSTRACT 3 目 录 4 1 绪论 1 1 概述 12 国内外发展现状 1 2 系统总体方案设计 21 设计要求 2 1&#xff09;可进行距离测量。 2 2&#xff09; 采用数码管显示距离数据。 2 3&#xff09; 可按键设置距离门限值 2 4&#xff09; 具有报警功能 22 方案选择 2 1 …
阅读更多...
华为手机的备忘录怎么传到苹果15手机上?

华为手机的备忘录怎么传到苹果15手机上?

曾经&#xff0c;我尝试过借助微信的复制粘贴功能&#xff0c;将备忘录内容一一传输。但这种方法既繁琐又容易出错&#xff0c;让我苦不堪言。我也曾试图通过数据线将数据导入电脑&#xff0c;再导入新手机。然而&#xff0c;这种方法不仅操作复杂&#xff0c;而且效率低下&…
阅读更多...
脱围：使用 ref 保存值及操作DOM

脱围：使用 ref 保存值及操作DOM

♻️ 前面多篇文章中提及&#xff1a;state 可以 ① 保存渲染间的数据&#xff1b; ② state setter 函数更新变量会触发 React 重新渲染组件。 // 子组件&#xff1a;显示当前时间 function Time() {return (<p>{new Date().toLocaleString()}</p>) }export def…
阅读更多...
伪分布HBase的安装与部署

伪分布HBase的安装与部署

1.实训目标 &#xff08;1&#xff09;熟悉掌握使用在Linux下安装伪分布式HBase。 &#xff08;2&#xff09;熟悉掌握使用在HBase伪分布式下使用自带Zookeeper。 2.实训环境 环境 版本 说明 Windows 10系统 64位 操作电脑配置 VMware 15 用于搭建所需虚拟机Linux系统 …
阅读更多...
蜂窝物联：智慧水产养殖解决方案

蜂窝物联：智慧水产养殖解决方案

一、系统介绍 集约化水产养殖水质在线监控系统是面向水产养殖集约、高产、高效、生态、安全的发展需求&#xff0c;基于智能传感、无线传感网、通信、智能处理与智能控制等物联网技术开发的&#xff0c;集水质环境参数在线采集、无线传输、智能处理、预警信息发布、决策支持、远…
阅读更多...
鸿蒙Harmony应用开发—ArkTS声明式开发（基础手势：Navigation）

鸿蒙Harmony应用开发—ArkTS声明式开发（基础手势：Navigation）

Navigation组件是路由导航的根视图容器&#xff0c;一般作为Page页面的根容器使用&#xff0c;其内部默认包含了标题栏、内容区和工具栏&#xff0c;其中内容区默认首页显示导航内容&#xff08;Navigation的子组件&#xff09;或非首页显示&#xff08;NavDestination的子组件…
阅读更多...
[虚拟机]

[虚拟机]

如果你电脑的物理机器硬件强大, 由于一台物理机器只能运行一个操作系统, 那么就会造成物理机器硬件的浪费 虚拟机:使用虚拟化技术&#xff0c;将一台物理机器虑拟化为多台虚拟机器&#xff08;Virtual Machine, VM)&#xff0c;每个虚拟机器都可以独立运行一个操作系统 虚拟机…
阅读更多...
一次直播和图像识别技术应用的探索之旅

一次直播和图像识别技术应用的探索之旅

背景 Think Better 很多行业都在“卷”&#xff0c;作为金融科技行业的信也&#xff0c;也不例外。除了卷云计算、大数据和人工智能这些非常有深度的技术以外&#xff0c;信也向着技术融合创新的方向逐步探索&#xff0c;做得更好一些&#xff0c;为用户提供更好的价值&#xf…
阅读更多...
【“双碳”目标】Acrel-2000Z分布式光伏发电监测系统解决方案

【“双碳”目标】Acrel-2000Z分布式光伏发电监测系统解决方案

1 概述 “十四五”期间&#xff0c;随着“双碳”目标提出及逐步落实&#xff0c;本就呈现出较好发展势头的分布式光伏发展有望大幅提速。就“十四五”光伏发展规划&#xff0c;国家发改委能源研究所可再生能源发展中心副主任陶冶表示&#xff0c;“双碳”目标意味着国家产业结…
阅读更多...
Django高级之-cookie-session-token

Django高级之-cookie-session-token

Django高级之-cookie-session-token 发展史 1、很久很久以前&#xff0c;Web 基本上就是文档的浏览而已&#xff0c; 既然是浏览&#xff0c;作为服务器&#xff0c; 不需要记录谁在某一段时间里都浏览了什么文档&#xff0c;每次请求都是一个新的HTTP协议&#xff0c; 就是请…
阅读更多...
20240306数据库的毫秒级上锁特性与可重复读级别的MVCC快照处理方式

20240306数据库的毫秒级上锁特性与可重复读级别的MVCC快照处理方式

从后端程序发送SELECT指令到数据库加上读锁&#xff0c;这个过程的时间差取决于多个因素&#xff0c;包括网络延迟&#xff08;如果存在&#xff09;、数据库服务器的处理能力、当前数据库的负载以及查询本身的复杂度。在你的情况下&#xff0c;由于后端程序和数据库服务器运行…
阅读更多...
Intel@cpu产品参数和命名@单核睿频和全核睿频

Intel@cpu产品参数和命名@单核睿频和全核睿频

文章目录 选择合适的cpuintel cpu型号和命名小结 cpu排行时钟速度睿频单核睿频和全核睿频网络上流传的方法 在线查询 产品比较跑分比较 选择合适的cpu 如何选择游戏 CPU - 英特尔 (intel.cn)在决定购买具体的产品之前,建议广泛地查阅用户对它的评价以及是否有哪些因素是不满足…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023