leetcode刷题(3):双指针和哈希表的使用

文章目录

- 1. 两数之和
- - 解题思路
  - c++实现
- 15. 三数之和
- - 解题思路
  - c++实现
- 11. 盛最多水的容器
- - 解题思路
  - c++实现
- 7. 整数反转
- - 解题思路
  - c++ 实现
- 34. 在排序数组中查找元素的第一个和最后一个位置
- - 思路
  - c++实现
- 704. 二分查找
- - 解题思路
  - c++ 实现
- 35.搜索插入位置
- - 解题思路
  - c++实现
- 153. 寻找旋转排序数组中的最小值
- - 解题思路
  - c++实现
- 88. 合并两个有序数组
- - 解题思路
  - c++ 实现
- 240. 搜索二维矩阵 II
- - 解题思路
  - c++实现
- 189.轮转数组
- - 解题思路
  - c++ 实现
- 74. 搜索二维矩阵
- 986. 区间列表的交集
- - 解题思路
  - c++实现

1. 两数之和

题目: 给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出和为目标值 target 的那两个整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例:
在这里插入图片描述

解题思路

使用hasmap来求解
hasmap的键key保存nums中的值，value保存nums中的值对应的索引
利用find或者count函数，来判断键值key是否存在(count()>0或者find()! = hasmap.end()则存在)

c++实现

解题1

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        vector<int> res;
        if (nums.size()==0) return res;

        unordered_map<int,int> map1;
   
        for(int i=0;i<nums.size();i++)
        {
            
            if(map1.count(target -nums[i])>0) 
            {
                res ={i,map1[target -nums[i]]};
            }
            else
            {
                 map1[nums[i]] = i;
            }
        }
        return res;
    }
};

在这里插入图片描述

解题2

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> hamap;
        int x = -1;
        for (int i = 0; i < nums.size(); i++)
        {
            x = target - nums[i];
            if (hamap.find(x) != hamap.end())
            {
                return{ hamap.find(x)->second, i };
            }
            hamap[nums[i]] = i;
        }
        return {};
    }
};

在这里插入图片描述

15. 三数之和

题目:给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例:
在这里插入图片描述

解题思路

使用双指针求解
双指针针对的是有序数组，因此需要先利用sort排序
由于要计算3个数之和，所以nums的size小于3则终止执行
如果排序后，最小的数>0 或者最大数小于0，则直接返回结果
遍历nums, 设置 left = i+1, right =len-1;
由于返回的结果不能包含重复3元组，因此当3个元素和为0时，左右指针需要跳过重复的值；
如果三数之和小于target 0时，则 left 加1向右移动，使得结果变大，使结果变小，靠近目标值0；
如果三叔之和小于0, 则right -1向左移动，使结果变小，靠近目标值0
注意最内侧的while 要加上left <right条件

c++实现

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> res;
        int len= nums.size();
        sort(nums.begin(),nums.end());
        if (len<3) return res;
        if(nums[0] >0 || nums[len-1]<0 ) return res;

        for(int i=0;i<nums.size();i++)
        {
            if (nums[i]>0) return res;
            int left =i+1,right =len-1;
            if(i>0 && nums[i] == nums[i-1]) continue;

            while(left < right)
            {
                if(nums[i]+nums[left]+nums[right] ==0)
                {
                    res.push_back({nums[i],nums[left],nums[right]});
                    while(left<right && nums[left] == nums[left+1]) left++;
                    while(left<right && nums[right] == nums[right-1]) right--;

                    left++;
                    right--;
                }
                else if (nums[i]+nums[left]+nums[right] <0) left++;
                else right--;
            }
    
        }
        return res;
    }
};

11. 盛最多水的容器

题目：给定一个长度为 n 的整数数组height。有 n 条垂线，第 i 条线的两个端点是(i, 0)和(i, height[i])。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例：
在这里插入图片描述

解题思路

使用双指针
注意！我们每次只要移动高度小的一边，因为移动小的那一边可能会增大，但是移动大的一边一定会减小

c++实现

class Solution {
public:
    int maxArea(vector<int>& height) {
        int res;
        int len = height.size();
        int left =0;
        int right = len-1;

        if (len<2) return res;

        while(left < right)
        {
            if (height[left] <= height[right])
            {
                 res = max(res,(right-left)*height[left]);
                 left++;
            }
            else
            {
                 res = max(res,(right-left)*height[right]);
                 right--;
            }
           
        }

        return res;
    }
};

在这里插入图片描述

7. 整数反转

题目：给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果。

如果反转后整数超过 32 位的有符号整数的范围 $2^{31}, 2^{31} − 1]$ ，就返回 0。

示例：
在这里插入图片描述

解题思路

如果为负数，将负数转化为正数，然后倒序，最后添加负号
%10 结果为个位数字, /10：除个位数字外的数值

c++ 实现

class Solution {
public:
    int reverse(int x) {
            bool flag = false;
            if (x<0) 
            {
                x=abs(x);
                flag =true;
            }
            
            long n=0;
            while(x!=0)
            {
                n =n*10 + x%10;
                x = x/10;
            }
            if(flag) n=n*(-1);

            return n> INT_MAX || n <INT_MIN ?0 :n;
        }
    
};

在这里插入图片描述

34. 在排序数组中查找元素的第一个和最后一个位置

题目：给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例：
在这里插入图片描述

思路

二分查找

c++实现

解法1：二分查找实现

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size()-1;
        int start = -1;
        int end = -1;
        while(left <= right)
        {
            int mid = (left + right) / 2;
            if(nums[mid] == target)
            {
                start = mid;
                end = mid;
                while(start>0 && nums[start-1] == target) start--; //寻找左边界
                while(end<nums.size()-1 && nums[end+1] == target) end++; //寻找右边界
                break;
            }
            else if(nums[mid] < target) left = mid + 1;
            else right = mid - 1;
        }
        return {start,end};
    }
};

在这里插入图片描述

解法2：双指针

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int L=0;
        int R=nums.size()-1;
        while(L<=R){
            if(nums[L]!=target) L++;
            if(nums[R]!=target) R--;
            if(L>=0&&R<nums.size() && 
                nums[L]==nums[R]&&nums[L]==target) break;
        }
        vector<int> ans;
        if(L>R){
            ans.push_back(-1);
            ans.push_back(-1);
        }
        else{
            ans.push_back(L);
            ans.push_back(R);
        }
        return ans;
    }
};

在这里插入图片描述

704. 二分查找

题目: 给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例:

示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

解题思路

查找排序（升序）数组nums中，target出现的位置，使用二分查找
首先利用双指针，确定查找的区域的范围[left,right]。其中数组nums[0]为left, nums最后一个元素为right。
然后利用二分法查找：将目标值target与[left,right]中间位置mid: (left+rigjt)/2 的元素比较大小，如果nums[mid] < target, 说明在[0,mid]范围的值都小于target；因此target 范围只能在[mid+1,right]范围内，所以此时left = mid+1; 同理如果nums[mid] > target, 说明target 范围只能在[left,mid-1]范围内, 因此此时right = mid-1
迭代二分查找的过程:while(left <=right) ，直到查找到target, 当二分查找全部遍历完后，此时left = right时，还没有查找到target，说明数组中不存在和target匹配的值
找到target时，此时left = right = mid
注意：二分查找，需要数组本身是排序好的(升序或降序)，本题是针对升序数组

c++ 实现

class Solution {
public:
	int search(vector<int> &nums,int target)
	{
		int left =0;
		int right = nums.size()-1;
		int mid;
		while(left <=right)
		{
			mid = (left +right)/2;
			if(nums[mid] < target)  left = mid +1;
			else if(nums[mid] > target)  right = mid -1;
			else 
			{
				return mid;
			}
		}
		return -1;
	}

};

35.搜索插入位置

题目：给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例：

示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4

示例 4:
输入: nums = [1,3,5,6], target = 0
输出: 0

示例 5:
输入: nums = [1], target = 0
输出: 0

解题思路

对于排序的数组，查找目标值target，首先想到的就是二分查找。
设定查找的边界[left,target],以及中间位置mid
遍历并更新查找的区域:(while (left <=right))，如果left =right=mid(因为mid=(left+right)/2), 说明二分查找已经完成。如果数组中存在目标，target的位置等于left或者right或者mid。
如果二分查结束，目标值不存在于数组中，返回它将会被按顺序插入的位置，也就是返回left值。

c++实现

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;
        while(left <= right)
        {
            int mid = left + (right - left)/2;
            if(nums[mid] < target)
            {
                left = mid + 1;
            }
            else 
            {
                right = mid - 1;
            }
        }
        return left;
    }
};

153. 寻找旋转排序数组中的最小值

题目: 已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次旋转后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次的结果为数组[a[n-1], a[0], a[1], a[2], ..., a[n-2]]。

给你一个元素值互不相同的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例:
在这里插入图片描述

解题思路

c++实现

实现1

class Solution {
public:
    int findMin(vector<int>& nums) {
        return *min_element(nums.begin(),nums.end());
    }
};

实现2
查找旋转次数就好了 (不懂!!!)

class Solution {
public:
    int findMin(vector<int>& nums) {
        if(nums.empty()) return -1;
        int n = nums.size(),r = n-1,l = 0;
        // find k 旋转次数
        while(l<r)
        {
            int m = l + (r -l)/2;
            if(nums[m] < nums[r]) r = m;
            else l = m+1;
        }
        return nums[l];
    }
};

88. 合并两个有序数组

题目: 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你合并 nums2 到 nums1 中，使合并后的数组同样按非递减顺序排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例:
在这里插入图片描述

解题思路

从nums1最后位置开始排
对比nums1和nums2, 谁大先排谁

注意：m=0 或n =0的情况

c++ 实现

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int last = m+n -1;

        while(n)
        {
            if (m==0 || nums1[m-1] <nums2[n-1])  nums1[last--] = nums2[--n];
            else  nums1[last--] = nums1[--m];
        }

    }   
};

240. 搜索二维矩阵 II

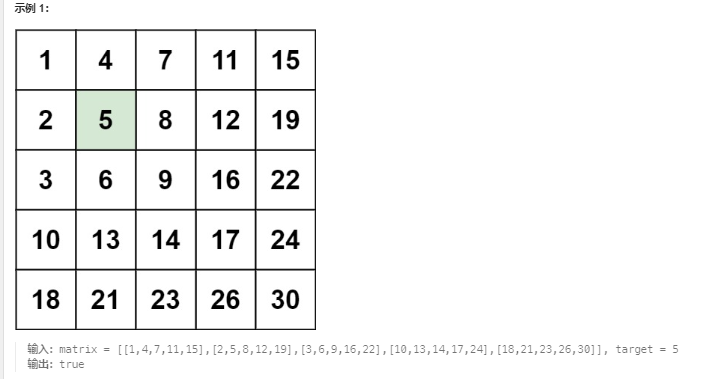
题目:编写一个高效的算法来搜索 m x n 矩阵matrix中的一个目标值 target。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

解题思路

这种矩阵都要从右上角分析，小的往左，大的往下即可

首先就是要选择一个点，使得横向和纵向移动，martix能够有不同的变化
- 左上角：往右往下移动，martix值都变大，无法区分，不可用
- 右上角：往左martix变小，往下martix变大，可区分，可用
- 左下角：往右martix变大，往上martix变小，可区分，可用
- 右下角：往左往上移动，martix都变小，不可区分，不可用

一般都是选择右上角开始分析。

c++实现

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int i = 0, j = matrix[0].size() - 1;
        while (i < matrix.size() && j >= 0) {
            if (matrix[i][j] > target)
                j--;
            else if (matrix[i][j] < target)
                i++;
            else
                return true;
        }
        return false;
    }
};

189.轮转数组

题目: 给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例:
在这里插入图片描述

解题思路

思路1：

通过一个逆置数组元素的函数(reverse)来辅助轮转，首先整个数组进行逆置，然后前后两部分分别进行逆置，当然这里的前后两部分是根据轮转的个数k来划分的。

思路2：

建立一个两倍原数组长度的数组，然后其中保存两遍原数组中的元素，轮转的过程就可以看成是在这个新数组中截取一个原数组长度的数组的过程，具体点说就是根据轮转关系从新数组中截取旧数组长度个数的元素并将这些元素保存到旧数组中。

思路3：

直接写一个双循环，外层循环次数为轮转个数，内层循环每次将数组元素统一向后移一位，在这之前数组最后一个元素已被变量保存，在这之后将此变量的值赋给数组第一个空间，这样一次轮转就已完成，按此完成外循环次数即可。但是这个写法不能通过，因为当数组长度过长时会超出时间限制。

c++ 实现

解题1

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        reverse(nums.begin(),nums.end());
        reverse(nums.begin(),nums.begin()+k%nums.size());
        reverse(nums.begin()+k%nums.size(),nums.begin()+nums.size());
    }
};

在这里插入图片描述

解题2：

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
      vector<int> temp;
      temp.reserve(2*nums.size());
      int len = nums.size();

      for(int i=0;i<len;i++)
      {
          temp[i] = nums[i];
          temp[i+len] = nums[i];
      }

      for(int i=0;i<len;i++)  
           nums[i] =temp[i+len-k%len];
     }
};

在这里插入图片描述

解题3

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        
         for(int i=0;i<k%nums.size();i++) {
            int temp=nums[nums.size()-1];
            for(int j=nums.size()-2;j>=0;j--) {
                nums[j+1]=nums[j];
            }
            nums[0]=temp;
        }
    }
};

在这里插入图片描述
https://blog.csdn.net/qq_42364307/article/details/121429461

74. 搜索二维矩阵

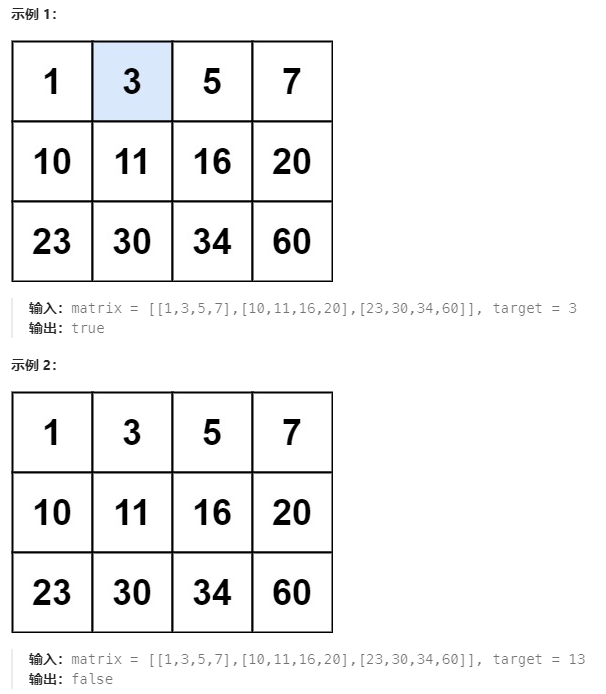
题目：给你一个满足下述两条属性的m x n整数矩阵：

每行中的整数从左到右按非严格递增顺序排列。
每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target ，如果 target 在矩阵中，返回true；否则，返回 false 。

示例:
在这里插入图片描述

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int n = matrix.size(), m = matrix[0].size();
        int l = 0,r = n*m-1;
        while(l<=r){
            int mid = l + (r - l)/2;
            int row = mid/m, col = mid%m;
            if(matrix[row][col] >target) r = mid-1;
            else if(matrix[row][col] <target) l = mid+1;
            else return true;
        }
   
        return false;

        
    }
};

注意：

int mid = l + (r - l)/2;
int row = mid/m, col = mid%m;

不要错写成如下代码:

int mid = l + (r - l)/2;
int row = mid/m-1, col = mid%m-1;

因为首先：r = n*m-1已经做了减1操作了。所以col = mid%m-1是错的。
另外，mid/m会进行向下求整，所以也不需要减1，所以，row = mid/m-1是错的。

986. 区间列表的交集

题目：给定两个由一些 闭区间组成的列表，firstList 和secondList，其中firstList[i] = [starti, endi]而 secondList[j] = [startj, endj] 。每个区间列表都是成对不相交 的，并且 已经排序 。

返回这两个区间列表的交集 。

形式上，闭区间 [a, b]（其中 a <= b）表示实数 x 的集合，而 a <= x <= b 。

两个闭区间的交集是一组实数，要么为空集，要么为闭区间。例如，[1, 3] 和 [2, 4] 的交集为 [2, 3] 。
示例:
在这里插入图片描述

解题思路

首先理一下思路啊，就是我们去比较左边界值，和右边界值。取左边的最大值和右边的最小值，两个夹杂的就是公共区间。
在这里插入图片描述
其中要考虑的一个容易出错的问题就是，下一步如何进行，我们这里就是看谁的右边界的更小，更小的话我们就是需要跑入到下一个区间了。

c++实现

解法1

class Solution {
public:
    vector<vector<int>> intervalIntersection(vector<vector<int>>& firstList, vector<vector<int>>& secondList) {
        vector<vector<int>> res;
        if (firstList.empty() || secondList.empty()) return res;

        int len_1 = firstList.size();
        int len_2 = secondList.size();

        for(int i=0;i< len_2;i++)
        {
            for (int j=0; j< len_1;j++)
            {
                if (secondList[i][0]>firstList[j][1] || secondList[i][1] < firstList[j][0]) continue;
                else res.push_back({max(secondList[i][0],firstList[j][0]),min(secondList[i][1],firstList[j][1])});
            } 
        }

        return res;
    }
};

在这里插入图片描述

解法2：

class Solution {
public:
    vector<vector<int>> intervalIntersection(vector<vector<int>>& firstList, vector<vector<int>>& secondList) {
        vector<vector<int>> result;
        int i = 0, j = 0;
        while (i < firstList.size() && j < secondList.size()) {
            int start = max(firstList[i][0], secondList[j][0]);
            int end = min(firstList[i][1], secondList[j][1]);
            if (start <= end) {
                result.push_back({start, end});
            } 
            if (firstList[i][1] < secondList[j][1]) {
                i++;
            } else {
                j++;
            }
        }
        return result;
    }
};