2022-03-2 出行计划 差分和前缀和

这题很久之前做过一次，现在已经基本忘记了，所以重新做一遍，然后一遍就过了，也算是有了一些进步了。

思路

这题要是暴力的话时间复杂度是$O(n^2)$ 然后数据量是$10^5$ 那么总的时间就是$10^{10}$超过了1s，估计是会超时的，所以就想着如何优化一下。

他每次的区间查询，我们其实可以做下预处理，就是我们其实可以提前算出来所有的q能够满足出行计划的数量呢？因为计划已经确定了，不会再改变了。然后用q这个数组存起来。

那么如何提前算q呢？ 我们可以遍历每个出行计划，那么我们就可以知道在哪个区间内的q可以增加1个出行计划，然后如何进行整个区间的加减操作呢？使用差分复杂度是O(1)就可以。

最后根据输入的q在去除q数组的数即可也是O(1)

最终的时间复杂度也就是O(n)可以满足题目要求。

遇到的问题（不小心出现的细节问题）

1. 没有搞清楚一个出行计划可行的做核酸的时间的区间

我原本以为可行的区间是t~t+c，后来发现是错误的，不是往前满足而是之前的才能满足

也就是区间是 t-c+1~t这个区间里的

2. 一些蠢错误

计算最大的时间（看q 的最大区间是啥）是这个

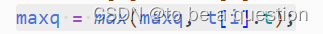
而不是

3. 没有注意到k的应用

做了核酸之后要等k 个时间单位，但是不影响，因为每个做的核酸都是要等k个单位，而且核酸的有效时间也是从k个单位之后才开始计算的。

只需要在最后输出的时候加一个k即可

然后就可以100分了

完整代码

#include <bits/stdc++.h>
using namespace std;
int n, m, k;
int q[400001]; // 用差分进行区间操作
struct trip_plan
{
    int t, c;
} t[100001];
int main()
{
    cin >> n >> m >> k;
    int maxq = -1;
    for (int i = 0; i < n; i++)
    {
        cin >> t[i].t >> t[i].c;
        maxq = max(maxq, t[i].t);
    }
    // 计算差分
    for (int i = 0; i < n; i++)
    {
        q[t[i].t + 1] -= 1;
        q[max(0, t[i].t - t[i].c + 1)] += 1;
    }
    // 计算前缀和 恢复数组的原本意义
    for (int i = 1; i <= maxq + 1; i++)
    {
        q[i] += q[i - 1];
    }
    for (int i = 0; i < m; i++)
    {
        int temp;
        cin >> temp;
        cout << q[temp + k] << endl;
    }
    return 0;
}