系列文章目录

机器学习（一） -- 概述

机器学习（二） -- 数据预处理（1-3）

机器学习（三） -- 特征工程（1-2）

机器学习（四） -- 模型评估（1-4）

未完待续……

---

目录

---

前言

tips：此处以下所有内容均为暂定，因为我还没找到一个好的，让小白（我自己）也能容易理解（更系统、嗯应该是宏观）的讲解顺序与方式。

第一文主要简述了一下机器学习大致有哪些东西（当然远远不止这些），对大体框架有了一定了解。接着我们根据机器学习的流程一步步来学习吧，掐掉其他不太用得上我们的步骤，精练起来就4步（数据预处理，特征工程，训练模型，模型评估），其中训练模型则是我们的重头戏，基本上所有算法也都是这一步，so，这个最后写，先把其他三个讲了，然后，在结合这三步来进行算法的学习，兴许会好点（个人拙见）。

---

一、线性回归通俗理解及定义

1、什么叫线性回归（what）

线性回归（Linear Regression）简单来讲，就是用一条线尽量去“拟合”一组数据。求得的这条线（模型），可以用于预测其他未出现的数据。

2.***一些性质

咱把“线性回归”拆分一下，拆成“线性”、“回归”，这里的“线性”是一类模型，“线性模型”；“回归”是一类问题，“回归问题”，这样“线性回归”就可以是“用线性模型来解决回归问题”。

以下为一些概率性质：

线性（线性关系）：指量与量之间按比例、呈直线关系。

        

        非线性：不按比例、不呈直线关系。

        简单理解线性就是里面的变量都是一次的，即n元一次方程，非线性就是可以高于一次的。
        线性关系和线性模型：线性关系一定是线性模型，线性模型不一定是线性关系。

回归：回归分析，建立一个数学模型来描述因变量和自变量之间的关系。和分类分析是相对的，预测结果是连续的。（数学上叫自变量、因变量，机器学习上叫特征值、目标值）

        分类：预测结果是离散的。

拟合：就是把平面上一系列的点，用一条光滑的曲线连接起来。

        请结合【机器学习（四） -- 模型评估（1）一.3】理解过拟合和欠拟合

尽量拟合就是可以有一定误差，不一定要每个点都经过，这和“过拟合”有关。

3、线性回归的目的（why）

找到一条这样一条拟合数据的直线。
如直线是y=wx+b，x是特征值，y是目标值，我们就是要求出一组w和b。

回归问题：前面说过，可以简单的把回归问题和分类问题区分为：回归问题的预测结果是连续的，分类问题的预测结果是离散的。

***回归问题来源：英国科学家高尔顿（Galton）在研究身高的遗传关系时发现了一种“趋中效应”：
        父亲高于平均身高时，其儿子的身高比他更高的概率要小于比他更矮的概率；
        父亲矮于平均身高时，其儿子的身高比他更矮的概率要小于比他更高的概率。
简单来说就是身高回归平均值。“回归”一词也就是这么来的。

4、如何找这条线（How）

我们的方法是：

1、随机画一条直线，作为初始的直线
2、检查一下它的拟合效果，
3、如果不是最好的（达到阈值），就调整直线位置和角度
3、重复第2、3步，直到最好效果（到达设定的阈值），最终就是我们想要的模型。

其中有两个问题如何检查模型拟合效果、如何调整模型位置角度：
针对检查模型拟合效果，我们一般比较预测值与真实值之间的差值（均方误差，MSE）——最小二乘问题
针对调整模型位置角度，我们采用——梯度下降法

最小二乘问题：这是一个最优化问题，我们要使总的误差尽可能的小。把每一个预测值减去真实值的平方相加，在除以数据量，我们要使这个值最小。

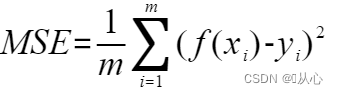
梯度下降法：也叫最速下降法。梯度（函数增长速度最快的方向/方向导数取最大值的方向）。
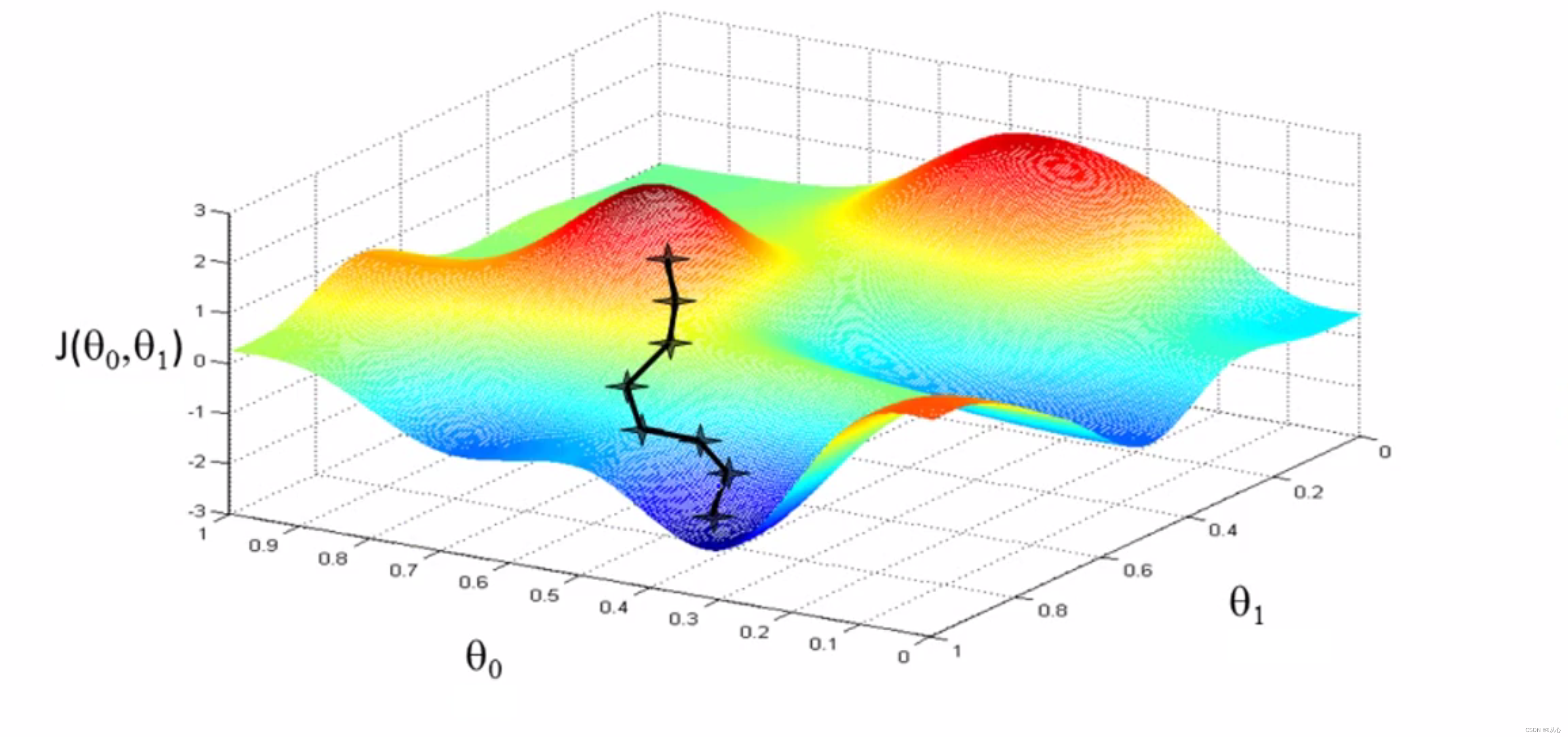形象的理解是你站在山上，想要用最快的方式下山，当然是那里最陡，朝哪走最快，，在数学中就是导数啦，在一个3维立体图中，我们应该朝着当前点梯度的反方向前进。当然也不是随便走多远的，万一你天生神力，从山的一边跳到了另一座山更高的地方也是不行的（步长问题），，步子太大就容易跳过最优解，甚至使误差逐渐变得更大，步长太小又会使下山（找到最优解）的速度变得极慢。

二、原理理解及公式

        和我们切身相关的线性回归例子就是：学科成绩=50%*平时成绩+50%*考试成绩。（在此祝愿小伙伴们，有考试的每门课都是55开，555，37开的哭了QwQ），
        最常接触应该是房价预测问题，房子价格=0.02*中心区域的距离+0.04*城市一氧化碳浓度+0.12*自住房平均价格+0.254*城镇犯罪率

线性回归分为单变量线性回归和多变量（多元）线性回归哟，（简单来说，就是一元一次方程和n元一次方程的区别）

1、单变量线性回归

（Linear Regression with One Variable）

先用单变量线性回归来讲，按照上面的步骤咱一步一步来：

1.1、定义模型

我们可以知道模型是这样的：，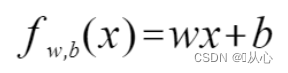

（这里需要严谨一点了，f(x)是模型预测值，y是真实值）

1.2、目标函数

最小二乘法：使用均方误差（MSE）来判定距离，应该使所有观察值的残差平方和达到最小，即代价函数（cost function）采用平方损失函数用的是，则代价函数为

（！！！这里乘了个1/2是为了后面计算方便。）

然后我们就得到了目标函数（objective function）：

结合之后通过调整参数使模型更加贴合真实数据：

（arg min：（argument of the minimum）最小值的参数）

***补充：残差平方和（RSS）：等同于SSE（误差项平方和），实际值与预测值之间差的平方之和。
               均方误差（MSE）：是RSS的的期望值（或均值），（就是乘了个1/m）

***补充：损失函数：是定义在单个样本上的，单个样本的误差。
               代价函数：是定义在整个训练集上的，是所有样本误差的平均，也就是损失函数的平均（让代价函数最小）。（有时，也可以认为损失函数就是代价函数）
               目标函数：最终需要优化的函数，等于经验风险+结构风险（也就是代价函数 + 正则化项，正则项在后面才会用到）。

1.3、参数估计

求w、b使代价函数最小化的过程，称线性回归模型的最小二乘“参数估计”（parameter estimation）。

1.3.1、梯度下降法

梯度下降法（Gradient Descent，GD）：前面也说过梯度是函数增长速度最快的方向/方向导数取最大值的方向，而梯度下降就是要沿着梯度的反方向调整参数，还记得梯度公式吧，梯度是个向量，后面那杂七杂八的一堆是我之前做的笔记，看前面就行。  

多维的有点复杂，我们用如下的一个简单例子来理解如何进行梯度下降，我们假设横坐标是参数，纵坐标为均方误差，红色标记为初始参数，蓝色为其导数，从上面的公式可以看出梯度就是各个方向的偏导数组成的变量，在这个单变量的例子中梯度可以简单理解成就是其导数。

在此例子中，函数曲线为y=x^2，初始参数为w=7，其导数为-14，显然我们要进行梯度下降，就应该向梯度相反方向调整参数，即向右边移动，向导数相反方向移动，是不是就可以用原参数减去导数即可，这里有一个步长问题，上面也说过，所以为了控制步长（在机器学习中称为学习率）要用原参数减去学习率乘以导数，本例中的公式表达就是这个样子：

关于α（学习率）一般需要手动设置，学习率太小，学习太慢；学习率太大，可能无法收敛，甚至发散；常考虑0.001、0.003、0.01、0.03、0.1、0.3、1、3、10。

***一个小特点：当接近局部最低点时，梯度下降法会自动采用更小幅度（因为导数在变化）。

好了我们知道了他的原来，带回原模型得到的参数更新表达式如下：

（为了同步实现更新，需要如上进行参数传递）

将代价函数代入得到（这里其实吧1/m去掉问题也不大，反正α是手动设置，把α设置成原来的mα是一样的意思）：

！！！注意：有的教材可能得到的是如下，这里两者都是正确的哈，只是因为因为在损失函数中f(w,b)和y的相减位置不同导致的。

还有这种表达方式（简单理解，“ := ”就是将左边赋值给右边）：

2、多变量（多元）线性回归

多变量（多元）线性回归（Linear Regression with Multiple Variable）：也叫多重回归（多变量）。其实只是一个特征值变成了多个特征值的情况。

（！！！注意：多变量时往往要进行特征缩放，因为保持相近的梯度，有助于梯度下降算法快速收敛）

2.1、定义模型

多个特征，模型可以用向量表示

也有这种表示（b=w0，x0=1）：

2.2、目标函数

损失函数：

目标函数：

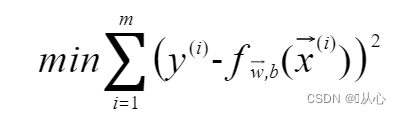
2.3、参数估计

多变量线性回归的参数更新表达式如下：

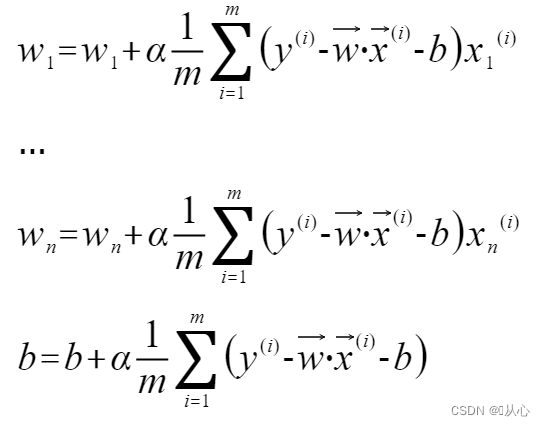
 梯度下降法的缺点 ：刚才的例子只是一个最简单的例子，但在实际情况中往往不是，如下图梯度下降法容易陷入局部最优解：

所以实际应用中往往采用其他方法。

2.3.1、随机梯度下降法

随机梯度下降法（Stochastic Gradient Descent，SGD）选择随机一个训练数据，并使用它来更新参数。参数更新表达式变为（1/m去掉了，为了简便一点）：

***注意：因为是随机的一个数字，这里的上标不是i了，而是随机数k，（又get一个小细节，哦耶）。

优点：最速下降法更新 1 次参数的时间，随机梯度下降法可以更新 n 次。
           随机梯度下降法由于训练数据是随机选择的，更新参数时使用的又是选择数据时的梯度，所以不容易陷入目标函数的局部最优解。

2.3.2、批量梯度下降法

批量梯度下降法：类似，只是数据不是全部也不是一个，而是一小部分，参数更新表达式变为

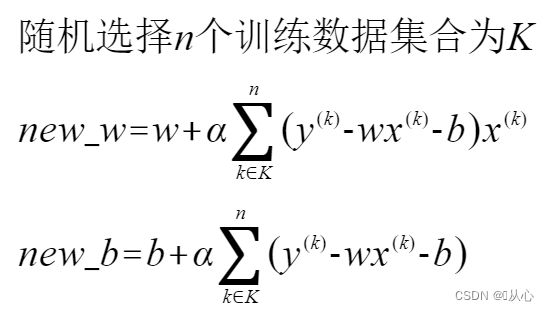
2.3.3、正规方程

梯度下降法是对代价函数的每个参数求偏导，通过迭代算法一步步更新，直到收敛到全局最小值，从而得到最优参数。正规方程是一次性求得最优解。

思想是对于一个简单函数，对参数求导，将其值直接设置为0，就得到参数的值。如下图：

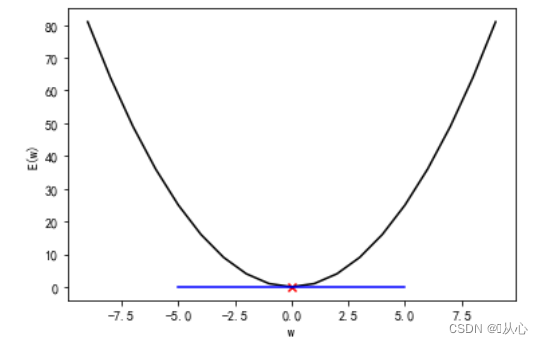
通过求解方程来找出使得代价函数最小的参数的，（这里用θ更好表示所有参数）

即这里的模型设为这种形式：

损失函数则为：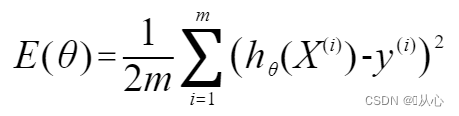

***推导过程：

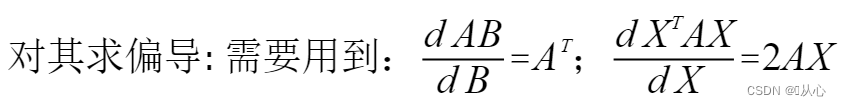
最后得到，可以一次运算出参数

正规方程的优点：

        1、不需要学习率α

        2、一次计算即可，不用多次迭代

正规方程的缺点：

        1、需要计算，如果特征数量较大，运算代价大矩阵逆的时间复杂度为 O(n^3) ，通常小于10000可以接受。

        2、只适用于线性模型

3、多项式回归

多项式回归（高次项）：线性回归不适用所有数据，有时需要曲线来适应数据。

（多项式回归时，特征缩放也是很有必要的。）

定义模型

其他步骤也是类似。

三、代码实现

1、***算法实现

为了加深理解哈，其实在日常中一般调用API。

1.1、读入数据

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib notebook

# 读入数据
train =pd.read_csv('csv/click.csv')
train_x=train['x']
train_y=train['y']

# 查看数据
plt.figure()
plt.scatter(train_x,train_y,c='r',marker='.')
# plt.plot(train_x,train_y,'ro')
plt.show()

 

1.2、定义模型

 

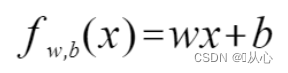
# 预测函数-定义模型
def f(x):
    return theta0+theta1*x

1.3、目标函数

# 目标函数
def E(x,y):
    return 0.5*np.sum((y-f(x))**2)

 

1.4、参数估计

先进行标准化，后绘图验证

# 标准化、z-score规范化
mu = train_x.mean()
sigma = train_x.std()
def standardize(x):
    return (x - mu) / sigma

train_z=standardize(train_x)

# 绘图
plt.figure()
plt.plot(train_z,train_y,'go')
plt.show()

参数初始化、学习率等的设置

# 参数初始化
theta0=np.random.randn()
theta1=np.random.randn()

# 学习率
ETA = 1e-3 # 0.001

# 误差的差值
diff = 1

# 更新次数
count = 0

# 重复学习
error = E(train_z, train_y)
while diff > 1e-2:
    # 更新结果保存到临时变量(防止更新1时使用更新后的0)
    tmp_theta0 = theta0 - ETA * np.sum((f(train_z) - train_y))
    tmp_theta1 = theta1 - ETA * np.sum((f(train_z) - train_y) * train_z)

    # 更新参数
    theta0 = tmp_theta0
    theta1 = tmp_theta1

    # 计算与上一次误差的差值
    current_error = E(train_z, train_y)
    diff = error - current_error
    error = current_error

    # 输出日志
    count += 1
    log = '第 {} 次 : theta0 = {:.3f}, theta1 = {:.3f}, 差值 = {:.4f}'
    print(log.format(count, theta0, theta1, diff))

# 绘图确认
x = np.linspace(-3, 3, 100)# 定义均匀间隔创建数值序列

plt.figure()
# 数据点
plt.plot(train_z, train_y, 'o')
# 模型
plt.plot(x, f(x))
plt.show()

 

 1.5、验证

# 验证
x1=standardize(100)
y1=f(x1)
print(y1)     # 370.9798855192978

plt.plot(x1,y1,'*')

2、接口调用--实际应用

2.1、加载数据（划分数据集）

# 加载所需函数
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
# 加载boston数据
boston = load_boston()
x = boston['data']
y = boston['target']
names = boston['feature_names']

# 将数据划分为训练集测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=125)

2.2、建立模型

# 建立线性回归模型
clf = LinearRegression().fit(x_train, y_train)
print('建立的LinearRegression模型为：', '\n', clf)

 

2.3、预测结果

# 预测测试集结果
y_pred = clf.predict(x_test)
print('预测前20个结果为：', '\n', y_pred[:20])