总述

并查集（Disjoint-set Union，简称并查集）是一种用来管理元素分组情况的数据结构。它主要用于解决集合的合并与查询问题，通常涉及到以下两种操作：

1. 合并（Union）： 将两个集合合并成一个集合。
2. 查询（Find）： 查找某个元素所属的集合。

并查集通常应用于解决连接问题，如判断无向图中的连通分量、网络连接状态的判断、社交网络中的好友关系等。在算法竞赛和数据结构课程中也经常会涉及到并查集的应用场景，比如 Kruskal 算法中的边权值排序，以及求解最小生成树等。

合并过程

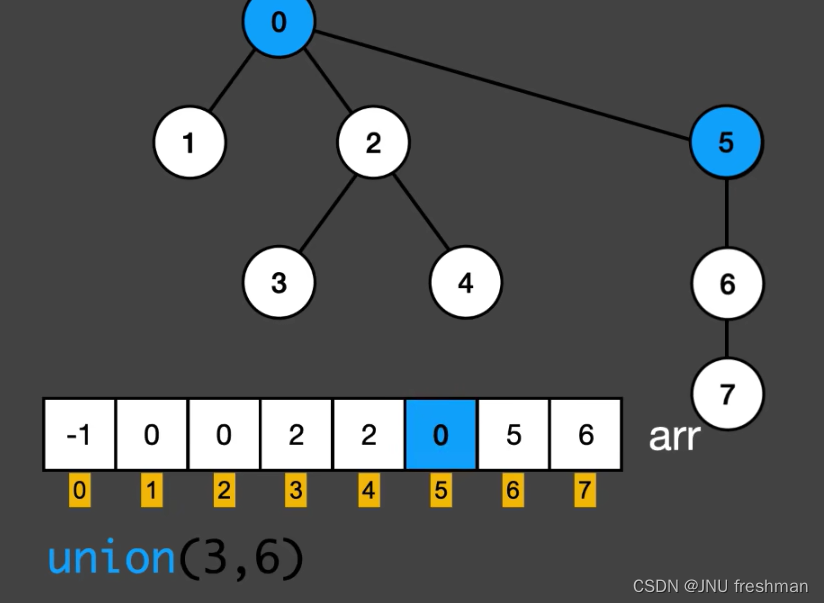
• 合并的过程就是先找到两个元素的根，若根不相同则将其中的一个根的父节点改成另一个根节点

s = [i for i in range(N+1)]  # 列表s[i] 表示i 节点的父节点，开始的时候，全部指向自己
def union(x,y):
	r1 = find(x)
	r2 = find(y)
	if r1 != r2:
		s[r1] = s[r2]
	

查找过程

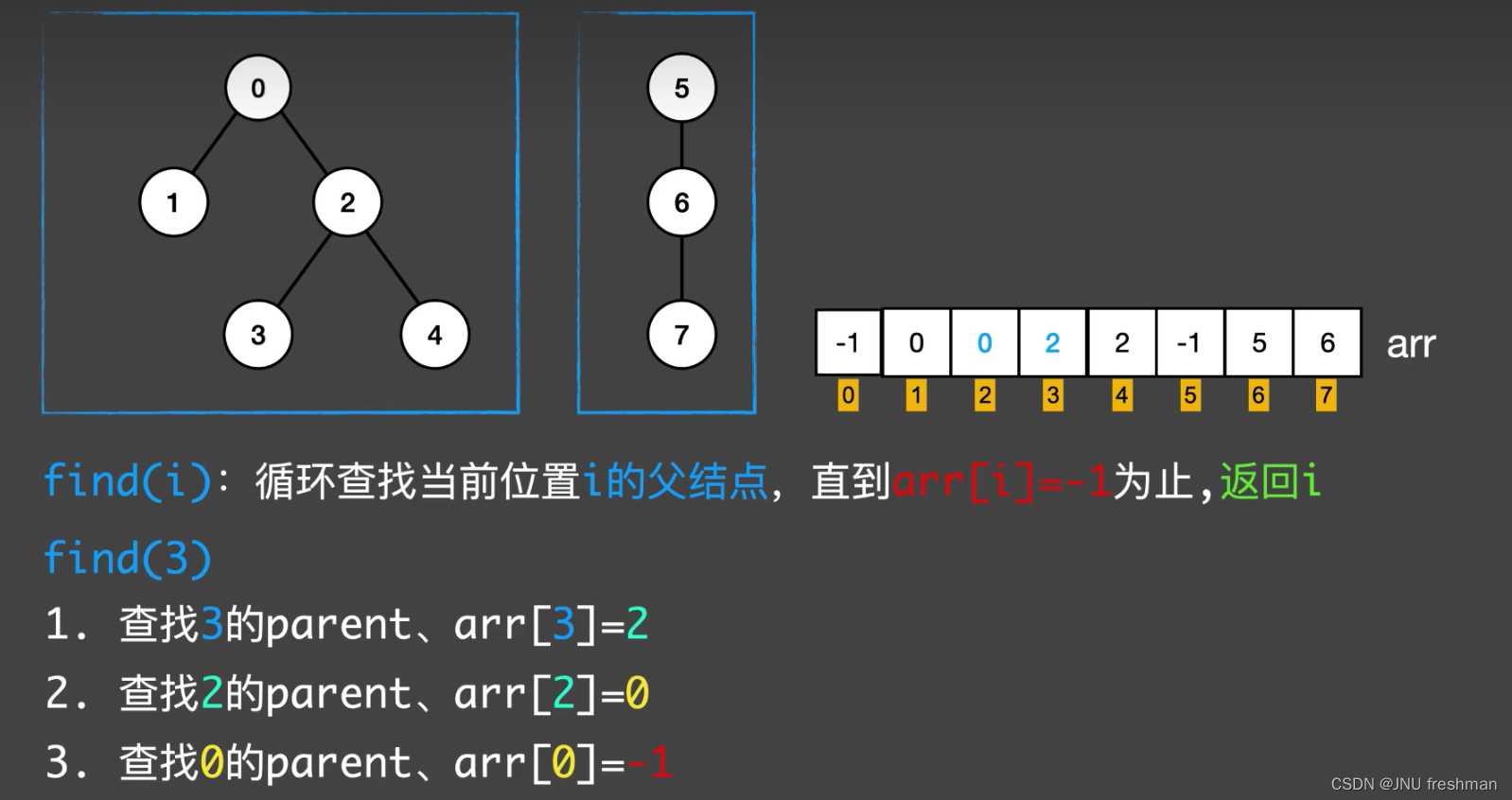
• 对于查找的过程，就是一直找

def find(x):  # 返回 x 的根节点
	if x != s[x]:
		s[x] = find(s[x])
	return s[x]

算法实战

实战1

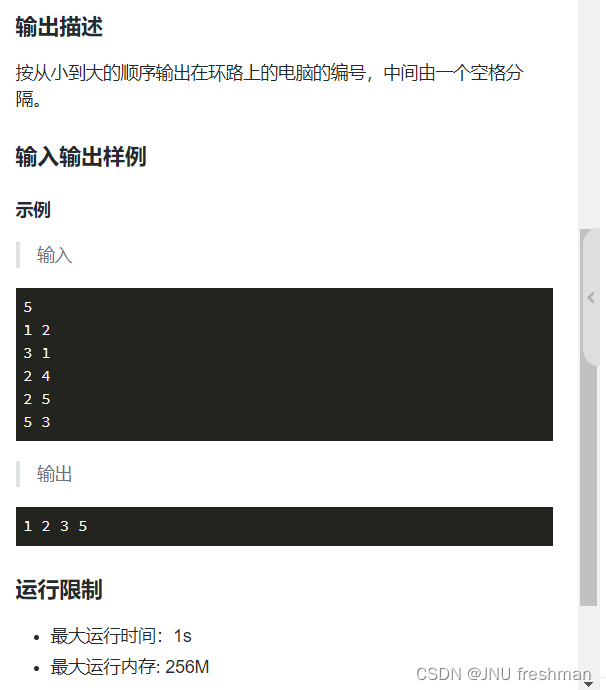
from collections import defaultdict

n = int(input())
p = [i for i in range(n + 1)] # p[i] 表示 节点 i 的父节点
tree = defaultdict(list) # 输入键，当键不存在就生成键：列表
used = [0] * (n + 1) # 用来记录是否访问过
ans = [0] * n  # 用来反复记录路径


def find(x):    # 并查集的查找函数，返回x 节点的根
    if x != p[x]:
        p[x] = find(p[x])
    return p[x]


def dfs(pos, idx):
    ans[idx] = pos
    if pos == end:
        res = sorted(ans[:idx + 1]) # 排序
        print(' '.join(map(str, res))) # 输出，间隔空格输出 
        return

    for d in tree[pos]: # 逐一访问节点的邻接节点
        if not used[d]: # 由于是无向图，并且加上深度搜索，所以要记录一个节点是否已经访问过
            used[d] = 1
            dfs(d, idx + 1)


for _ in range(n):
    u, v = map(int, input().split()) 
    tu, tv = find(u), find(v) 
    if tu == tv:
        start, end = u, v  
        break  # 所以是不必加载全部的边的关系的，因为当两个输入的节点的根相同的时候，就说明已经包含环了
    else:
        p[tv] = tu
        tree[u].append(v)
        tree[v].append(u) # 无向图

used[start] = 1
dfs(start, 0) 

代码分析

• 不能直接暴力地去深度搜索，会超时
• 用并查集来判断两个节点是否位于不同的连通分支
• 并查集并不是死板地运用全部的合并和查找函数
• 深度搜索只是一种工具并不是死板地运用全部的框架