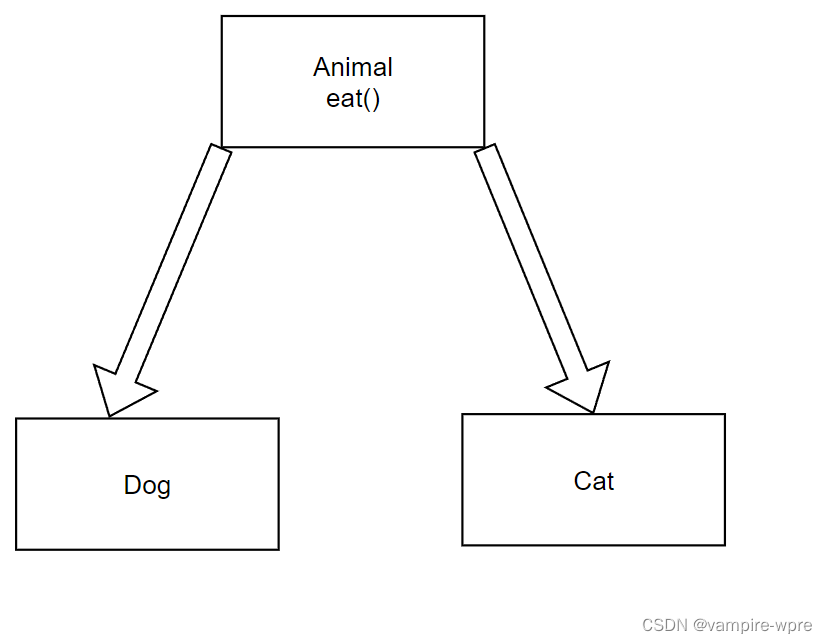
递归是用来做dfs,是搜索算法的基础
递推是用来做dp部分,及部分其他算法,复杂度较低,不会出现爆栈问题
递推法:
递推法是一种在数学和其他领域广泛应用的重要方法,它在计算机科学中被用作一种关键的数值求解算法。
递推算法的特点
递推法的核心在于找到递推关系式。这种方法可以将复杂的计算过程转化为简单的重复步骤,充分利用计算机在运行程序时的时间局部性和空间局部性。
递推算法的思想:
- 首先找到各个相邻数据项之间的递推关系;
- 递推关系避开了求通项公式的麻烦,尤其是对于那些难以或无法求解通项公式的题目;
- 将复杂问题分解为若干步骤的简单运算;
- 一般来说,递推算法可以视为一种特殊的迭代算法。
递推算法解题的基本思路:
- 将复杂计算转换为简单重复运算;
- 通过找到递推关系式进行简化运算;
- 利用计算机的特性,减少运行时间。
递推算法的一般步骤:
- 根据题目确定数据项,并找到符合要求的递推关系式;
- 根据递推关系式设计递推程序;
- 根据题目找到递推的终点;
- 单次查询可以不进行存储,多次查询都要进行存储;
- 按要求输出答案即可。
递归法
递归算法:
递归算法是一种自顶向下的算法,它通过不断地直接或间接调用自身的函数,通过每次改变变量完成多个过程的重复计算,直到到达边界之后,结束调用。
与递推法相似的是,递归与递推都是将一个复杂过程分解为几个简单重复步骤进行计算。
递归算法的实现的核心是分治策略,即分而治之,将复杂过程分解为规模较小的同类问题,通过解决若干个小问题,进而解决整个复杂问题。
递归算法的思想:
- 将复杂计算过程转换为简单重复子过程;
- 找到递归公式,即能够将大问题转化为小问题的公式;
- 自上而下计算,在返回完成递归过程。
递归算法设计的一般步骤:
- 根据题目设计递归函数中的运算部分;
- 根据题目找到递归公式,题目可能会隐含给出,也可能需要自己进行推导;
- 找到递归出口,即递归的终止条件。
递归法和递推法的思路已经给大家讲解得差不多了,接下来我们将结合真实的大赛题目进行讲解。这将有助于我们更好地理解和应用这两种方法。
1. 斐波纳契数列 fibonacci 问题
在一定情况下,同一个问题可以使用用递归也可以使用递推解答。一般一个问题的递推关系和递归关系都好求的话就都可以解题。
当然如果题目只有一个关系好求,那就最好采用关系好求的办法。
题目描述:
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”。
指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、…
在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1,F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N^*)
请求出该数列中第n个数字(n从1开始计数)是多少。
样例:
输入样例
样例1输入
6
样例2输入
4
输出样例
样例1输出
8
样例2输出
3
对于上面的样例我们进行了如下计算;
[0]=0
[1]=1
[2]=0+1
[3]=1+1=2
[4]=1+2=3
[5]=2+3=5
[6]=5+3=8
运行限制:
1. 最大运行时间:1s
2. 最大运行内存:128M
题目解析:
- 这个题给出递推式 F(n) = F(n-1) + F(n-2)
- 转化为可用的递推关系,即F(n) + F(n+1) = F(n+2)
这一通过从n=1开始循环即可完成递推,当然也可以使用递归法。
首先我们写找出递归式,F(n)= F(n-1) + F(n-2)
F(n)= F(n-1) + F(n-2)
= F(n-2)+F(n-3)+F(n-3)+F(n-4)
//重复调用
这样我们找到了递归式,然后我们应该找到递归出口。
我们可以知道 F(n)=0 n=0 ,F(n)=1 n=1这就是递归出口,能让递归停止的条件。
递归算法的通用框架如下:
do(a,b,c...)
{
//递归终止条件,即出口
if(a==? ,b==? ,....) return
//递归条件
if(条件1)
do(参数1)
else(条件2)
do(参数2)
}
如本题,各子式间存在计算关系,可以化为:
do(a)
{
if(a==0) return 0;
if(a==1) return 1;
return do(a-1)+do(a-2);
}
这道题不是多次询问问题,不需要存储直接计算的复杂度是最低的。
答案解析
C++ 代码:
- 递推算法代码
#include <iostream>
using namespace std;
int main()
{
int n; //第几个数
int x=0; //F(n)
int y=1; //F(n+1)
int ans; //F(n+2)
cin>>n;
if(n==0) ans=0;
else if(n==1) ans=1;
else {
for(int i=2;i<=n;i++)
{
ans=x+y;
x=y;
y=ans;
}
}
cout<<ans<<endl;
}
- 递归算法代码
#include <iostream>
using namespace std;
int fn(int n)
{
//递归出口1
if(n==0)
return 0;
//递归出口2
else if(n==1 )
return 1;
else
return fn(n-1)+fn(n-2); //递归关系式
}
int main()
{
int n; //第几个数
int ans;
cin>>n;
ans=fn(n);
cout<<ans<<endl;
}
改进:记忆化
递归过程中做了重复工作,例如fib(3)计算了两次,其实只算1次就够了
为避免递归时重复计算,可以在子问题得到解决时,就保存结果,再次需要这个结果时,直接返回保存的结果就行了,不继续递归下去
这种存储已经解决的子问题结果的技术称为记忆化
记忆化是递归的常用优化技术
动态规划也常常使用递归写代码,记忆化也是动态规划的关键技术
#include <bits/stdc++.h>
using namespace std;
int cnt = 0; //统计执行了多少次递归
int data[25]; //存储斐波那契数
int fib (int n)
{
cnt++;
if (data[n] != 0) //记忆化搜索,已经算过,不用再算,直接返回结果
return data[n];
if (n == 1 || n == 2)
{
data[n] = 1;
return data[n];
}
data[n] = fib(n - 1) + fib(n - 2); //继续递归
return data[n];
}
int main()
{
cout << fib(20); //计算递20个斐波那契数
cout << " cnt=" << cnt; //递归了cnt = 37次
}
存储型的递推与递归
我们在开始就讲过题目十分存储和非存储的,上面那个题目就是此询问,如果改为多次询问我们该怎么办,我们会采用存储的方式,存储的方式适用于大部分的的多次查询问题。
我们看一下修改后的题目。
题目描述:
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”。
指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……
在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1,F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)
我们将进行M次查询,每次输入一个N,其中n小于30。
请求出该数列中第n个数字(n从1开始计数)是多少?
样例:
输入样例
样例1输入:
6
4
2
7
8
8
10
样例2输入:
8
13
23
14
17
24
16
10
11
输出样例
样例1输出:
3
1
13
21
21
55
样例2输出:
233
28657
377
1597
46368
987
55
89
运行限制:
1. 最大运行时间:1s
2. 最大运行内存:128M
题目解析:
这道题跟上面一道题的算法原理相同,只是增加了多次查询的复杂度,所以仅需修改这一点即可。
再有的是有的同学担心自己的输入输出是在一个屏幕上的,评测的时候会不会出现问题。
类似这样的情况,这一点是不用担心的,只要不是交互题,评测机的输入与输出是分开的,只有你的输出会用来跟答案比较,所以我们只用关心我们的输出即可。
比如有一道题让你计算 x+y 的值,如果你知道每答案,就可以直接输出,都不用进行读入。
然后我们来看一下需要多次询问的题目该怎么解决。
答案解析
C++ 代码:
递推算法代码
#include <iostream>
using namespace std;
int F[35];
void init()
{
F[0]=0;
F[1]=1;
for(int i=2;i<=30;i++)
{
F[i]=F[i-1]+F[i-2];
}
}
int main()
{
int m; //m次查询
int n; //第几个数
init();
cin>>m;
while(m>0)
{
m-=1;
cin>>n;
cout<<F[n]<<endl;
}
}
存储答案的递推法,才是最常使用的递推法。
递归算法代码
#include <iostream>
using namespace std;
int F[35];
int fn(int n)
{
//递归出口1
if(n==0)
{
F[0]=0;
return 0;
}
//递归出口2
else if(n==1 )
{
F[1]=1;
return 1;
}
else
{
F[n]=fn(n-1)+fn(n-2);
return F[n]; //递归关系式
}
}
int main()
{
int m; //m次查询
int n; //第几个数
fn(30);
cin>>m;
while(m>0){
m-=1;
cin>>n;
cout<<F[n]<<endl;
}
}
数字三角形问题
题目描述:

如图数字三角形。如下所示为一个数字三角形。请编一个程序计算从顶到底的某处的一条路径,使该路径所经过的数字总和最大。只要求输出总和。
- 一步可沿左斜线向下或右斜线向下走;
- 三角形行数小于等于 100;
- 三角形中的数字为 0,1,…,99;
测试数据通过键盘逐行输入。
如上例数据应以样例所示格式输入:
样例:
输入:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输出:
30
运行限制:
1. 最大运行时间:1s
2. 最大运行内存:128M
题目分析:
N=100,
S=
(
1
+
100
)
∗
100
=
1
0
4
(1+100)*100=10^4
(1+100)∗100=104
量级是
1
0
4
10^4
104,每个数都是0-99
最后是
1
0
6
10^6
106,用暴力也能做出来
解决该题目的方式有很多,包括动态规划, 枚举都可以解决这个问题。
我们从递推的思想出发,假设我们从顶层沿着某条路径已经走到了第 i 层,正向着 i+1 层前进, 两条可行路径中我们肯定会选择最大的方向前进,
为此我们可以采用递推中的反向递推,即逆推的方式解决,设
a
[
i
]
[
j
]
a[i][j]
a[i][j]存放从
i
,
j
i,j
i,j 出发到达第
n
n
n 层的最大值。
我们可以写出递推式:
a[i][j] = max{a[i][j]+a[i+1][j],a[i][j]+a[i+1][j+1]}
则 逆推到出发点
a
[
1
]
[
1
]
a[1][1]
a[1][1]为题目所求答案,即第一层到第
N
N
N层的最大值。
递推一层由
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
逆推第一层
7
3 8
8 1 0
7 12 10 10
第二层
7
3 8
20 13 10
第三层
7
23 21
第四层
30
递推的每次计算是 O ( 1 ) O(1) O(1), i i i是层数, j j j是 i i i层的这几个
C++ 代码:
#include<iostream>
using namespace std;
int main()
{
int n; //n层
int a[101][101]; //路径矩阵
cin>>n;
//输入数字三角形的值
for (int i=1; i<=n; i++)
{
for (int j=1; j<=i; j++)
{
cin>>a[i][j]; //输入原始数据
}
}
//递推开始
for (int i=n-1; i>=1; i--)//从最后一层逆推
{
for (int j=1; j<=i; j++)
{
if (a[i+1][j]>=a[i+1][j+1])
a[i][j]+=a[i+1][j]; //路径选择
else
a[i][j]+=a[i+1][j+1];
}
}
cout<<a[1][1]<<endl;
}
递推法的推广
42点问题
题目描述
众所周知在扑克牌中,有一个老掉牙的游戏叫做 24 点:选取4 张牌进行加减乘除,看是否能得出 24 这个答案。
现在小蓝同学发明了一个新游戏,他从扑克牌中依次抽出6张牌(注意不是一次抽出),进行计算,看是否能够组成 42 点,满足输出 YES,反之输出 NO。
最先抽出来的牌作为第一个操作数,再抽出牌做第二个操作数,运算结果再当作第一个操作数,继续进行操作。除不尽的情况保留整数。
请你设计一个程序对该问题进行解答。
输入描述
输出仅一行包含 6 个字符。
保证字符∈3 4 5 6 7 8 9 10 J Q K A 2。
输出描述
若给出到字符能够组成 42 点,满足输出 YES,反之输出 NO。
题目解析
不是一次抽出,可以重复,有放回事件
数据输入
for (int i = 0; i < 6; i++)
{
char c;
cin >> c;
if (c == 'A')
a[i] = 1;
else if (c == 'J')
a[i] = 11;
else if (c == 'Q')
a[i] = 12;
else if (c == 'K')
a[i] = 13;
else
a[i] = (c - '0');
}
怎么枚举5次运算
共计
4
∗
4
∗
4
∗
4
∗
4
=
1024
4*4*4*4*4=1024
4∗4∗4∗4∗4=1024种情况
创建5个vector,分别用来存放1-5次的运算结果
vector <int> ans[10];
ans[0].push_back(a[0]);
for (int i = 1; i <= 5; i++)
{
for (int j = 0; j < ans[i-1].size(); j++)
{
ans[i].push_back(ans[i-1][j]+a[i]);
ans[i].push_back(ans[i-1][j]-a[i]);
ans[i].push_back(ans[i-1][j]*a[i]);
ans[i].push_back(ans[i-1][j]/a[i]);
}
}
判断
int flag = 0;
for (int i = 0; i < ans[5].size(); i++)
{
if (ans[5][i] == 42)
{
flag = 1;
break;
}
}
if (flag == 1)
cout << "YES" << endl;
else
cout << "NO" << endl;
数的计算
题目描述
我们要求找出具有下列性质数的个数(包含输入的自然数 n):
先输入一个自然数
n
(
n
≤
1000
)
n(n \le 1000)
n(n≤1000),然后对此自然数按照如下方法进行处理:
- 不作任何处理:
- 在它的左边加上一个自然数,但该自然数不能超过原数的一半:
- 加上数后,继续按此规则进行处理,直到不能再加自然数为止。
例:n=6,合法的数字有:6(不做任何处理)、16、26、36、126、136
题目解析
第一层递归,枚举
a
=
1
,
2
,
…
,
n
2
a=1,2,\dots,{\frac{n}{2}}
a=1,2,…,2n
第二层递归,枚举
b
=
1
,
2
,
…
,
a
2
b=1,2,\dots,{\frac{a}{2}}
b=1,2,…,2a
第三层递归,枚举
c
=
1
,
2
,
…
,
b
2
c=1,2,\dots,{\frac{b}{2}}
c=1,2,…,2b
…
最后一层,等于1,返回
6
6/2=3 构造出 16 26 36
再根据16,a=1 构造不出来了,1/2=0
再根据26,a=2 构造2/2=1,构造出126
再根据126,1/2=0,构造不出来了
再根据36,构造3/2=1,构造出136
136不能再产出新数字
void f (int n)
{
if (n == 1)
return; //如果n = 1,满足条件的数的个数是1
for (int i = 1; i <= n/2; i++) //枚举左边加的数
{
res++; //新得到一个数,满足条件的数的个数+1
f(i); //递归
}
}
按照题目意思,我们可以直接枚举左边加的数。
定义递归函数 f(n)表示输入数为 n 时满足题目条件的数的个数。
我们可以从最简单的情况开始考虑。当n =1时,只有一个数,满足条件的数的个数是 1。
如果 n > 1,那么我们需要枚举左边加的数。因为最左边的数不能为 0,所以左边加上的数的取值范围是
[
1
,
n
/
2
]
[1,{n/2}]
[1,n/2]
对于每一个加数i,得到的新数是n+i,我们需要递归调用 f(n +i),计算得到新数下满足条件的数的个数。
在递归调用结束后,我们需要将所有加数得到的满足条件的数的个数相加,得到最终的结果。
最后,输出 f(n)即可。
N=1时,1/2=0,无法进行构造,就只有一个解
N=2时,2/2=1,恰好构造出了12和本身2
N=3时,3/2=1,恰好构造出了13和本身3
N=4时,4/2=2,能够构造出14 24 124 4
如果写成函数
f(4) = f(4/2=2)+f(2/2=1)+1 //124 24 / 14 / 4
f(5) = f(5/2=2)+f(2/2=1)+1 //125 25 / 15 / 5
...
f(n) = f(n/2)+f(n/2/2)+...+f(1)+1
递归式:
F(n):
用i=(1-n/2)构造;
对于每个生成的新的i,再次调用f(i)
每构造一次就+1
代码
#include <iostream>
using namespace std;
int f[1000];
int main()
{
int n;
scanf("%d", n);
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= i/2; j++)
{
f[i] = f[i] + f[j];
}
f[i] = f[i] + 1;
}
return 0;
}
数的划分
题目描述
将整数 n 分成k份,且每份不能为空,任意两份不能相同(不考虑顺序)。
例如:n=7,k=3,下面三种分法被认为是相同的。
1,1,5;
1,5,1;
5,1,1;
问有多少种不同的分法。
输入描述
输入一行,2 个整数 n,k (6 ≤n≤ 200,2 ≤k≤ 6)。
输出描述
输出一个整数,即不同的分法
题目解析
计数dp,分治思想
7
4,2,1
定义递归函数
f
(
n
,
m
)
f(n,m)
f(n,m)为将整数 n 拆分成 m 个数字的方案数。
对于每个情况,我们可以将它分成两种情况,且这两种情况是不重不漏的。
- 不选1的情况
如果不选择 1,我们将 n 拆分成 m 块,可以等价于将每一块都减去 1,然后再将剩下的数拆分成m块,即 f ( n − m , m ) f(n-m,m) f(n−m,m)。 - 选1的情况:
这种情况下,其中一块肯定有一个 1,然后对几-1拆分成 m-1块,即 f ( n − 1 , m − 1 ) f(n-1,m-1) f(n−1,m−1)。
此时, f ( n , m ) f(n,m) f(n,m)的值就是这两种情况之和,即
f ( n , m ) = f ( n − m , m ) + f ( n − 1 , m − 1 ) f(n,m)=f(n-m,m)+f(n-1,m-1) f(n,m)=f(n−m,m)+f(n−1,m−1)
对于样例7分3份:
- 不选1,那就先每份给个1
111剩下了4,由于不选1,所以每组还得再分至少一个,所以就变成 f ( n − m , m ) f(n-m,m) f(n−m,m),即 7 − 3 = 4 7-3=4 7−3=4分成3份 f ( 4 , 3 ) f(4,3) f(4,3)
对于 f ( 4 , 3 ) f(4,3) f(4,3)在考虑递归过程,同样分两种情况-
f
(
4
,
3
)
=
f
(
4
−
3
,
3
)
+
f
(
4
−
1
,
3
−
1
)
f(4,3)=f(4-3,3)+f(4-1,3-1)
f(4,3)=f(4−3,3)+f(4−1,3−1)
- f(1,3)不合理,所以没有这种可能返回0
-
f
(
3
,
2
)
=
f
(
3
−
2
,
2
)
+
f
(
3
−
1
,
2
−
1
)
f(3,2)=f(3-2,2)+f(3-1,2-1)
f(3,2)=f(3−2,2)+f(3−1,2−1)
- f ( 1 , 2 ) f(1,2) f(1,2)不合理返回0
- f ( 2 , 1 ) f(2,1) f(2,1)两个数分成1堆,只有一种办法返回1
-
f
(
4
,
3
)
=
f
(
4
−
3
,
3
)
+
f
(
4
−
1
,
3
−
1
)
f(4,3)=f(4-3,3)+f(4-1,3-1)
f(4,3)=f(4−3,3)+f(4−1,3−1)
- 选1的情况,有且只能有1个1,所以1那个位置就不再改变,我们就去考虑剩下的7-1个数,分成3-1份,那就变成了
f
(
n
−
1
,
m
−
1
)
f(n-1,m-1)
f(n−1,m−1)即
f
(
6
,
2
)
f(6,2)
f(6,2)
对于 f ( 6 , 2 ) f(6,2) f(6,2)使用同样的递归过程继续执行
代码
#include <bits/stdc++.h>
using namespace std;
int f(int n, int m)
{
if (n == 0 || m == 0 || n < m)
{
return 0;
}
if (m == 1 || n == m)
{
return 1;
}
else
{
return f (n - m, m) + f(n - 1, m - 1);
}
}
int main()
{
int n, k;
cin >> n >> k;
cout << f (n, k) << "\n";
return 0;
}
过多分支的一种处理思路
题目描述
古代中国使用天干地支来记录当前的年份。
天千一共有十个,分别为:甲、乙、丙、丁、戊、己、庚、辛、王、癸 。地支一共有十二个,分别为:子、丑、寅、卯、辰、日、午、未、申、酉、戌、亥将天干和地支连起来,就组成了一个天干地支的年份,例如:甲子。
2020 年是庚子年。
每过一年,天干和地支都会移动到下一个。例如2021年是辛丑年。
每过 60年,天千会循环6轮,地支会循环5轮,所以天干地支纪年每 60年轮回一次。例如 1900年,1960年,2020年都是庚子年给定一个公元纪年的年份,请输出这一年的天干地支年份。
输入描述
输入一行包含一个正整数,表示公元年份。
其中有 ,输入的公元年份为不超过9999的正整数。
输出描述
输入一行包含一个正整数,表示公元年份。
这个题目是模拟法中最讨厌也最常见的一种,可能还有比这更复杂的,但这道题,已经初具代表性
他的种类比较多,天干就有10种,地支有12种
现在我们知道了 2020年是庚子年,我们这里既可以是除留余数来判断N年是什么天干和什么地支,我们也可以直接暴力使用循环做,这样的话9999的复杂度也跑不了多久。
实现起来很简单,我们讲这个比较难的。
我们先判断0000年的天干和地支
根据题意8000年距2020年了2020年。
已知天干有10个,那么2020%10=0剩下的都是整个轮回,即到了0000年是庚X年,即天干是庚,
再按照这个方法算地支是2020%12=4及还要向前推四年地支为申。
即 0000 为申年,那么根据模拟法可知。
string tg(int n)
{
n = n%10;
if (n == 0)
return "geng";
}
string dz(int n)
{
...
}
string tg[10] = {"geng"."xin","ren","gui","jia","yi","bing","ding","wu","ji"};
string dz[12] = {"shen","you","xu","hai","zi","chou","yin","mou","chen","si","wu","wei"};
int main()
{
int year;
cin >> year;
cout << tg[year%10] << dz[year%12] << endl;
}