1 蛇梯问题
Snake and Ladder Problem
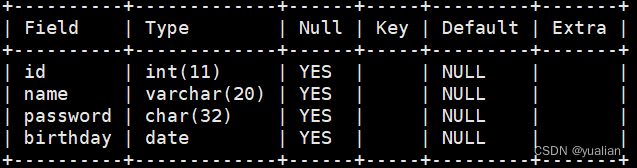
给定一个蛇梯板,找出从源单元格或第一个单元格到达目标单元格或最后一个单元格所需的最小掷骰次数。基本上,玩家可以完全控制掷骰子的结果,并希望找出到达最后一个单元格所需的最小掷骰次数。
如果玩家到达的牢房是梯子的底部,玩家必须爬上梯子,如果到达的牢房是蛇的嘴,则必须在不掷骰子的情况下下下到蛇的尾巴。
例如,考虑所示的电路板,从单元1到达单元30所需的最小掷骰子次数为3。
以下是步骤:
a) 首先掷两个骰子到3号牢房,然后爬到22号牢房
b) 然后掷6到28。
c) 最终通过2达到30。
还有其他解决方案,如(2,2,6),(2,4,4),(2,3,5)。。等
其思想是将给定的蛇梯板视为顶点数等于板中单元数的有向图。问题归结为在图中寻找最短路径。如果接下来的6个顶点没有蛇或阶梯,则图的每个顶点都有一条到下6个顶点的边。如果接下来的六个顶点中有任何一个具有蛇或阶梯,则当前顶点的边将到达阶梯的顶部或蛇的尾部。由于所有边的权重相等,我们可以使用图的宽度优先搜索有效地找到最短路径。
以下是上述想法的实施情况。输入由两个东西表示,第一个是“N”,它是给定电路板中的单元数,第二个是大小为N的数组“move[0…N-1]”。如果没有snake,也没有来自i的梯形图,则条目move[i]为-1,否则move[i]包含snake或位于i的梯形图的目标单元索引。

2 源程序
using System;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
public class Entry
{
public int v { get; set; } = 0;
public int dist { get; set; } = 0;
public Entry()
{
}
}
public class Snakes_Ladder_Problem
{
public static int Minium_Dice_Throws(int[] move)
{
int n = move.Length;
int[] visited = new int[n];
Queue<Entry> q = new Queue<Entry>();
Entry qe = new Entry();
visited[0] = 1;
q.Enqueue(qe);
while (q.Count != 0)
{
qe = q.Dequeue();
int v = qe.v;
if (v == (n - 1))
{
break;
}
for (int j = v + 1; j <= (v + 6) && j < n; j++)
{
if (visited[j] == 0)
{
Entry a = new Entry();
a.dist = (qe.dist + 1);
visited[j] = 1;
if (move[j] != -1)
{
a.v = move[j];
}
else
{
a.v = j;
}
q.Enqueue(a);
}
}
}
return qe.dist;
}
}
}

3 源代码
using System;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
public class Entry
{
public int v { get; set; } = 0;
public int dist { get; set; } = 0;
public Entry()
{
}
}
public class Snakes_Ladder_Problem
{
public static int Minium_Dice_Throws(int[] move)
{
int n = move.Length;
int[] visited = new int[n];
Queue<Entry> q = new Queue<Entry>();
Entry qe = new Entry();
visited[0] = 1;
q.Enqueue(qe);
while (q.Count != 0)
{
qe = q.Dequeue();
int v = qe.v;
if (v == (n - 1))
{
break;
}
for (int j = v + 1; j <= (v + 6) && j < n; j++)
{
if (visited[j] == 0)
{
Entry a = new Entry();
a.dist = (qe.dist + 1);
visited[j] = 1;
if (move[j] != -1)
{
a.v = move[j];
}
else
{
a.v = j;
}
q.Enqueue(a);
}
}
}
return qe.dist;
}
}
}