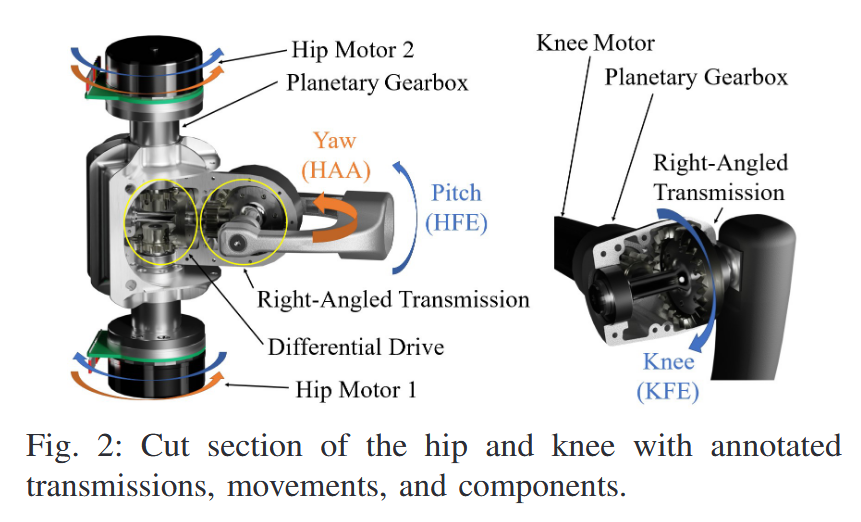
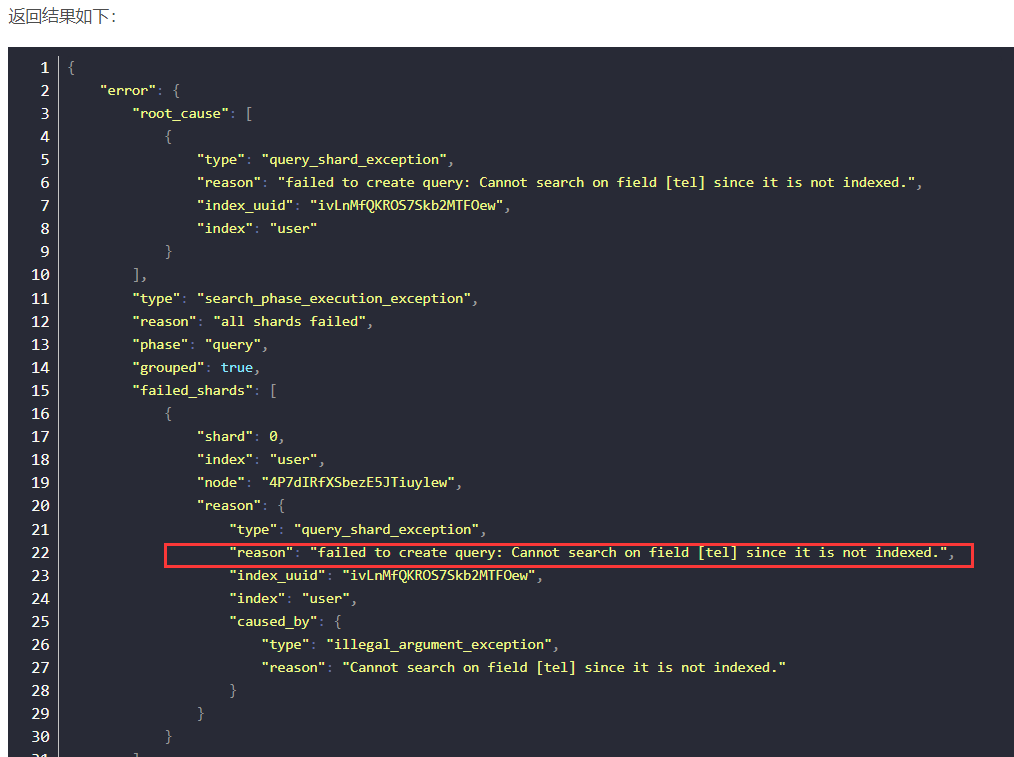
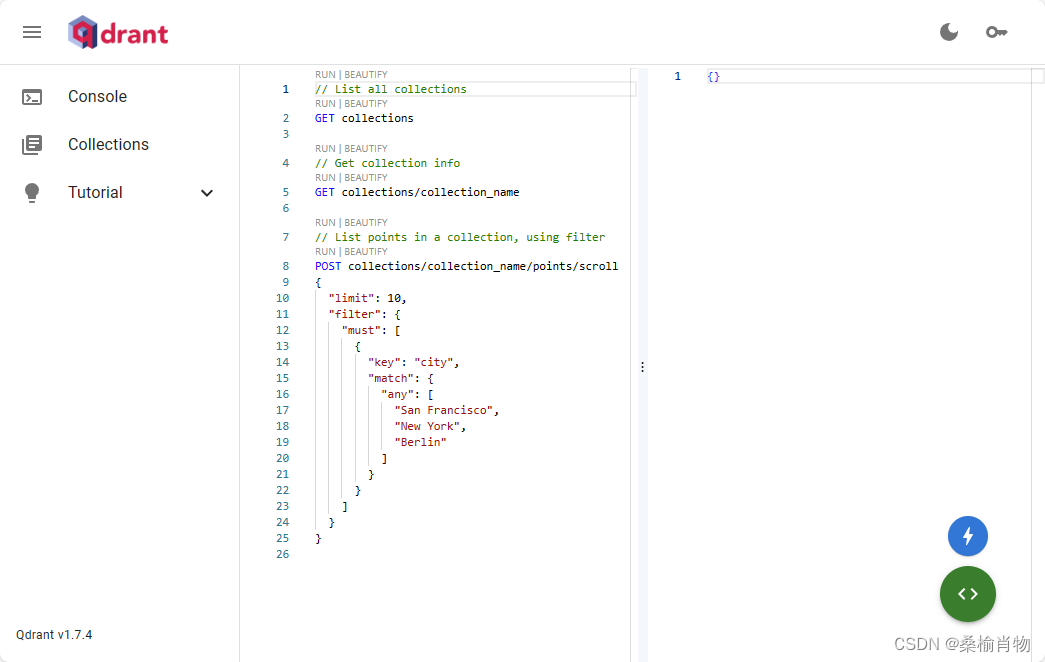
傅里叶变换法

如果令fd(w)为期望方向图，那么对应的电流分布id(s)为

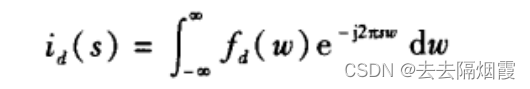
但是，通常它的范围是无穷大的，所以我们通过近似解来截断id(s)如下

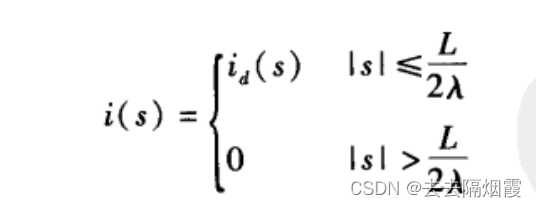
根据傅里叶变化，电流就会产生一个近似方向图f(w)。扩展至整个s域的电流id(s)产生准确的方向图fd(w)

但是傅里叶变化综合所得的方向图在可见区域不能提供最小的均与偏差

例子：扇形方向图的傅里叶变换综合

扇形方向图是一种赋形波束方向图，它可以理想化地在一个主波束（扇形空格区域）内均匀辐射，旁瓣为零。

令他的期望方向图为

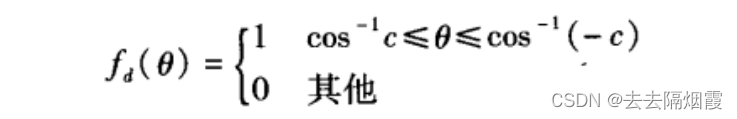
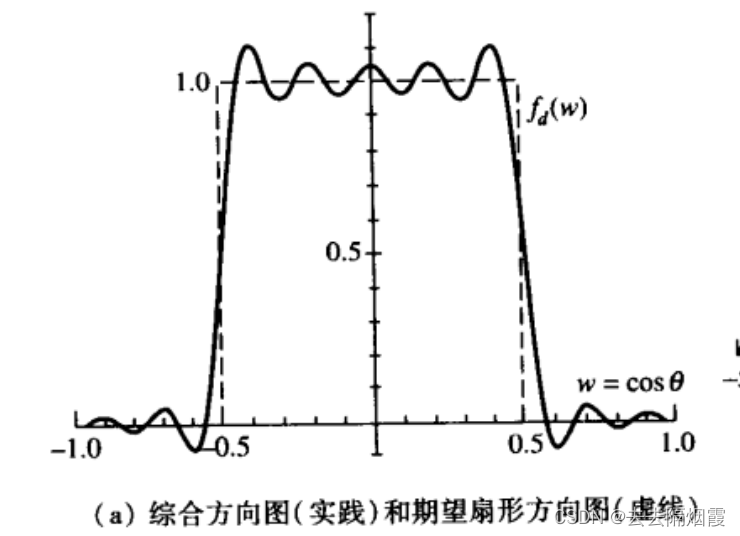
综合方向图为实线，期望方向图为虚线（也就是我们想要的方波）

根据上面期望方向图对应的电流分布公式以及带入扇形方向图的期望方向图公式得出

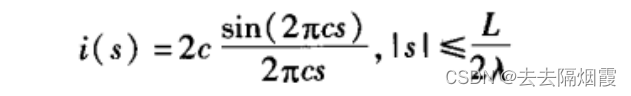
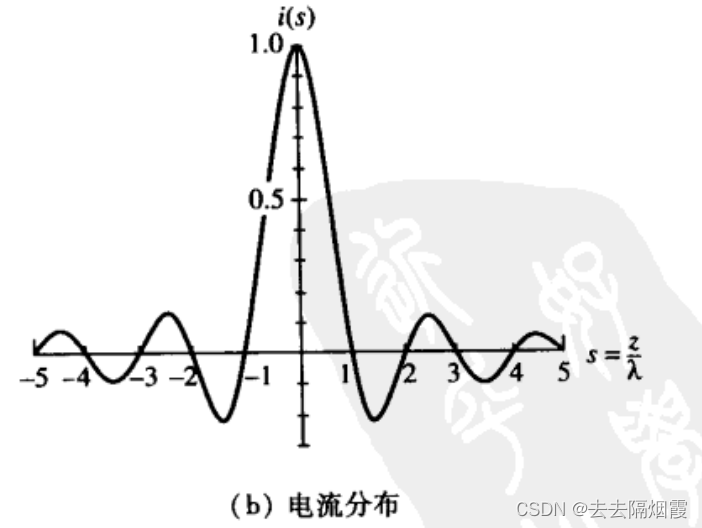
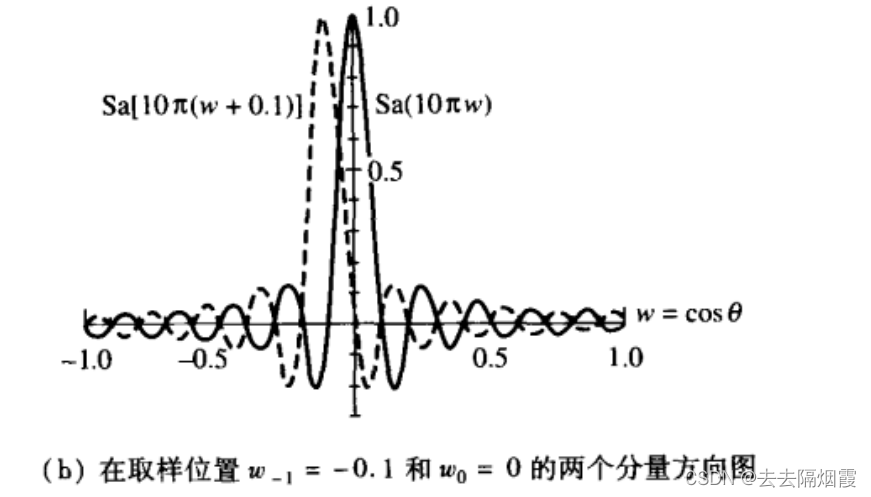
伍德沃德——罗森方法的好处在于当一个取样函数最大时，另外一个取样函数为零，这样使取样相互独立

另外，每个取样函数在除了其最大值位置之外的所有取样点为零，当包含所有取样时，在位置wn的总综合方向图完全由中心位于该位置的Sa函数决定