java 数据结构二叉树

树

树的概念

树的表示形式

二叉树

两种特殊的二叉树

二叉树的性质

二叉树的存储

二叉树的基本操作

二叉树的遍历

二叉树的基本操作

二叉树oj题

树

树是一种 非线性 的数据结构，它是由 n （ n>=0 ）个有限结点组成一个具有层次关系的集合。 把它叫

做树是因为它看 起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的 。它具有以下的特点：

有一个特殊的结点，称为根结点，根结点没有前驱结点

除根结点外，其余结点被分成M(M > 0)个互不相交的集合T1、T2、......、Tm，其中每一个集合Ti

(1 <= i <=m) 又是一棵与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后

继

树是递归定义的

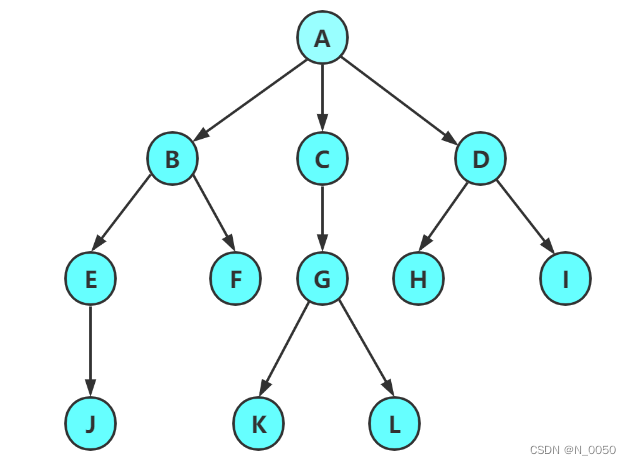
注意：树形结构中，子树之间不能有交集，否则就不是树形结构

一棵树是由若干个不相交的子树组成的

除了根结点之外，每个结点有且只有一个父结点

一棵N个结点的树有N-1条边

树的概念

结点的度：一个结点含有子树的个数称为该结点的度；如上图：A的度为6

树的度：一棵树中，所有结点度的最大值称为树的度；如上图：树的度为6

叶子结点或终端结点：度为0的结点称为叶结点；如上图：B、C、H、I...等节点为叶结点

双亲结点或父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点；如上图：A是B的父结点

孩子结点或子结点：一个结点含有的子树的根结点称为该结点的子结点；如上图：B是A的孩子结点

根结点：一棵树中，没有双亲结点的结点；如上图：A

结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推

树的高度或深度：树中结点的最大层次；如上图：树的高度为4

树的深度和结点的层次是相同的

非终端结点或分支结点：度不为0的结点；如上图：D、E、F、G...等节点为分支结点

兄弟结点：具有相同父结点的结点互称为兄弟结点；如上图：B、C是兄弟结点

堂兄弟结点：双亲在同一层的结点互为堂兄弟；如上图：H、I互为兄弟结点

结点的祖先：从根到该结点所经分支上的所有结点；如上图：A是所有结点的祖先

子孙：以某结点为根的子树中任一结点都称为该结点的子孙。如上图：所有结点都是A的子孙

森林：由m（m>=0）棵互不相交的树组成的集合称为森林

树的表示形式

树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，实际中树有很多种表示方式，

如： 双亲表示法 ， 孩子表示法 、 孩子双亲表示法 、 孩子兄弟表示法 等等。我们这里就简单的了解

其中最常用的 孩子兄弟表示法 。

例子：

class Node {
int value; // 树中存储的数据
Node firstChild; // 第一个孩子引用
Node nextBrother; // 下一个兄弟引用
}

二叉树

一棵二叉树是结点的一个有限集合，该集合：

1. 或者为空

2. 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成

图中看出

1. 二叉树不存在度大于2的结点

2. 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树

注意：对于任意的二叉树都是由以下几种情况复合而成的：

两种特殊的二叉树

满二叉树:

一棵二叉树，如果每层的结点数都达到最大值，则这棵二叉树就是满二叉树。也就是说，如果一棵

二叉树的层数为K，且结点总数是2的k次-1 ，则它就是满二叉树

完全二叉树:

完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n

个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应

时称之为完全二叉树

要注意的是满二叉树是一种特殊的完全二叉树

二叉树的性质

1. 若规定 根结点的层数为 1 ，则一棵 非空二叉树的第 i 层上最多有 (i>0) 个结点

2. 若规定只有 根结点的二叉树的深度为 1 ，则 深度为 K 的二叉树的最大结点数是 (k>=0)

3. 对任何一棵二叉树 , 如果其 叶结点个数为 n0, 度为 2 的非叶结点个数为 n2, 则有 n0 ＝ n2 ＋ 1

4. 具有 n 个结点的完全二叉树的深度 k 为log2（n+1） 上取整

5. 对于具有 n 个结点的完全二叉树 ，如果按照 从上至下从左至右的顺序对所有节点从 0 开始编号 ，

则对于 序号为 i 的结点有 ：

若i>0 ， 双亲序号： (i-1)/2 ； i=0 ， i 为根结点编号 ，无双亲结点

若 2i+1<n ，左孩子序号： 2i+1 ，否则无左孩子

若 2i+2<n ，右孩子序号： 2i+2 ，否则无右孩子

二叉树的存储

二叉树的存储结构 分为： 顺序存储 和 类似于链表的链式存储

二叉树的链式存储是通过一个一个的节点引用起来的，常见的表示方式有二叉和三叉表示方式 ，具

体如下：

// 孩子表示法
class Node {
    int val; // 数据域
    Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
    Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {
    int val; // 数据域
    Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
    Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
    Node parent; // 当前节点的根节点
}

二叉树的基本操作

简单创建一棵二叉树：

public class BinaryTree{
public static class BTNode{
    BTNode left;
    BTNode right;
    int value;
BTNode(int value){
    this.value = value;
}
}
private BTNode root;
public void createBinaryTree(){
    BTNode node1 = new BTNode(1);
    BTNode node1 = new BTNode(2);
    BTNode node1 = new BTNode(3);
    BTNode node1 = new BTNode(4);
    BTNode node1 = new BTNode(5);
    BTNode node1 = new BTNode(6);
    root = node1;
    node1.left = node2;
    node2.left = node3;
    node1.right = node4;
    node4.left = node5;
    node5.right = node6;
}
}

二叉树是：

1. 空树

2. 非空：根节点，根节点的左子树、根节点的右子树组成的

从概念中可以看出，二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现

二叉树的遍历

1. 前中后序遍历

学习二叉树结构，最简单的方式就是遍历。所谓遍历 (Traversal) 是指沿着某条搜索路线，依次对树

中每个结 点均做一次且仅做一次访问 。 访问结点所做的操作依赖于具体的应用问题

遍历是二叉树上最重要的操作之一，是二叉树上进行其它运算之基础。

在遍历二叉树时，如果没有进行某种约定，每个人都按照自己的方式遍历，得出的结果就比较混

乱， 如果按 照某种规则进行约定，则每个人对于同一棵树的遍历结果肯定是相同的 。如果 N 代表根

节点， L 代表根节点的左子树，R 代表根节点的右子树，则根据遍历根节点的先后次序有以下遍历

方式：

NLR ：前序遍历 (Preorder Traversal 亦称先序遍历 )—— 访问根结点 ---> 根的左子树 ---> 根的右子树。

例子：

    // 前序遍历:根-左子树-右子树
    void preOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        System.out.print(root.val + " ");
        preOrder(root.left);
        preOrder(root.right);
    }

LNR ：中序遍历 (Inorder Traversal)—— 根的左子树 ---> 根节点 ---> 根的右子树

例子：

    // 中序遍历:左子树-根-右子树
    void inOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        inOrder(root.left);
        System.out.print(root.val + " ");//对于左子树也是到走到头打印根
        inOrder(root.right);
    }

LRN ：后序遍历 (Postorder Traversal)—— 根的左子树 ---> 根的右子树 ---> 根节点

例子：

    // 后序遍历:左子树-右子树-根
    void postOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.val + " ");
    }

层序遍历 ：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根

节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后

从左到右访问第 2 层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树

的结点的过程就是层序遍历

例子：

    //层序遍历
    void levelOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        //把根存到队列里
        queue.offer(root);

        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            System.out.print(cur.val + " ");
            //如果左树不为空,存到队列里
            if (cur.left != null) {
                queue.offer(cur.left);
            }
            if (cur.right != null) {
                queue.offer(cur.right);
            }
        }
    }

二叉树的基本操作

获取树中节点的个数

    //递归:求整个树的结点树=左子树节点+右子树节点+根
    public int size2(TreeNode root) {
        if (root == null) {
            return 0;
        }
        return size2(root.left) + size2(root.right) + 1;
    }

获取叶子节点的个数

    //递归:获取叶子节点的个数=左子树叶子节点+右子树叶子节点
    int getLeafNodeCount2(TreeNode root) {
        if (root == null) {
            return 0;
        }
        //思路一个根的左子树和它的右子树都为空说明这就是叶子节点
        if (root.left == null && root.right == null) {
            return 1;
        }
        return getLeafNodeCount2(root.left) + getLeafNodeCount2(root.right);
    }

获取第K层节点的个数

    // 获取第K层节点的个数:左树的第K-1层+右树的第K-1层
    int getKLevelNodeCount2(TreeNode root, int k) {
        if (root == null) {
            return 0;
        }
        if (k == 1) {//如果k等于1,说明k走到你想要获取的层了
            return 1;
        }
        return getKLevelNodeCount2(root.left, k - 1) + getKLevelNodeCount2(root.right, k - 1);
    }

获取二叉树的高度

    //就是递归到根没有左右子树后,然后比较左右子树谁大谁加1然后返回给对于它的根
    int getHeight(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftH = getHeight(root.left);
        int rightH = getHeight(root.right);
        return leftH > rightH ? leftH + 1 : rightH + 1;
    }

检测值为value的元素是否存在

    // 检测值为value的元素是否存在
    TreeNode find(TreeNode root, char val) {
        if (root == null) {
            return null;
        }
        if (root.val == val) {//如果根的val等于你要找的就返回
            return root;
        }
        //然后从左边开始找,不是空就返回根进行判断
        TreeNode root1 = find(root.left, val);
        if (root1 != null) {
            return root1;
        }
        TreeNode root2 = find(root.right, val);
        if (root2 != null) {
            return root2;
        }
        return null;
    }

判断一棵树是不是完全二叉树

 public boolean isCompleteTree(TreeNode root) {
        if (root == null) {
            return true;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            if (cur != null) {
                queue.offer(root.left);
                queue.offer(root.right);
            } else {
                //走到这说明为cur指向空
                break;
            }
        }
        //完全二叉树,从上到下,从左到右,不能有间隔
        //如果你是一棵完全二叉树,出现空了,就不会出现其他的
        while (!queue.isEmpty()) {
            TreeNode cur = queue.peek();
            if (cur == null) {
                queue.poll();
            } else {
                return false;
            }
        }
        //队列空了
        return true;
    }

小总结：

目前遇到的这些树的问题就是递归的问题，我们把它想象把每个树都有左子树和右子

树，如果有左右子树，对于树的左子树和右子树，它自己就是根，然后递归到没有为

止，然后开始一个个返回到属于自己的根。

也就是每个结点从某种意义来说就是一个独立的子树

二叉树oj题

检查两棵树是否相同：

https://leetcode.cn/problems/same-tree/

代码：

    public boolean isSameTree(TreeNode p, TreeNode q) {
        if (p == null && q != null || p != null && q == null) {
            return false;
        }
        //上面判断完,要么两个为空,要么不为空,都为空也说明这颗树相同
        if (p == null && q == null) {
            return true;
        }
        //到这里了,说明都不为空
        if (p.val != q.val) {
            return false;
        }
        //走到这里说明结构相同并且值也相同,然后开始判断左右子树
        return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
    }

另一颗树的子树：

https://leetcode.cn/problems/subtree-of-another-tree/

代码：

    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        //先判断是不是空
        if (root == null || subRoot == null) {
            return false;
        }
        //判断根结点相不相同
        if (isSameTree(root, subRoot)) {
            return true;
        }
        //判断左子树相不相同
        if (isSubtree(root.left, subRoot)) {
            return true;
        }
        //判断右子树相不相同
        if (isSubtree(root.right, subRoot)) {
            return true;
        }
        return false;
    }

翻转二叉树：

226. 翻转二叉树 - 力扣（LeetCode）

代码：

    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return null;
        }
        //这样到叶子结点直接返回
        if (root.left == null && root.right == null) {
            return root;
        }
        TreeNode node = root.left;
        root.left = root.right;
        root.right = node;
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }

判断一颗二叉树是否是平衡二叉树：

110. 平衡二叉树 - 力扣（LeetCode）

代码：

    public boolean isBalanced2(TreeNode root) {
        if (root == null) {
            return true;
        }

        return getHeight3(root) >= 0;
    }

    int getHeight3(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftH = getHeight(root.left);
        if (leftH < 0) {
            return -1;
        }
        int rightH = getHeight(root.right);
        //每个节点都要判断是否是平衡二叉树！一旦有一个节点不是平衡二叉树，就要逐层向上返回-1
        if (leftH >= 0 && rightH >= 0 && Math.abs(leftH - rightH) <= 1) {
            return Math.max(leftH, rightH) + 1;
        } else {
            return -1;
        }
    }

对称二叉树

101. 对称二叉树 - 力扣（LeetCode）

代码：

    public boolean isSymmetric(TreeNode root) {
        if (root == null) {
            return true;
        }
        return check(root.left, root.right);
    }

    public boolean check(TreeNode leftTree, TreeNode rightTree) {
        //判断是不是都为空
        if (leftTree == null && rightTree == null) {
            return true;
        }
        //一个为空就说明结构不一样
        if (leftTree == null || rightTree == null) {
            return false;
        }
        //判断根值一不一样
        if (leftTree.val != rightTree.val) {
            return false;
        }
        //判断左子树的左跟右子树的的右
        return check(leftTree.left, rightTree.right) && check(leftTree.right, rightTree.left);
    }

二叉树的构建及遍历：

二叉树遍历_牛客题霸_牛客网 (nowcoder.com)

代码：

class Solution {
    static class TreeNode {
        public int val;
        public TreeNode left;
        public TreeNode right;

        public TreeNode(int val) {
            this.val = val;
        }
    }

    //根据一棵树的前序遍历与中序遍历构造二叉树
    public int preIndex;//定义成 成员变量 这样方法调用的时候不会变

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return createTree(preorder, inorder, 0, inorder.length - 1);
    }

    private TreeNode createTree(int[] preorder, int[] inorder, int inBegin, int inEnd) {
        //当inEnd小于inBegin,说明结点都创建完了
        if (inBegin > inEnd) {
            return null;
        }
        //从preorder前序遍历里创建一个根,每次递归都会创建
        TreeNode root = new TreeNode(preorder[preIndex]);

        //从inorder第二个数组中找出根结点的下标
        int rootIndex = find(inorder, inBegin, inEnd, preorder[preIndex]);
        if (rootIndex == -1) {
            return null;
        }
        //preorder下标往前走
        preIndex++;

        root.left = createTree(preorder, inorder, inBegin, rootIndex - 1);

        root.right = createTree(preorder, inorder, rootIndex + 1, inEnd);
        return root;
    }

    //从inorder第二个数组中找出根结点的下标
    private int find(int[] inorder, int inBegin, int inEnd, int Key) {
        //为什么i <= inEnd,因为上面已经给inEnd赋值为长度减1了
        for (int i = inBegin; i <= inEnd; i++) {
            if (inorder[i] == Key) {
                return i;
            }
        }
        return -1;
    }
}

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先：

236. 二叉树的最近公共祖先 - 力扣（LeetCode）

代码：

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) {
            return null;
        }
        //如果p或者q一开始就在root上,root就是最近公共祖先
        if (root == p || root == q) {
            return root;
        }

        TreeNode leftTree = lowestCommonAncestor(root.left, p, q);

        TreeNode rightTree = lowestCommonAncestor(root.right, p, q);

        //走到这一步,说明p和q要么各自在一侧,要么都在左边,要么都在右边
        if (leftTree != null && rightTree != null) {
            return root;
        } else if (leftTree != null) {
            return leftTree;
        } else {
            return rightTree;
        }
    }

根据一棵树的前序遍历与中序遍历构造二叉树：

105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）

代码：

    public int preIndex;//定义成 成员变量 这样方法调用的时候不会变

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return createTree(preorder, inorder, 0, inorder.length - 1);
    }

    private TreeNode createTree(int[] preorder, int[] inorder, int inBegin, int inEnd) {
        //当inEnd小于inBegin,说明结点都创建完了
        if (inBegin > inEnd) {
            return null;
        }
        //从preorder前序遍历里创建一个根
        TreeNode root = new TreeNode(preorder[preIndex]);

        //从inorder第二个数组中找出根结点的下标
        int rootIndex = find(inorder, inBegin, inEnd, preorder[preIndex]);
        if (rootIndex == -1) {
            return null;
        }
        //preorder下标往前走
        preIndex++;

        root.left = createTree(preorder, inorder, inBegin, rootIndex - 1);

        root.right = createTree(preorder, inorder, rootIndex + 1, inEnd);
        return root;
    }

    private int find(int[] inorder, int inBegin, int inEnd, int preIndex) {
        //为什么i <= inEnd,因为上面已经给inEnd赋值为长度减1了
        for (int i = inBegin; i <= inEnd; i++) {
            if (inorder[i] == preIndex) {
                return i;
            }
        }
        return -1;
    }

二叉树创建字符串：

606. 根据二叉树创建字符串 - 力扣（LeetCode）

代码：

class SolutionTree {
    static class TreeNode {
        public int val;
        public TreeNode left;
        public TreeNode right;

        public TreeNode(int val) {
            this.val = val;
        }
    }

    //根据一棵树的中序遍历与后序遍历构造二叉树
    public int postIndex;

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        postIndex = postorder.length - 1;
        return createTree(inorder, postorder, 0, inorder.length - 1);
    }

    private TreeNode createTree(int[] inorder, int[] postorder, int inBegin, int inEnd) {
        //当inEnd小于inBegin,说明结点都创建完了
        if (inBegin > inEnd) {
            return null;
        }
        //从postorder后序遍历里创建一个根,每次递归都会创建
        TreeNode root = new TreeNode(postorder[postIndex]);

        //从inorder第二个数组中找出根结点的下标
        int rootIndex = find(inorder, inBegin, inEnd, postorder[postIndex]);
        if (rootIndex == -1) {
            return null;
        }
        postIndex--;

        //从右边开始递归
        root.right = createTree(inorder, postorder, rootIndex + 1, inEnd);

        root.left = createTree(inorder, postorder, inBegin, rootIndex - 1);

        return root;
    }

    //从inorder数组中找出根结点的下标
    private int find(int[] inorder, int inBegin, int inEnd, int Key) {
        //为什么i <= inEnd,因为上面已经给inEnd赋值为长度减1了
        for (int i = inBegin; i <= inEnd; i++) {
            if (inorder[i] == Key) {
                return i;
            }
        }
        return -1;
    }
}

总结：二叉树的内容可以说是初阶数据结构难以理解的，基本上都是用递归实现的，需要慢慢练习

才能掌握