阵列信号处理有以下三个研究方向：

1. 检测入射信号是否存在，以及入射信号的数目
2. 检测入射信号的到达方向（DOA)角
3. 增强某个感兴趣方向的信号，抑制其他方向的干扰（beamforming)

波束形成（beamforming）分为窄带波束形成和宽带波束形成。窄带可简单理解为信号只有一个频率，宽带就是信号有无限多个频率。麦克风阵列信号处理就涉及到宽带波束形成。在介绍宽带波束形成之前，我们先介绍窄带波束形成。

窄带波束形成

下图是一个基于线阵的波束形成简单结构，由M个阵元组成的线性阵列，对波场进行空间采样。

输出信号的表达式：

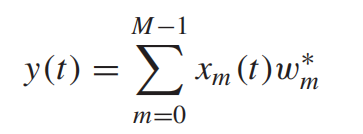
就是第m个阵元采集到的信号，是第m个阵元的权重系数。

对于输入平面波信号是复信号（对应的角频率是），DOA角度是（范围是[  ]）。如上图所示，角是相对于与线性阵列垂直方向定义的。

如果如果第0个阵元采集到的信号是，第个阵元采集到的信号是,  = 1, 2, ... , 。是信号从第0个阵元传播到第个阵元所需的延时。

波束形成器的输出为：

波束形成器的响应为：

向量是个阵元的复共轭系数

称作阵列响应向量（或者转向向量steering vector，方向向量direction vector）

避免时域混叠要求信号的最高频率小于1/2的采样率。避免空域混叠要求阵列之间的距离小于

当时，等间隔线性阵列窄带波束形成器的响应为：

对于与上式相同系数的FIR滤波器，其频率响应为：

是归一化频率，从变化到时，从变化到。

窄带波束形成的实例

设计波束形成器，将波束指向，并且抑制

以及方向的信号。线性阵列间距，其中为入射信号的波长。阵元数目

等效FIR设计：

通带：，其中

阻带: 其中

使用MATLAB的remez函数设计的FIR系数（也即是个阵元的复共轭系数）为：

是波束形成器的波束图，一般进行取对数，波束图如下图所示。

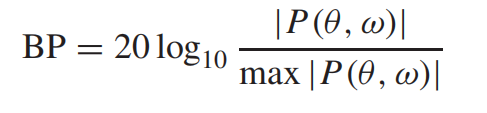
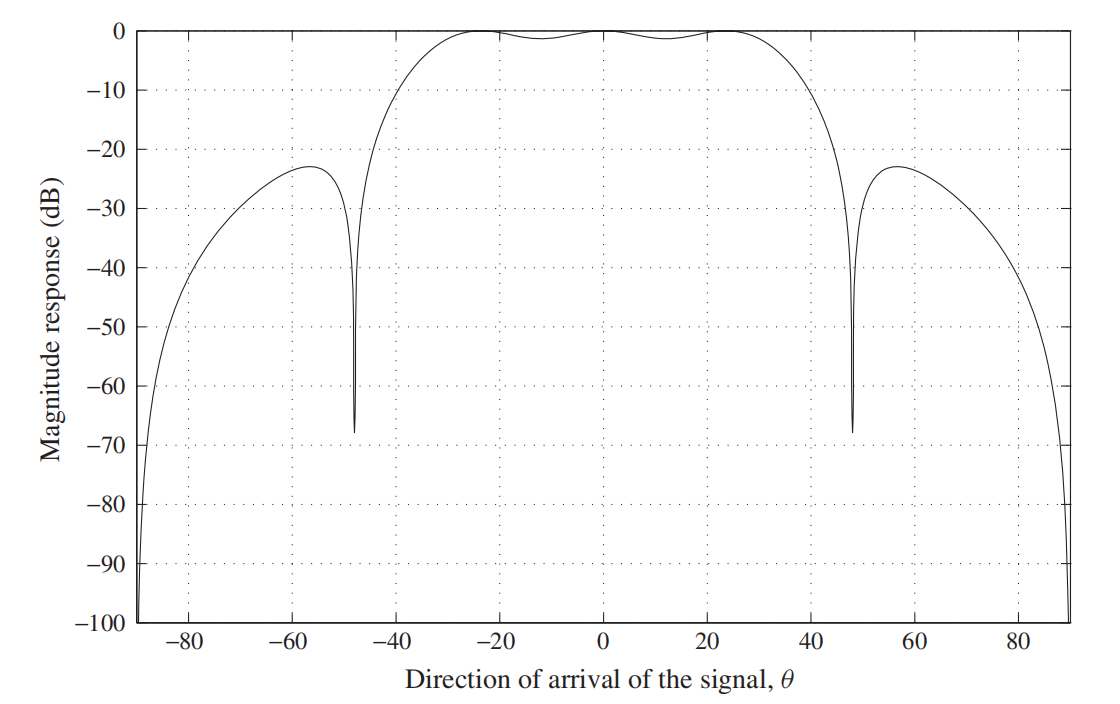
以上的实例是基于阵列的间距等于半波长这个假设，更一般的情况下，令

，

波束响应可写为

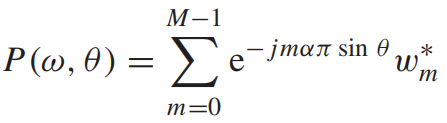
参考：Wei Liu《Wideband Beamforming》University of Sheffifield, UK