目录
插入排序
直接插入排序
希尔排序
希尔排序基本思路解析
希尔排序优化思路解析
完整希尔排序文件
插入排序
直接插入排序
所谓直接插入排序,即每插入一个数据和之前的数据进行大小比较,如果较大放置在后面,较小放置在前面,具体思路分析如下:
//以下面的数组为例
int data[] = { 23,34,84,99,67,26,21,89 };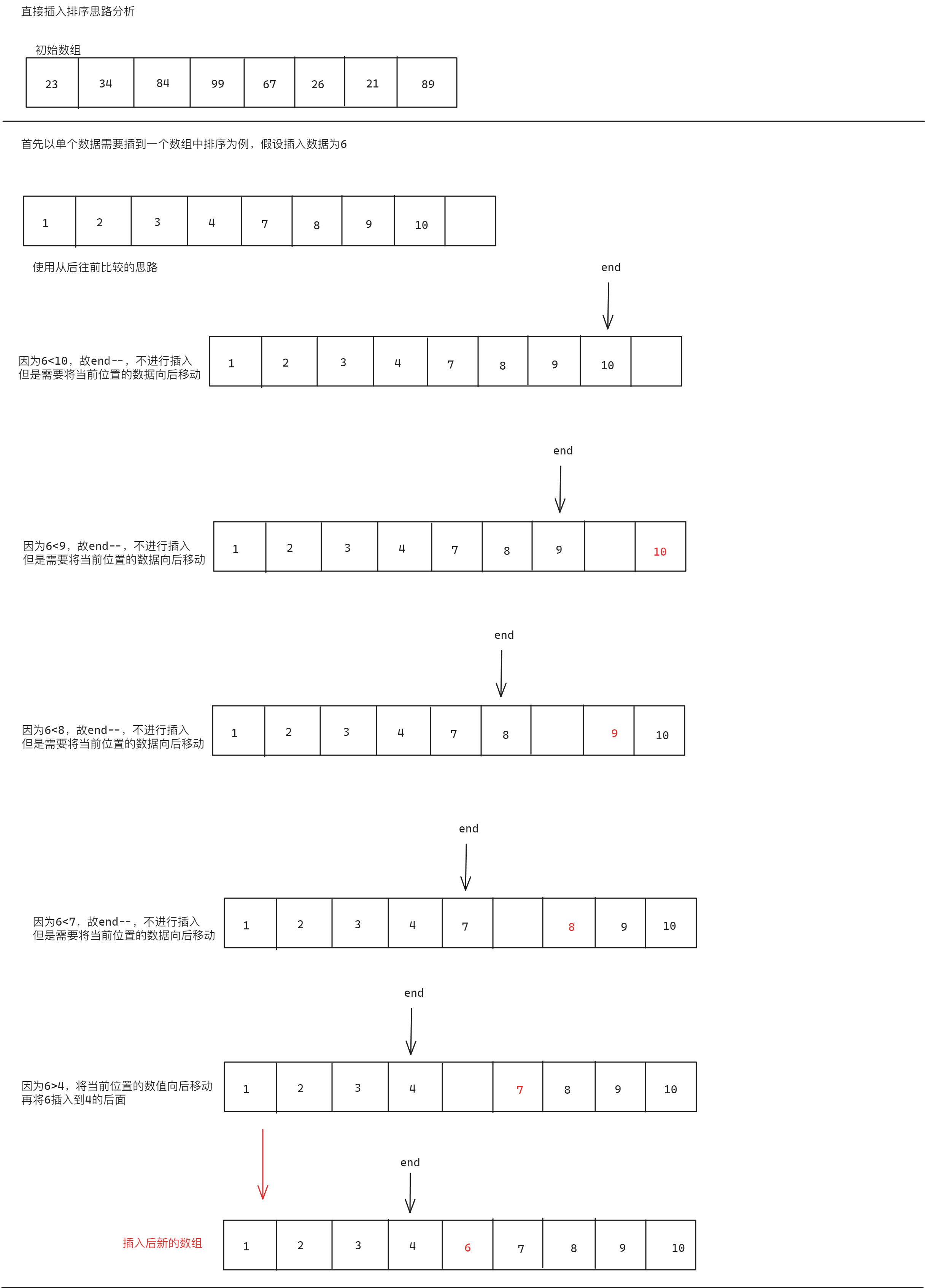
参考代码
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
void DirectInsert_sort(int* data, int sz)
{
// 遍历数组
for (int i = 1; i < sz; i++)
{
int tmp = data[i];//获取数组的当前元素
int end = i - 1;//获取数组的当前元素的上一个元素
//当遇到比tmp大数值时,挪动数据,直到遇到比当前数据小的数据时跳出循环
while (end >= 0)
{
if (data[end] > tmp)
{
data[end + 1] = data[end];
end--;
}
else
{
break;
}
}
//在end的后一个位置插入数据,插入完毕后直接更新i和end继续比较
data[end + 1] = tmp;
}
}
int main()
{
int data[] = { 23,34,84,99,67,26,21,89 };
int sz = sizeof(data) / sizeof(int);
DirectInsert_sort(data, sz);
//打印排序后的数组
for (int i = 0; i < sz; i++)
{
printf("%d ", data[i]);
}
return 0;
}
输出结果:
21 23 26 34 67 84 89 99通过分析可以得出直接插入排序在最坏的情况下(数据为完全逆序的状态)时间复杂度为O(N2),而在最好的情况下(已经为有序状态,只需要遍历一遍数据即可),时间复杂度为O(N)
希尔排序
希尔排序基本思路解析
希尔排序的基本思路是将一组数据按照间隔值gap分成gap组,对各组进行插入排序,这一步被称作预排序,接着再使用直接插入排序对整体再进行一次排序,具体过程如下

//希尔排序基础思路
void ShellSort(int* data, int sz)
{
int gap = 3;
//首先进行三组预排序
for (int i = 0; i < gap; i++)
{
//每一组的排序
for (int j = gap + i; j < sz; j += gap)
{
int end = j - gap;
int tmp = data[j];
while (end >= 0)
{
if (data[end] > tmp)
{
data[end + gap] = data[end];
end -= gap;
}
else
{
break;
}
}
data[end + gap] = tmp;
}
}
//最后进行整体插入排序
gap = 1;
for (int i = gap; i < sz; i += gap)
{
int end = i - 1;
int tmp = data[i];
while (end >= 0)
{
if (data[end] > tmp)
{
data[end + gap] = data[end];
end--;
}
else
{
break;
}
}
data[end + gap] = tmp;
}
}希尔排序优化思路解析
以上思路只是简单的分析,接下来对细节进行分析优化,具体思路如下
首先是间隔值gap,gap决定了分组的数量,也间接决定了最大值走到最后需要的次数,当gap特别大时,最大值很快就会到数据的最末尾,但是同时整体越不接近需要的升序;相反,当gap特别小时,最大值到数据末尾的次数变多,同时整体越接近有序,所以gap数值不容易确定,但是一般取gap为整体的1/3或者取1/2,即gap = size / 3或gap = size / 2 (size是数组长度)
第二个问题,如果将预排序和最后的插入排序分开写,那么需要写五个循环,三层循环解决预排序,两层循环解决最后的插入排序,所以可以考虑将预排序与直接插入排序放在一起,达到在同一个循环中解决问题
可以考虑将每一次循环变量移动的位置改为移动一位,代替原来的一次移动gap位,如下图所示
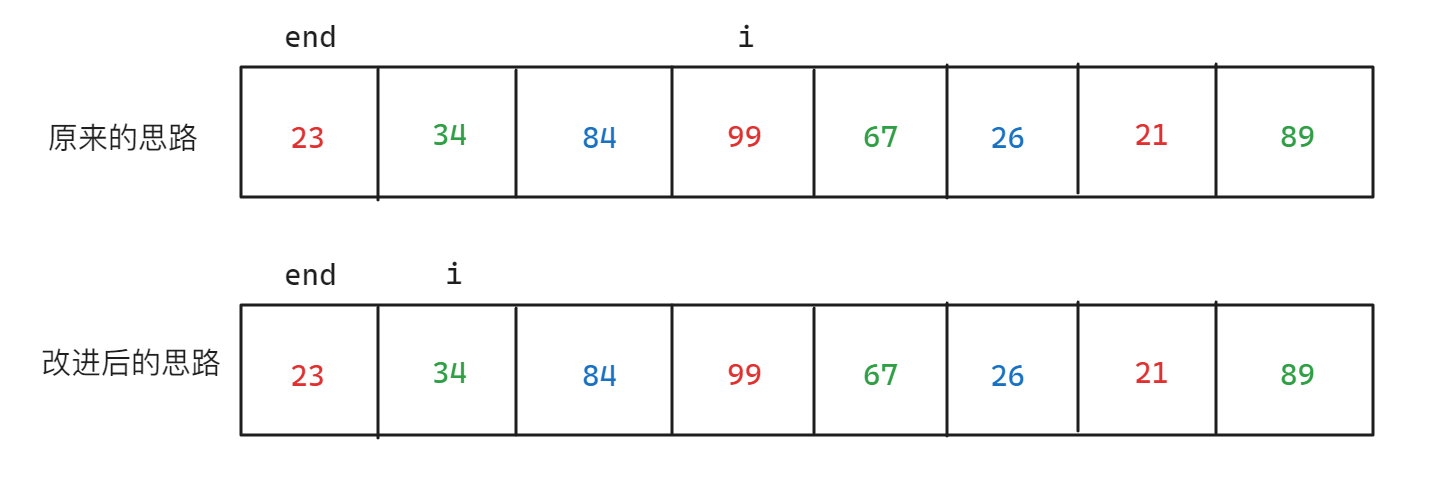
而改进后的思路与原来的思路对比:原来的思路是先排一组,排完一组后再排第二组,而改进后的思路是遇到i当前位置是哪一组的就排哪一组的数据,但是需要注意的是,当前的tmp所在位置为下一个相差gap的位置,该位置需要有确切的数值可以与end进行比较,所以tmp不能越界,假设当前tmp为3,数组最大下标为7,也就是tmp所在的下标最大只能为7,即i + gap不能超过7,故i最大只能为4,所以i不能超过5
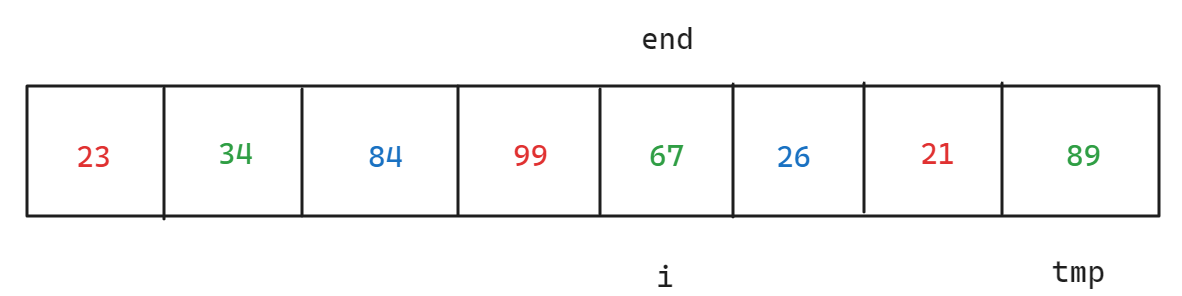
接下来是如何处理预排序和之后的直接排序放在一起的问题,对于这个问题,首先就是gap不能为一个固定值,如果gap为固定的某一个数值,例如3,那么预排序和直接插入排序还是需要两组循环才能解决,鉴于gap最后需要回到1,可以考虑从gap/3分组开始,当预排序完gap为3的一组时,接下来排gap为2的一组,最后着排gap为1的一组,因为第一次gap为3时已经将数据处理了一遍,而gap数值越小,就会使预排序的结果更接近预期的排序结果,所以可以考虑gap = gap / 3,每执行完一次预排序就更换一次gap间隔值,从而达到预排序与最后的直接插入排序放在一起,因为当gap为1时也可以满足预排序的思路,故放在一起也不会有任何冲突,只是间隔值从3变成了1,但是需要注意一个问题,当gap小于3时,gap最后的商为0,导致gap无法取到1,所以需要写成gap = gap / 3 + 1
//希尔排序优化思路
void ShellSort_modified(int* data, int sz)
{
int gap = sz;
while (gap > 1)
{
gap = gap / 3 + 1;// 此处加1是为了确保最后一个gap一定为1,因为最后的直接插入排序是整体各自比较
for (int i = 0; i < sz - gap; i++)
{
int end = i;
int tmp = data[i + gap];
while (end >= 0)
{
if (data[end] > tmp)
{
data[end + gap] = data[end];
end -= gap;
}
else
{
break;
}
}
data[end + gap] = tmp;
}
}
}完整希尔排序文件
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
//希尔排序优化思路
void ShellSort_modified(int* data, int sz)
{
int gap = sz;
while (gap > 1)
{
gap = gap / 3 + 1;// 此处加1是为了确保最后一个gap一定为1,因为最后的直接插入排序是整体各自比较
for (int i = 0; i < sz - gap; i++)
{
int end = i;
int tmp = data[i + gap];
while (end >= 0)
{
if (data[end] > tmp)
{
data[end + gap] = data[end];
end -= gap;
}
else
{
break;
}
}
data[end + gap] = tmp;
}
}
}
int main()
{
int data[] = { 23,34,84,99,67,26,21,89 };
int sz = sizeof(data) / sizeof(int);
ShellSort_modified(data, sz);
for (int i = 0; i < sz; i++)
{
printf("%d ", data[i]);
}
return 0;
}
输出结果:
21 23 26 34 67 84 89 99希尔排序总结:
- 希尔排序是对直接插入排序的优化
- 当
gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比 - 希尔排序的时间复杂度不好计算,因为
gap的取值方法很多,导致很难去计算,因此在好些树中给出的希尔排序的时间复杂度都不固定