本节复习排序中的希尔排序，希尔排序属于插入排序。 希尔排序的代码和插入排序非常类似。 思想却相对于插入排序来说复杂。 

在复习希尔排序之前， 我们需要先复习一下插入排序。

目录

插入排序

插入过程

代码实现

希尔排序

希尔排序的思想

代码实现 

---

插入排序

插入过程

插入排序的思想就是寻找向数组的前面遍历寻找适合的空位。 然后插入进去。 

如图这几个数据。 

插入排序排升序的过程就是：

首先，红指针指向第二个元素。 黑指针指向第一个元素。 然后看黑指针指向的数据是否小于红指针。 小于的话就将红指针的数据放到黑指针的位置。 黑指针所指向以及之后的数据向后覆盖。 如果黑指针越界也没有找到。 那么红指针指向数据就放到第一个位置。 

5放到第一个位置， 9向后覆盖。如图： 

继续：

 红指针向后移动一位。 黑指针继续指向红指针前面的一位。 

 

找不到， 将2放到第一个位置。 5和9向后覆盖如图：

然后红指针重新向后移动一位，黑指针重新指向红指针前一个位置。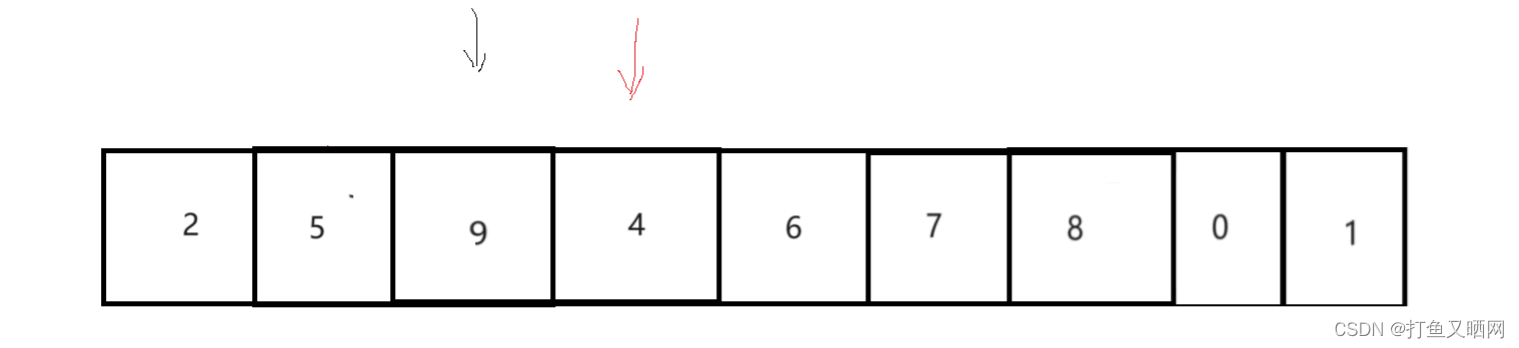

 向前找

找到了， 然后将4放到黑指针指向位置。 2， 5， 9， 向后覆盖： 

然后红指针向后移动一位， 黑指针指向其前一个位置。 循环往复。 这里就不画了。

插入排序就是这么一个过程。 现在我们来实现一下代码： 

代码实现

//插入排序
void InsertSort(int* a, int sz)//插入排序，n^2里面最优的一个 
{
	//[0, end], 有序，插入一个tmp值， 依旧保持串数列有序， 如何插入。 

	for (int i = 1; i < sz; i++) 
	{
		int end = i - 1;//让end指向已有序的最后一个数字。 
		int tmp = a[i];//让将end后面的那个待排序的数字赋值给tmp。

		while (end >= 0) //让end一步一步向后走， 到end == 0位置
		{
			if (tmp < a[end]) //看一下tmp和a[end]哪个比较大， 如果tmp的值小， 那么说明待排序的那个数字应该在第end以前的位置
				//第end个数字以后已排序的数字， 整体向后移动一位。
			{
				a[end + 1] = a[end];//让第end位置的数字向后覆盖一位。
				end--;//end位置的数字向后移动一位的同时， end--， 继续检查下一个数字。 
			}
			else//一直到第tmp 大于 第end位置的数字， 说明tmp应该就是第end + 1位置的数字。 而此时第end + 1和第 end + 2可能
				//是同一个数字或者tmp刚刚开始检查， 没有向后检查呢就检查出错误。
			{
				//为什么不在这里直接进行插入， 是因为可能找到最后一个数也没有找到要排序的位置。
				//那么这一个位置就只能覆盖成别的数字。 
				break;
			}
		}

		a[end + 1] = tmp;//放在这里就解决了到end == 0的时候也没有找到比tmp小的数字的位置。 

	}


}

插入排序实现后理解希尔排序就相对简单一些。 现在来看希尔排序：

希尔排序

希尔排序的思想

希尔排序的思想就是将数组分为几组。 

如图分成三组。 然后对第一组的第一个数和第二组的第一个数和第三组的第一个数进行插入排序。

第一组的第二个数， 第二组的第二个数， 第三组的第三个数进行插入排序

第一组的第三个数， 第二组的第三个数， 第三组的第三个数进行插入排序。

然后分组的大小减小，再次进行这样的排序， 直到每组大小减小到1如图：

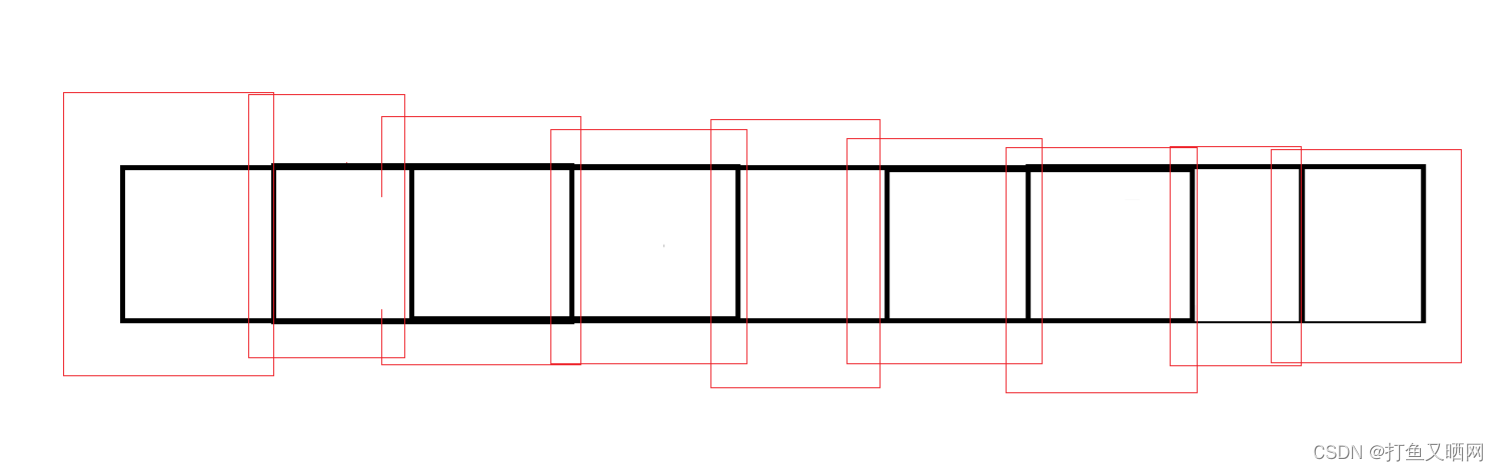
再次进行最后一轮插入排序。 整个数组就成为了有序。 这个过程就是希尔排序。 

代码实现 

//希尔排序
void ShellSort(int* a, int sz) 
{
	int gap = sz / 2;//先让gap为二分之待排序数组长度， 然后每次子插入排序都让gap除以2.

	while (gap > 1) //gap最小为2的时候就能让数组变的有序。 所以gap > 1是为了保证gap会成为最小的那个2.并且不会做多余的排序
	{
		gap = gap / 2;//gap在每次子插入排序中都除以2.
		for (int i = gap; i < sz; i++) //让i 从gap开始， 因为对于一个希尔排序， 每gap个数字可以看成一个数字。 
			//因为每组内对应位置的数字都会和其他gap组合内的其他数字进行子插入排序。 
		{
			int end = i - gap;//gap为一组， gap看成一个数字。
			int tmp = a[end + gap];//gap为一组， gap看成一个数字，
			//例如， 第一个gap内第一个数字和第二个gap内第一个数字会进行插入排序。
			while (end >= 0) 
			{
				if (tmp < a[end]) //这里不好想像， 其实就是寻找一个合适的待排序的数字的位置。 这个数字碰到比他大的
					//end就向前移动一位。 然后和前一个数字比较。
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else 
				{
					break;
				}
			}
			a[end + gap] = tmp;//这里和插入排序相同

		}
	}
}