目录
一、引入
二、分类
三、列表
1. C语言中数组的存储方式
2. Python中列表的存储方式
四、栈
1. 栈的应用 -- 括号匹配问题
一、引入
- 定义:数据结构是指相互之间存在着一种或多种关系的数据元素的集合和该集合中数据元素之间的关系组成。
- 简单来说,书记结果就是设计数据以何种方式组织并存储在计算机中。
- 比如:列表、集合与字典等都是一种数据结构。
- N.Wirth:‘“程序 = 数据结构 + 算法”
二、分类
数据结构按照其逻辑结构可分为线性结构、树结构、图结构。
- 线性结构:数据结构中的元素存在一对一的相互关系(比如列表)。
- 树结构:数据结构中的元素存在一对多的相互关系。(二叉树)
- 图结构:数据结构中的元素存在多对多的相互关系。(地图)
三、列表
列表中的元素按照顺序存储。
1. C语言中数组的存储方式
C语言中的数组需要指定数组的大小。
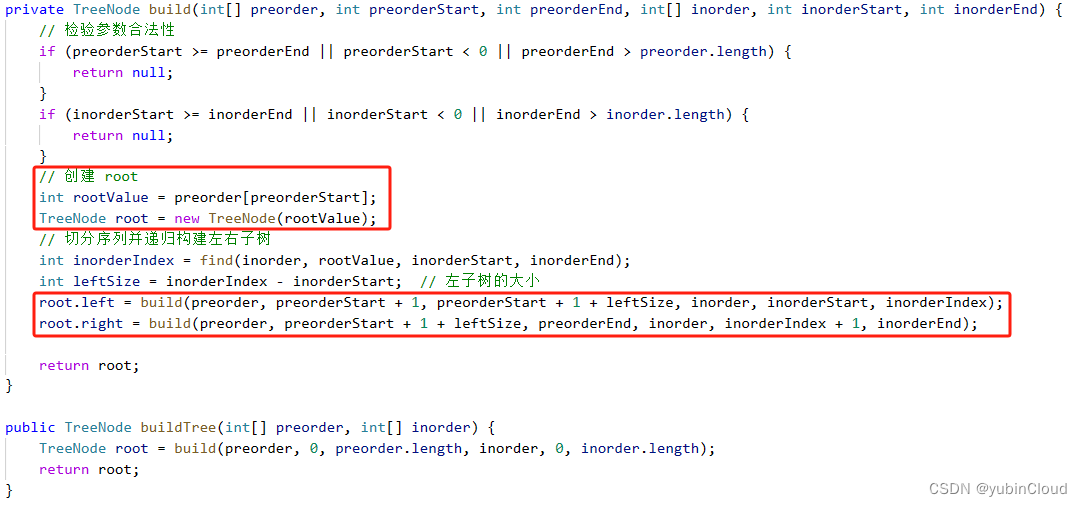
例如一个数组存整数,假如在32位机器上存放。
假如我们需要查找a[2],则a[2] : 100 +2 * 4 = 108 ,根据位置取出对应的元素。
数组与列表的区别:
- 数组元素类型要相同
- 数组长度固定
2. Python中列表的存储方式
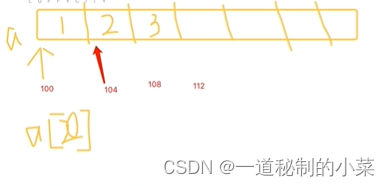
Pyhton中列表存放的是对应的数据的地址。
32位机器上,一个整数占4个字节,一个地址也占4个字节;64位机器上,一个整数占8个字节。
查找元素的复杂度为O(1)。
插入和删除对于列表来说都是O(n)的复杂度。
删除元素后,后面的数据所对应的地址会向前补;插入元素,后面的元素向后面挪动。
四、栈
定义:栈是一个数据集合,可以理解为只能在一端进行插入或删除操作的列表。
特点:后进后出LIFO(last-in, first-out)
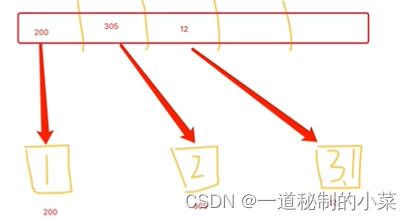
栈的概念:栈顶、栈底
栈的基本操作:
- 进栈(压栈):push(相当于最上面再放一本书)
- 出栈:pop(相当于取出最上面的一本书)
- 取栈顶:gettop (查看最上面的元素的信息,但是不拿走)
我们可以创建一个class,来实现栈的功能,示例代码如下所示:
class Stack:
def __init__(self):
self.stack = []
def push(self, element): # 进栈存放元素
self.stack.append(element)
def pop(self): # 出栈取元素
return self.stack.pop()
def get_top(self): # 返回栈顶元素
if len(self.stack) > 0:
return self.stack[-1]
else:
return None或者我们可以直接使用一般的列表结构即可实现栈:
- 进栈: li.append
- 出栈:li.pop
- 取栈顶:li[-1]
1. 栈的应用 -- 括号匹配问题
括号匹配问题:给一个字符串,其中包含小括号、中括号、大括号,求该字符串中的括号是否匹配。
例如:
- ()()[][] 匹配
- ([{()}]) 匹配
- []( 不匹配
- [(]) 不匹配
示例代码如下所示:
class Stack:
def __init__(self):
self.stack = []
def push(self, element): # 进栈存放元素
self.stack.append(element)
def pop(self): # 出栈取元素
return self.stack.pop()
def get_top(self): # 返回栈顶元素
if len(self.stack) > 0:
return self.stack[-1]
else:
return None
def is_empty(self):
return len(self.stack) == 0
def brace_match(s):
stack = Stack()
match = {'}':'{', ')':'(', ']':'['}
for ch in s:
if ch in {'(', '[', '{'}: # ch是左括号
stack.push(ch)
else: # ch为右括号
if stack.is_empty(): # 如果此时栈为空,也就是第一个字符不是左括号
return False
elif stack.get_top() == match[ch]: # 取出栈顶元素,是否与match匹配
stack.pop() # 取出最后面一个与之相对于的左括号的元素
else: #不匹配
return False
if stack.is_empty():
return True
else:
return False