程序员常用的几种算法
- 一、程序员算法汇总
- 二、程序员常用的几种算法
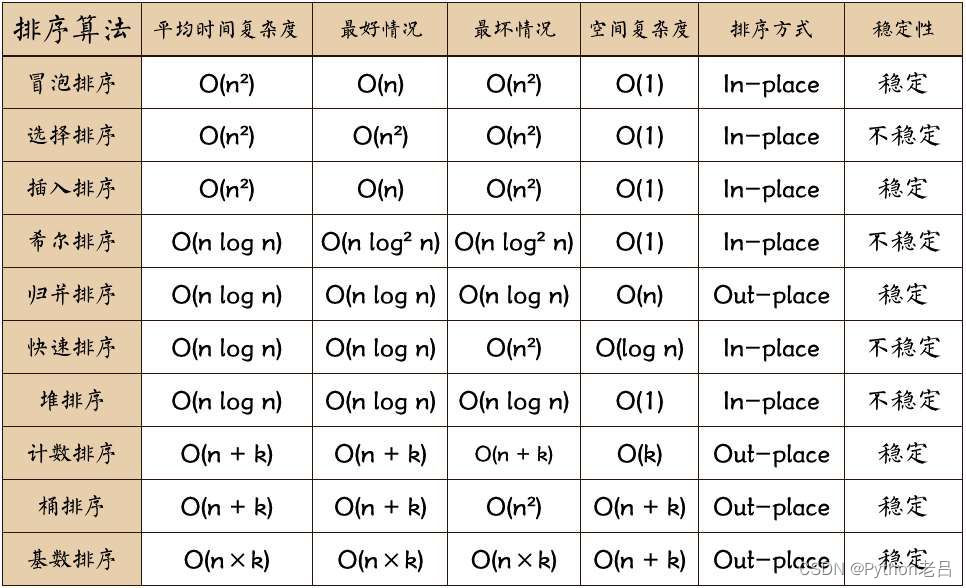
- 1.选择排序算法
- 1.1 选择排序算法解析:
- 1.2 示例代码:
- 2.插入排序算法
- 2.1 插入排序算法解析:
- 2.2 示例代码:
- 3.冒泡排序算法
- 3.1 冒泡排序算法解析:
- 3.2 示例代码:
- 3.3 优化冒泡排序算法
- 4.希尔排序算法
- 4.1 希尔排序算法解析:
- 4.2 示例代码:
- 5.归并排序算法
- 5.1 归并排序算法解析:
- 5.2 示例代码:
- 6.快速排序算法
- 6.1 快速排序算法解析:
- 6.2 示例代码:
- 7.堆排序算法
- 7.1 堆排序算法解析:
- 7.2 示例代码:
- 8.计数排序算法
- 8.1 计数排序算法解析:
- 8.2 示例代码:
- 8.3 优化计数排序代码
- 9.桶排序算法
- 9.1 桶排序算法解析:
- 9.2 示例代码:
- 10.基数排序算法
- 10.1 基数排序算法解析:
- 10.2 示例代码:
- 总结
一、程序员算法汇总
- 线性搜索算法:通过逐个比较来查找给定值。
- 二分搜索算法:通过将搜索区间减半来快速查找有序数组中的元素。
- 插入排序算法:通过逐个地插入元素来对数组进行排序。
- 选择排序算法:通过选择最小(或最大)的元素来对数组进行排序。
- 冒泡排序算法:通过相邻元素的比较和交换来对数组进行排序。
- 归并排序算法:通过将数组分成较小的块并逐步合并它们来对数组进行排序。
- 快速排序算法:通过选择一个基准元素并将数组分成两个子数组来对数组进行排序。
- 堆排序算法:通过构建最大(或最小)堆来对数组进行排序。
- 计数排序算法:通过计算元素的出现次数来对数组进行排序。
- 桶排序算法:通过将元素分配到不同的桶中来对数组进行排序。
- 基数排序算法:通过将元素按照位数进行排序来对数组进行排序。
- 字符串匹配算法:通过查找模式在给定文本中的出现位置来进行字符串匹配。
- 广度优先搜索算法:通过遍历节点的邻居来搜索图的最短路径。
- 深度优先搜索算法:通过递归地遍历节点的邻居来搜索图的最短路径。
- Dijkstra算法:通过计算节点之间的最短路径来搜索加权图。
- Floyd-Warshall算法:通过计算所有节点之间的最短路径来搜索加权图。
- 贝尔曼-福特算法:通过计算从源节点到所有其他节点的最短路径来搜索加权图。
- A*算法:通过启发式函数来搜索图的最短路径。
- 拓扑排序算法:通过确定图中节点之间的依赖关系来排序图的节点。
- Kruskal算法:通过选择边来构建最小生成树。
- Prim算法:通过选择节点来构建最小生成树。
- 最大流算法:通过在网络中查找最大流量路径来解决最大流问题。
- 最小割算法:通过在网络中查找最小割来解决最小割问题。
- 背包问题算法:通过动态规划来解决背包问题。
- 最长公共子序列算法:通过动态规划来查找两个序列的最长公共子序列。
- 最短公共超序列算法:通过动态规划来查找两个序列的最短公共超序列。
- 最长递增子序列算法:通过动态规划来查找给定序列的最长递增子序列。
- 最大子数组和算法:通过动态规划来查找给定数组的最大子数组和。
- 最优二叉搜索树算法:通过动态规划来构建最优二叉搜索树。
- 多重背包问题算法:通过动态规划来解决多重背包问题。
- 最大公约数算法:通过欧几里得算法来查找两个数的最大公约数。
- 最小公倍数算法:通过最大公约数算法来计算两个数的最小公倍数。
- 斐波那契数列算法:通过递归或动态规划来生成斐波那契数列。
- 快速幂算法:通过递归或迭代来计算幂。
- 回溯算法:通过尝试所有可能的解决方案来解决组合优化问题。
二、程序员常用的几种算法
1.选择排序算法
1.1 选择排序算法解析:
先找到数组中最小的那个元素,之后将它和数组的第一个元素交换位置(如果第一个元素就是最小元素那么它就和自己交换)。在之后在剩下的元素中找到最小的元素,将它与数组的第二个元素交换位置。如此往复,直到将整个数组排序。这种方法我们称之为选择排序。
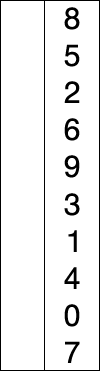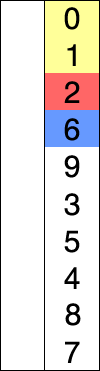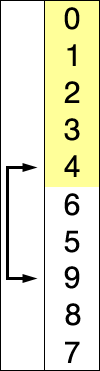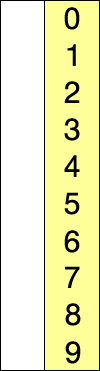
1.2 示例代码:
public class SelectSort {
public static int[] selectSort(int[] a) {
int n = a.length;
for (int i = 0; i < n - 1; i++) {
int min = i;
for (int j = i + 1; j < n; j++) {
if(a[min] > a[j]) min = j;
}
//交换
int temp = a[i];
a[i] = a[min];
a[min] = temp;
}
return a;
}
}
2.插入排序算法
2.1 插入排序算法解析:
我们在玩打牌的时候,你是怎么整理那些牌的呢?一种简单的方法就是一张一张的来,将每一张牌插入到其他已经有序的牌中的适当位置。当我们给无序数组做排序的时候,为了要插入元素,我们需要腾出空间,将其余所有元素在插入之前都向右移动一位,这种算法我们称之为插入排序。
过程简单描述:
1、从数组第2个元素开始抽取元素。
2、把它与左边第一个元素比较,如果左边第一个元素比它大,则继续与左边第二个元素比较下去,直到遇到不比它大的元素,然后插到这个元素的右边。
3、继续选取第3,4,….n个元素,重复步骤 2 ,选择适当的位置插入。
2.2 示例代码:
public class InsertSort {
public static int[] insertSort(int[] arr) {
if(arr == null || arr.length < 2)
return arr;
int n = arr.length;
for (int i = 1; i < n; i++) {
int temp = arr[i];
int k = i - 1;
while(k >= 0 && arr[k] > temp)
k--;
//腾出位置插进去,要插的位置是 k + 1;
for(int j = i ; j > k + 1; j--)
arr[j] = arr[j-1];
//插进去
arr[k+1] = temp;
}
return arr;
}
}
3.冒泡排序算法
3.1 冒泡排序算法解析:
把第一个元素与第二个元素比较,如果第一个比第二个大,则交换他们的位置。接着继续比较第二个与第三个元素,如果第二个比第三个大,则交换他们的位置….
我们对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样一趟比较交换下来之后,排在最右的元素就会是最大的数。除去最右的元素,我们对剩余的元素做同样的工作,如此重复下去,直到排序完成。
3.2 示例代码:
public class BubbleSort {
public static int[] bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return arr;
}
int n = arr.length;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n -i - 1; j++) {
if (arr[j + 1] < arr[j]) {
int t = arr[j];
arr[j] = arr[j+1];
arr[j+1] = t;
}
}
}
return arr;
}
)
3.3 优化冒泡排序算法
假如从开始的第一对到结尾的最后一对,相邻的元素之间都没有发生交换的操作,这意味着右边的元素总是大于等于左边的元素,此时的数组已经是有序的了,我们无需再对剩余的元素重复比较下去了。
public class BubbleSort {
public static int[] bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return arr;
}
int n = arr.length;
for (int i = 0; i < n; i++) {
boolean flag = true;
for (int j = 0; j < n -i - 1; j++) {
if (arr[j + 1] < arr[j]) {
flag = false;
int t = arr[j];
arr[j] = arr[j+1];
arr[j+1] = t;
}
}
//一趟下来是否发生位置交换
if(false)
break;
}
return arr;
}
}
4.希尔排序算法
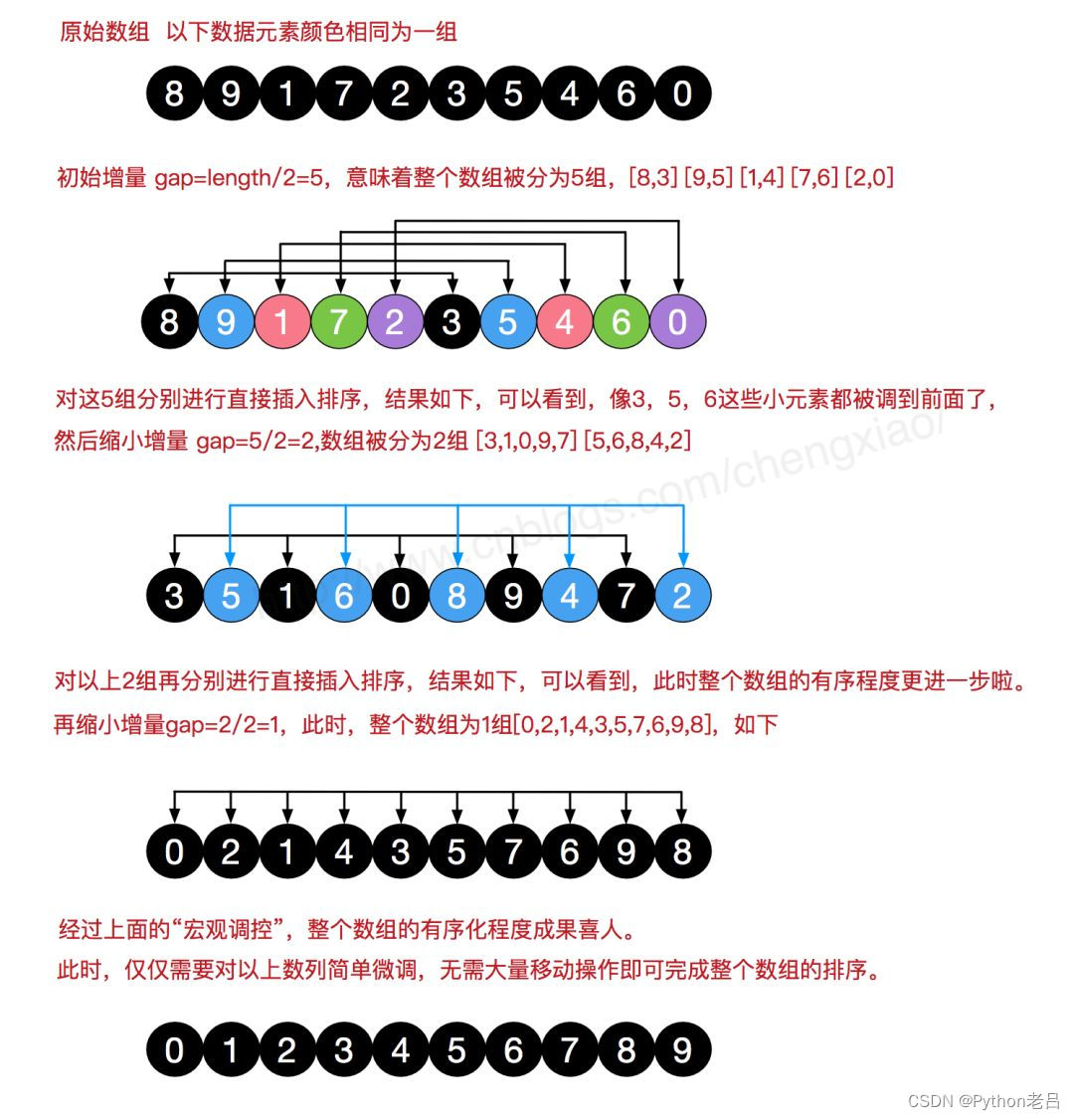
4.1 希尔排序算法解析:
希尔排序可以说是插入排序的一种变种。无论是插入排序还是冒泡排序,如果数组的最大值刚好是在第一位,要将它挪到正确的位置就需要 n - 1 次移动。也就是说,原数组的一个元素如果距离它正确的位置很远的话,则需要与相邻元素交换很多次才能到达正确的位置,这样是相对比较花时间了。
希尔排序就是为了加快速度简单地改进了插入排序,交换不相邻的元素以对数组的局部进行排序。
希尔排序的思想是采用插入排序的方法,先让数组中任意间隔为 h 的元素有序,刚开始 h 的大小可以是 h = n / 2,接着让 h = n / 4,让 h 一直缩小,当 h = 1 时,也就是此时数组中任意间隔为1的元素有序,此时的数组就是有序的了。
4.2 示例代码:
public class ShellSort {
public static int[] shellSort(int arr[]) {
if (arr == null || arr.length < 2) return arr;
int n = arr.length;
// 对每组间隔为 h的分组进行排序,刚开始 h = n / 2;
for (int h = n / 2; h > 0; h /= 2) {
//对各个局部分组进行插入排序
for (int i = h; i < n; i++) {
// 将arr[i] 插入到所在分组的正确位置上
insertI(arr, h, i);
}
}
return arr;
}
/**
* 将arr[i]插入到所在分组的正确位置上
* arr[i]] 所在的分组为 ... arr[i-2*h],arr[i-h], arr[i+h] ...
*/
private static void insertI(int[] arr, int h, int i) {
int temp = arr[i];
int k;
for (k = i - h; k > 0 && temp < arr[k]; k -= h) {
arr[k + h] = arr[k];
}
arr[k + h] = temp;
}
}
需要注意的是,对各个分组进行插入的时候并不是先对一个组排序完了再来对另一个组排序,而是轮流对每个组进行排序。
5.归并排序算法
5.1 归并排序算法解析:
将一个大的无序数组有序,我们可以把大的数组分成两个,然后对这两个数组分别进行排序,之后在把这两个数组合并成一个有序的数组。由于两个小的数组都是有序的,所以在合并的时候是很快的。
通过递归的方式将大的数组一直分割,直到数组的大小为 1,此时只有一个元素,那么该数组就是有序的了,之后再把两个数组大小为1的合并成一个大小为2的,再把两个大小为2的合并成4的 …… 直到全部小的数组合并起来。
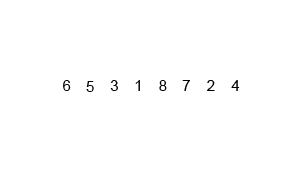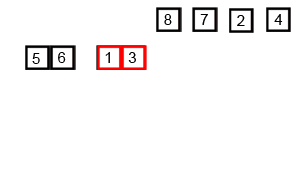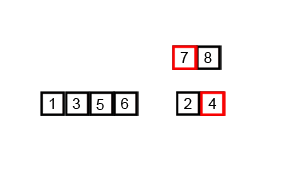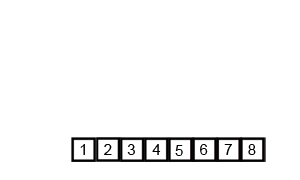
5.2 示例代码:
public class MergeSort {
// 归并排序
public static int[] mergeSort(int[] arr, int left, int right) {
// 如果 left == right,表示数组只有一个元素,则不用递归排序
if (left < right) {
// 把大的数组分隔成两个数组
int mid = (left + right) / 2;
// 对左半部分进行排序
arr = mergeSort(arr, left, mid);
// 对右半部分进行排序
arr = mergeSort(arr, mid + 1, right);
//进行合并
merge(arr, left, mid, right);
}
return arr;
}
// 合并函数,把两个有序的数组合并起来
// arr[left..mif]表示一个数组,arr[mid+1 .. right]表示一个数组
private static void merge(int[] arr, int left, int mid, int right) {
//先用一个临时数组把他们合并汇总起来
int[] a = new int[right - left + 1];
int i = left;
int j = mid + 1;
int k = 0;
while (i <= mid && j <= right) {
if (arr[i] < arr[j]) {
a[k++] = arr[i++];
} else {
a[k++] = arr[j++];
}
}
while(i <= mid) a[k++] = arr[i++];
while(j <= right) a[k++] = arr[j++];
// 把临时数组复制到原数组
for (i = 0; i < k; i++) {
arr[left++] = a[i];
}
}
}
然而面试官要你写个非递归式的归并排序怎么办?
别怕,我这还撸了个非递归式的归并排序,代码如下:
public class MergeSort {
// 非递归式的归并排序
public static int[] mergeSort(int[] arr) {
int n = arr.length;
// 子数组的大小分别为1,2,4,8...
// 刚开始合并的数组大小是1,接着是2,接着4....
for (int i = 1; i < n; i += i) {
//进行数组进行划分
int left = 0;
int mid = left + i - 1;
int right = mid + i;
//进行合并,对数组大小为 i 的数组进行两两合并
while (right < n) {
// 合并函数和递归式的合并函数一样
merge(arr, left, mid, right);
left = right + 1;
mid = left + i - 1;
right = mid + i;
}
// 还有一些被遗漏的数组没合并,千万别忘了
// 因为不可能每个字数组的大小都刚好为 i
if (left < n && mid < n) {
merge(arr, left, mid, n - 1);
}
}
return arr;
}
}
6.快速排序算法
6.1 快速排序算法解析:
我们从数组中选择一个元素,我们把这个元素称之为中轴元素吧,然后把数组中所有小于中轴元素的元素放在其左边,所有大于或等于中轴元素的元素放在其右边,显然,此时中轴元素所处的位置的是有序的。也就是说,我们无需再移动中轴元素的位置。
从中轴元素那里开始把大的数组切割成两个小的数组(两个数组都不包含中轴元素),接着我们通过递归的方式,让中轴元素左边的数组和右边的数组也重复同样的操作,直到数组的大小为1,此时每个元素都处于有序的位置。
6.2 示例代码:
public class QuickSort {
public static int[] quickSort(int[] arr, int left, int right) {
if (left < right) {
//获取中轴元素所处的位置
int mid = partition(arr, left, right);
//进行分割
arr = quickSort(arr, left, mid - 1);
arr = quickSort(arr, mid + 1, right);
}
return arr;
}
private static int partition(int[] arr, int left, int right) {
//选取中轴元素
int pivot = arr[left];
int i = left + 1;
int j = right;
while (true) {
// 向右找到第一个小于等于 pivot 的元素位置
while (i <= j && arr[i] <= pivot) i++;
// 向左找到第一个大于等于 pivot 的元素位置
while(i <= j && arr[j] >= pivot ) j--;
if(i >= j)
break;
//交换两个元素的位置,使得左边的元素不大于pivot,右边的不小于pivot
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
arr[left] = arr[j];
// 使中轴元素处于有序的位置
arr[j] = pivot;
return j;
}
}
7.堆排序算法
7.1 堆排序算法解析:
堆的特点就是堆顶的元素是一个最值,大顶堆的堆顶是最大值,小顶堆则是最小值。
堆排序就是把堆顶的元素与最后一个元素交换,交换之后破坏了堆的特性,我们再把堆中剩余的元素再次构成一个大顶堆,然后再把堆顶元素与最后第二个元素交换….如此往复下去,等到剩余的元素只有一个的时候,此时的数组就是有序的了。

7.2 示例代码:
public class Head {
// 堆排序
public static int[] headSort(int[] arr) {
int n = arr.length;
//构建大顶堆
for (int i = (n - 2) / 2; i >= 0; i--) {
downAdjust(arr, i, n - 1);
}
//进行堆排序
for (int i = n - 1; i >= 1; i--) {
// 把堆顶元素与最后一个元素交换
int temp = arr[i];
arr[i] = arr[0];
arr[0] = temp;
// 把打乱的堆进行调整,恢复堆的特性
downAdjust(arr, 0, i - 1);
}
return arr;
}
//下沉操作
public static void downAdjust(int[] arr, int parent, int n) {
//临时保存要下沉的元素
int temp = arr[parent];
//定位左孩子节点的位置
int child = 2 * parent + 1;
//开始下沉
while (child <= n) {
// 如果右孩子节点比左孩子大,则定位到右孩子
if(child + 1 <= n && arr[child] < arr[child + 1])
child++;
// 如果孩子节点小于或等于父节点,则下沉结束
if (arr[child] <= temp ) break;
// 父节点进行下沉
arr[parent] = arr[child];
parent = child;
child = 2 * parent + 1;
}
arr[parent] = temp;
}
}
8.计数排序算法
8.1 计数排序算法解析:
计数排序是一种适合于最大值和最小值的差值不是不是很大的排序。
基本思想:就是把数组元素作为数组的下标,然后用一个临时数组统计该元素出现的次数,例如 temp[i] = m, 表示元素 i 一共出现了 m 次。最后再把临时数组统计的数据从小到大汇总起来,此时汇总起来是数据是有序的。
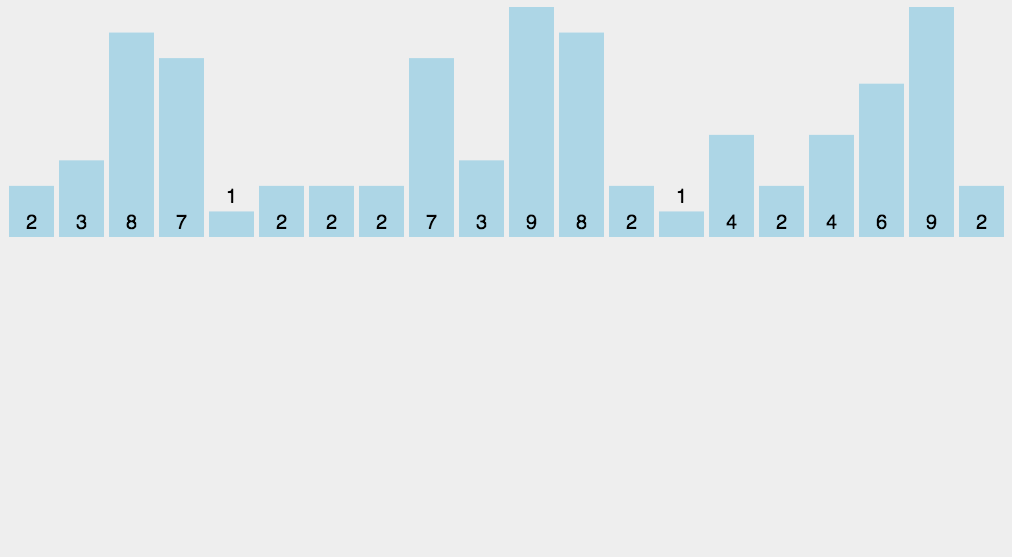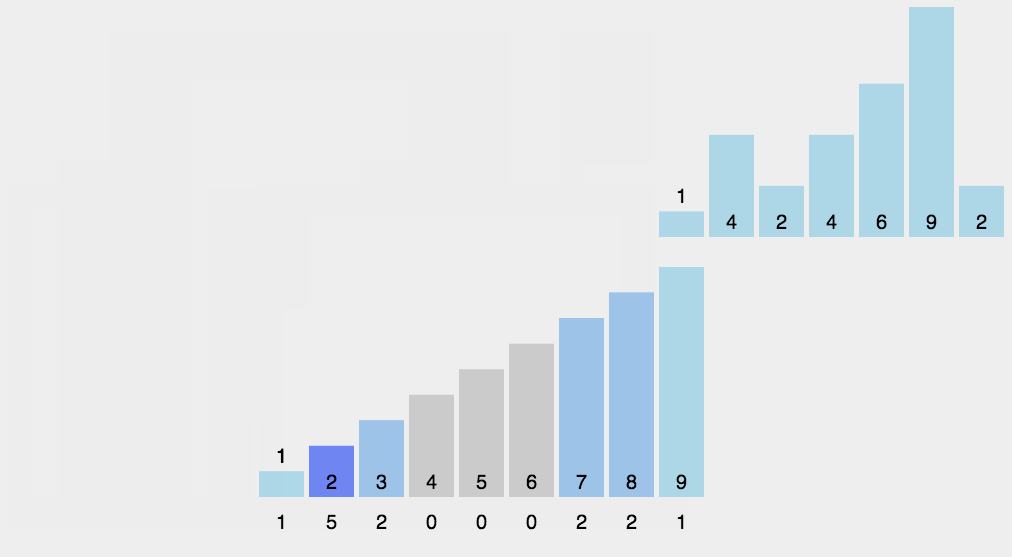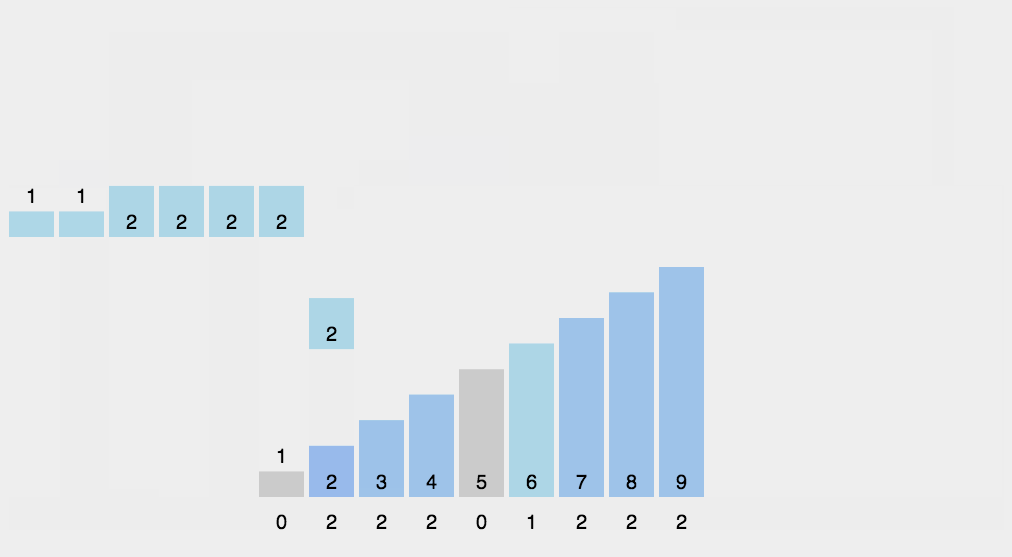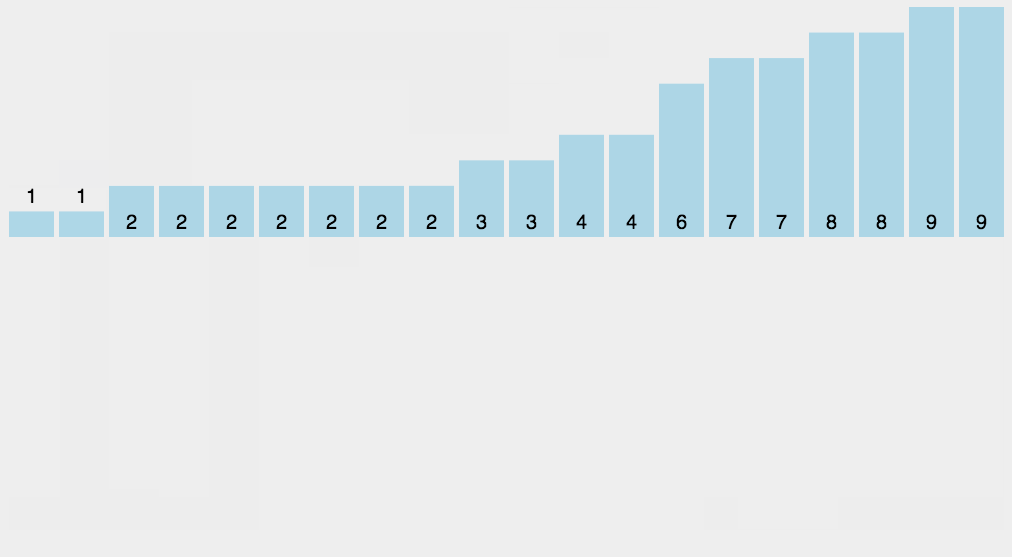
8.2 示例代码:
public class Counting {
public static int[] countSort(int[] arr) {
if(arr == null || arr.length < 2) return arr;
int n = arr.length;
int max = arr[0];
// 寻找数组的最大值
for (int i = 1; i < n; i++) {
if(max < arr[i])
max = arr[i];
}
//创建大小为max的临时数组
int[] temp = new int[max + 1];
//统计元素i出现的次数
for (int i = 0; i < n; i++) {
temp[arr[i]]++;
}
int k = 0;
//把临时数组统计好的数据汇总到原数组
for (int i = 0; i <= max; i++) {
for (int j = temp[i]; j > 0; j--) {
arr[k++] = i;
}
}
return arr;
}
}
8.3 优化计数排序代码
上面的代码中,我们是根据 max 的大小来创建对应大小的数组,假如原数组只有10个元素,并且最小值为 min = 10000,最大值为 max = 10005,那我们创建 10005 + 1 大小的数组不是很吃亏,最大值与最小值的差值为 5,所以我们创建大小为6的临时数组就可以了。
也就是说,我们创建的临时数组大小 (max - min + 1)就可以了,然后在把 min作为偏移量。优化之后的代码如下所示:
public class Counting {
public static int[] sort(int[] arr) {
if(arr == null || arr.length < 2) return arr;
int n = arr.length;
int min = arr[0];
int max = arr[0];
// 寻找数组的最大值与最小值
for (int i = 1; i < n; i++) {
if(max < arr[i])
max = arr[i];
if(min > arr[i])
min = arr[i];
}
int d = max - min + 1;
//创建大小为max的临时数组
int[] temp = new int[d];
//统计元素i出现的次数
for (int i = 0; i < n; i++) {
temp[arr[i] - min]++;
}
int k = 0;
//把临时数组统计好的数据汇总到原数组
for (int i = 0; i < d; i++) {
for (int j = temp[i]; j > 0; j--) {
arr[k++] = i + min;
}
}
return arr;
}
}
9.桶排序算法
9.1 桶排序算法解析:
桶排序就是把最大值和最小值之间的数进行瓜分,例如分成 10 个区间,10个区间对应10个桶,我们把各元素放到对应区间的桶中去,再对每个桶中的数进行排序,可以采用归并排序,也可以采用快速排序之类的,之后每个桶里面的数据就是有序的了,我们在进行合并汇总。
9.2 示例代码:
public class BucketSort {
public static int[] BucketSort(int[] arr) {
if(arr == null || arr.length < 2) return arr;
int n = arr.length;
int max = arr[0];
int min = arr[0];
// 寻找数组的最大值与最小值
for (int i = 1; i < n; i++) {
if(min > arr[i])
min = arr[i];
if(max < arr[i])
max = arr[i];
}
//和优化版本的计数排序一样,弄一个大小为 min 的偏移值
int d = max - min;
//创建 d / 5 + 1 个桶,第 i 桶存放 5*i ~ 5*i+5-1范围的数
int bucketNum = d / 5 + 1;
ArrayList<LinkedList<Integer>> bucketList = new ArrayList<>(bucketNum);
//初始化桶
for (int i = 0; i < bucketNum; i++) {
bucketList.add(new LinkedList<Integer>());
}
//遍历原数组,将每个元素放入桶中
for (int i = 0; i < n; i++) {
bucketList.get((arr[i]-min)/d).add(arr[i] - min);
}
//对桶内的元素进行排序,我这里采用系统自带的排序工具
for (int i = 0; i < bucketNum; i++) {
Collections.sort(bucketList.get(i));
}
//把每个桶排序好的数据进行合并汇总放回原数组
int k = 0;
for (int i = 0; i < bucketNum; i++) {
for (Integer t : bucketList.get(i)) {
arr[k++] = t + min;
}
}
return arr;
}
}
10.基数排序算法
10.1 基数排序算法解析:
基数排序的排序思路是这样的:先以个位数的大小来对数据进行排序,接着以十位数的大小来多数进行排序,接着以百位数的大小……排到最后,就是一组有序的元素了。不过,他在以某位数进行排序的时候,是用“桶”来排序的。由于某位数(个位/十位….,不是一整个数)的大小范围为0-9,所以我们需要10个桶,然后把具有相同数值的数放进同一个桶里,之后再把桶里的数按照0号桶到9号桶的顺序取出来,这样一趟下来,按照某位数的排序就完成了

10.2 示例代码:
public class RadioSort {
public static int[] radioSort(int[] arr) {
if(arr == null || arr.length < 2) return arr;
int n = arr.length;
int max = arr[0];
// 找出最大值
for (int i = 1; i < n; i++) {
if(max < arr[i]) max = arr[i];
}
// 计算最大值是几位数
int num = 1;
while (max / 10 > 0) {
num++;
max = max / 10;
}
// 创建10个桶
ArrayList<LinkedList<Integer>> bucketList = new ArrayList<>(10);
//初始化桶
for (int i = 0; i < 10; i++) {
bucketList.add(new LinkedList<Integer>());
}
// 进行每一趟的排序,从个位数开始排
for (int i = 1; i <= num; i++) {
for (int j = 0; j < n; j++) {
// 获取每个数最后第 i 位是数组
int radio = (arr[j] / (int)Math.pow(10,i-1)) % 10;
//放进对应的桶里
bucketList.get(radio).add(arr[j]);
}
//合并放回原数组
int k = 0;
for (int j = 0; j < 10; j++) {
for (Integer t : bucketList.get(j)) {
arr[k++] = t;
}
//取出来合并了之后把桶清光数据
bucketList.get(j).clear();
}
}
return arr;
}
}
总结
编程算法是编程世界的核心,它们可以解决各种问题。从搜索和排序到图算法和动态规划,每种算法都有其独特的应用场景。通过掌握这些算法,您将能够更好地理解编程世界的奥秘,并且能够更高效地解决问题。无论您是新手还是有经验的程序员,学习和掌握这些算法都是必不可少的。希望本文对您有所帮助,并能够激发您在编程领域的创造力和热情。
如若本文能帮您, 希望您能关注Python老吕的CSDN博客 ;
您可以在本文进行评论,老吕将努力快速回复,和您近距离交流各种问题;
博主ID:Python老吕,希望大家点赞、评论、收藏。