超级简单的Docker安装(centos7)
news2026/2/15 13:45:32
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1500891.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
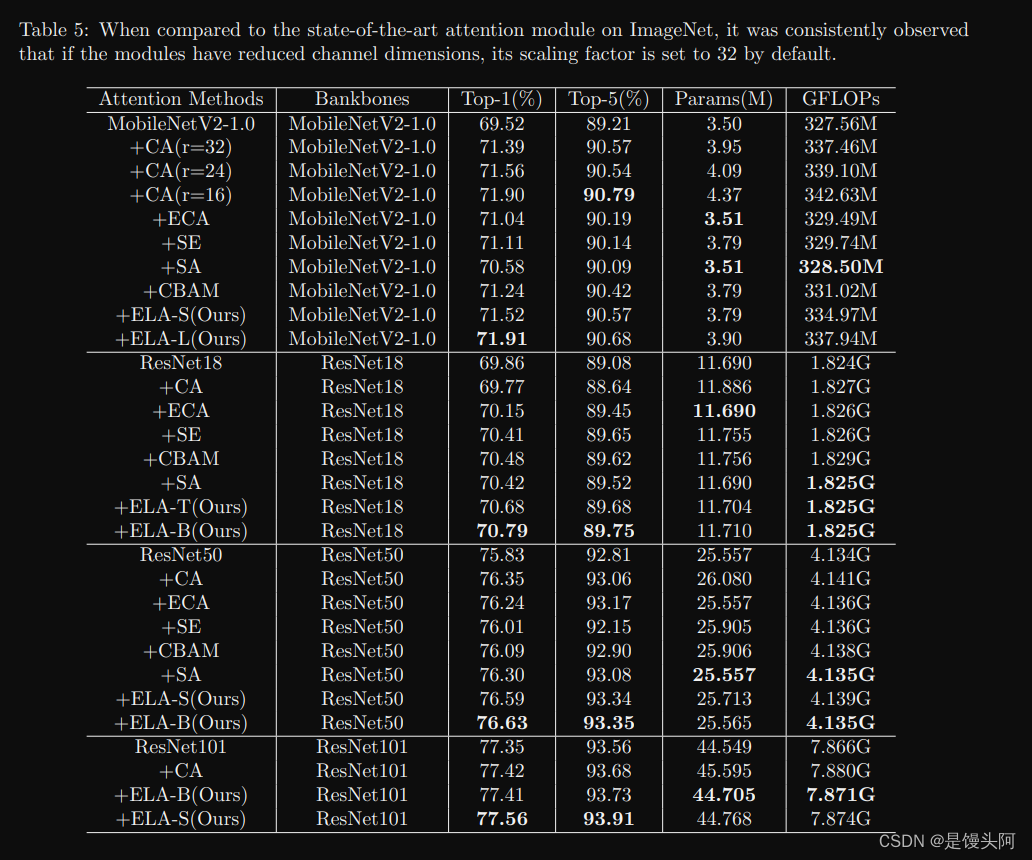
48、兰州大学、青海师范:专门用于深度CNNs的天阶斗技-ELA Local Attention
本文由兰州大学信息科学与工程学院、青海省物联网重点实验室、青海师范大学于2024年3.2日发表于ArXiv。为了解决现有的注意力模型在有效利用空间信息方面存在的限制和困难,提出了一种高效的局部注意力ELA模型。该方法通过分析坐标注意力的局限性,作者识别…
迈向未来:内部审计的数字化转型的道与术
目录
前言
一、内部审计的发展阶段
二、内部审计的逻辑架构
三、内部审计数字化转型面临的问题
四、内部审计数字化转型的框架方法
五、内部审计的数字化转型能力体系
六、内部审计的数字化转型路径
七、内部审计的数字化系统平台 前言
内部审计是一种独立的、客观的确…
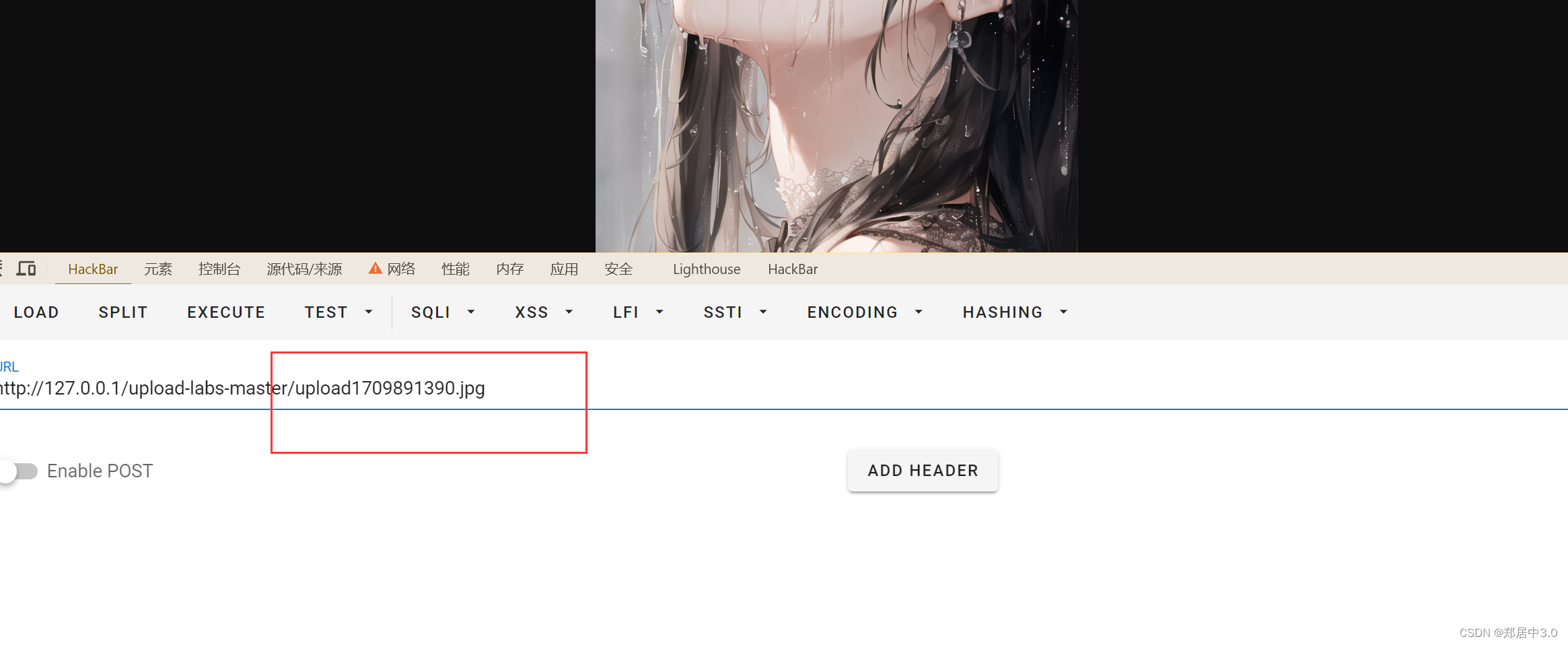
upload-labs通关记录
文章目录 前言 1.pass-012.pass-023.pass-034.pass-045.pass-056.pass-067.pass-078.pass-089.pass-0910.pass-1011.pass-1112.pass-1213.pass-1314.pass-1415.pass-1516.pass-1617.pass-1718.pass-1819.pass-19 前言 本篇文章记录upload-labs中,所有的通过技巧和各…
树莓派(Raspberry Pi)常见的各种引脚介绍
本文将为您详细讲解树莓派(Raspberry Pi)常见的各种引脚,以及它们的特点、区别和优势。树莓派是一款非常受欢迎的单板计算机,它拥有多个 GPIO(通用输入输出)引脚,这些引脚可以用于各种电子项目和…
网站建设大概需要多少钱?费用是多少?怎么样
1、网站建设详细报价单。 建立一个网站需要多少钱?
公司不同,地点不同,技术不同,需求不同,价格也不同。 1、不要尝试用几百块钱建立一个网站,2、几千块做一个普通的网站,3、几万块做一个更好的…
代码随想录第52天| ● 392.判断子序列 ● 115.不同的子序列
文章目录 ● 392.判断子序列思路代码: ● 115.不同的子序列思路:代码: ● 392.判断子序列 思路 递推顺序:从上到下 从左到右
代码:
class Solution {public boolean isSubsequence(String s, String t) {int[][]dpn…
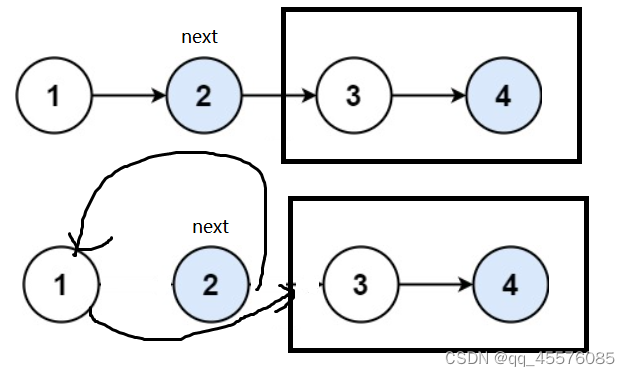
两两交换链表中的节点+力扣
题目
题目链接
. - 力扣(LeetCode)
题目描述 代码实现
class Solution {
public:ListNode* swapPairs(ListNode* head) {if(head nullptr || head->next nullptr) return head;ListNode *tmpHead swapPairs(head->next->next);ListNode …
Vue | 基于 vue-admin-template 项目的跨域问题解决方法
目录
一、现存问题
二、解决方法
2.1 修改的第一个地方
2.2 修改的第二个地方
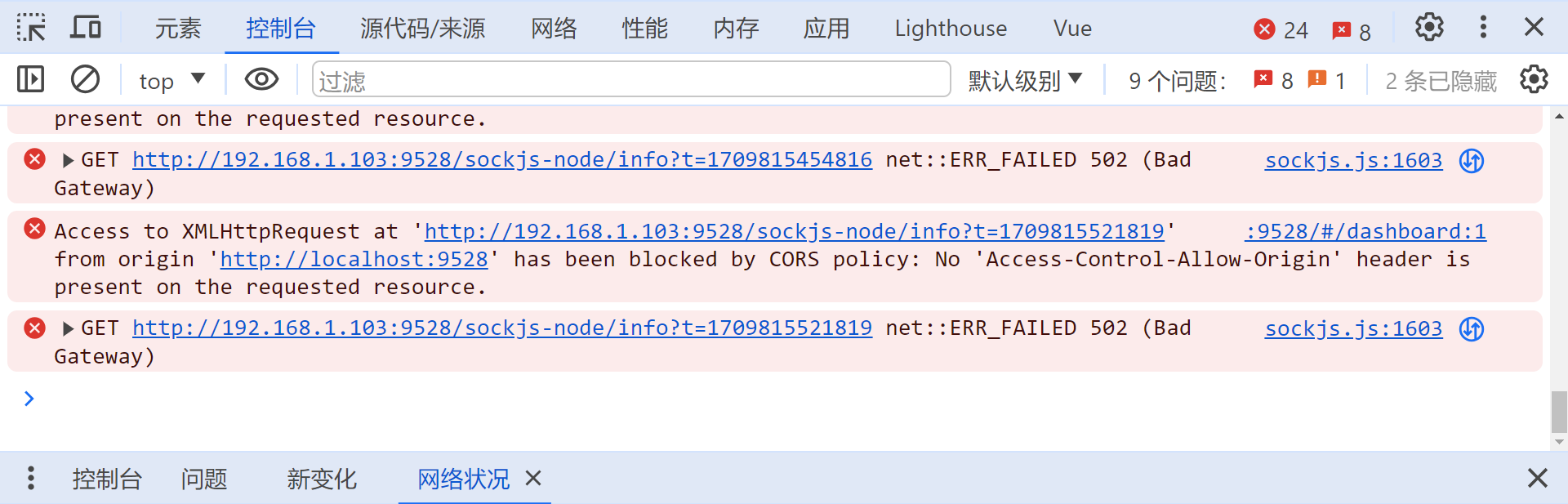
2.3 修改的第三个地方 自存 一、现存问题
报错截图如下: 二、解决方法
2.1 修改的第一个地方
在 .env.development 文件中:
# base api
# VUE_APP_BASE_API /d…
瑞芯微 | I2S-音频基础 -1
最近调试音频驱动,顺便整理学习了一下i2s、alsa相关知识,整理成了几篇文章,后续会陆续更新。
喜欢嵌入式、Li怒晓得老铁可以关注一口君账号。
1. 音频常用术语
名称含义ADC(Analog to Digit Conversion)模拟信号转换…
使用java批量写入环境变量
环境需求
jdk版本:1.8 jna依赖: <dependency><groupId>net.java.dev.jna</groupId><artifactId>jna</artifactId><version>5.10.0</version></dependency><dependency><groupId>net.java.…
git fatal: detected dubious ownership in repository at ‘xxx‘ 彻底解决方法
前言
在 windows 重置后, git 仓库无法正常使用 git 的所有 命令,运行任何 git 命令,都会提示如下:
$ git log
fatal: detected dubious ownership in repository at D:/rk/rk3568/nanopi/uboot-rockchip
D:/rk/rk3568/nanopi/u…
上班族真香副业:工资4500,靠steam游戏搬砖项目月入过w
steam游戏搬砖项目已经存在好多年了,这个项目比较冷门且能持续稳定盈利,是一个非常不错的项目。即使你没玩过steam游戏也没关系,这个steam游戏搬砖项目既不需要你会玩游戏,也不需要你懂英语。 steam游戏搬砖项目的盈利点在汇率差和…
什么才是数字化转型?
数字化转型是指企业或组织利用数字技术(如云计算、大数据、人工智能、物联网等)来改变其业务模式、运营流程、客户体验和企业文化,以提高效率、创新产品和服务、增强竞争力和创造新的增长机会。这一过程通常涉及对现有业务流程的重新设计&…
protobufjs使用教程,支持proto文件打包成typescript或javascript脚本
官方链接:https://docs.cocos.com/creator/manual/zh/scripting/modules/example.html
第一步,安装nodejs。(自行安装)
安装教程可参考 https://www.runoob.com/nodejs/nodejs-install-setup.html
第二步,创建cocos…
C++11_右值引用与移动语义
目录
1、左值的定义
1.1 左值引用
2、右值的定义
2.1 右值引用
3、右值与左值的使用区别
4、右值引用的意义
4.1 左值引用的短板
5、移动语义
5.1 移动构造
5.2 移动赋值
6、万能引用
6.1 右值的别名-左值化
6.2 完美转发 前言: 在C11之前就有了引…
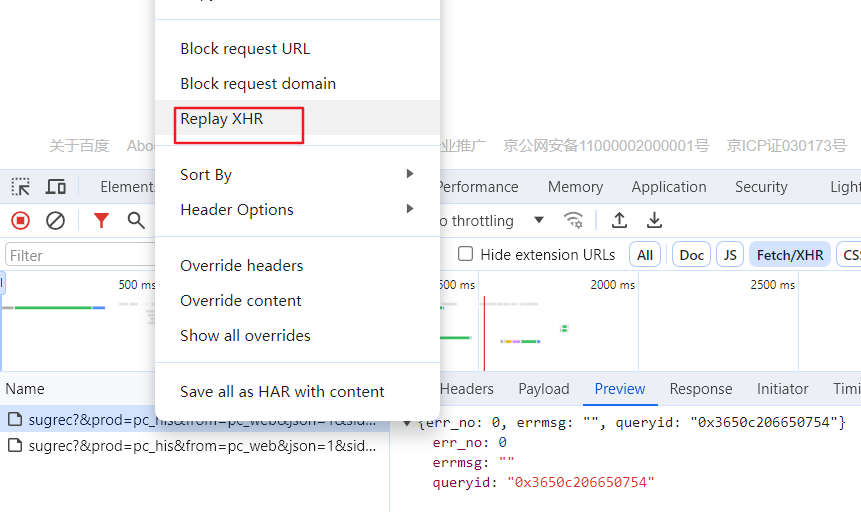
浏览器一键重新发起请求
一、需求场景 在前端开发过程中,经常会需要重新请求后台进行代码调试,之前的常规方法是刷新浏览器页面或者点击页面进行交互,这样对多个请求的场景就很方便,但是往往很多时候我们只是单纯的想重新发起一个请求(多个请求…
c++ 11 新特性 不同数据类型之间转换函数之const_cast
一.不同数据类型之间转换函数const_cast介绍 const_cast是C11中引入的一种类型转换操作符,用于修改类型的const或volatile属性。const_cast的主要用途是移除对象的常量性,它是唯一具有此能力的C风格的转型操作符。在C11中,const_cast可以完成…
YouTube Premium 会员氪金教程
前言
很多小伙伴喜欢看看YouTube但是有些需要会员才可以查看,会员可以免广告,根据个人需求选择是否需要开通
1、点击个人账号的头像,选择“购买内容和会员” 2、选择个人,点击免费试订,第一个月是免费,如…
智能驾驶规划控制理论学习08-自动驾驶控制模块(轨迹跟踪)
目录
一、基于几何的轨迹跟踪方法
1、基本思想
2、纯追踪
3、Stanly Method
二、PID控制器
三、LQR(Linear Quadratic Regulator)
1、基本思想
2、LQR解法
3、案例学习
基于LQR的路径跟踪 基于LQR的速度跟踪 4、MPC(Mode…