文章目录
- 概率密度函数(probability density function,PDF)
- 分布函数(Cumulative Distribution Function,CDF)
- 核密度估计(KDE)
- 经验累计分布函数(Empirical Cumulative Distribution Function,eCDF)
- Kolmogorov–Smirnov test
概率密度函数(probability density function,PDF)
以下解释都来自维基百科:
在数学中,连续型随机变量的概率密度函数(Probability density function),简写作PDF。
是一个描述这个随机变量的输出值,在某个确定的取值点附近的可能性的函数。

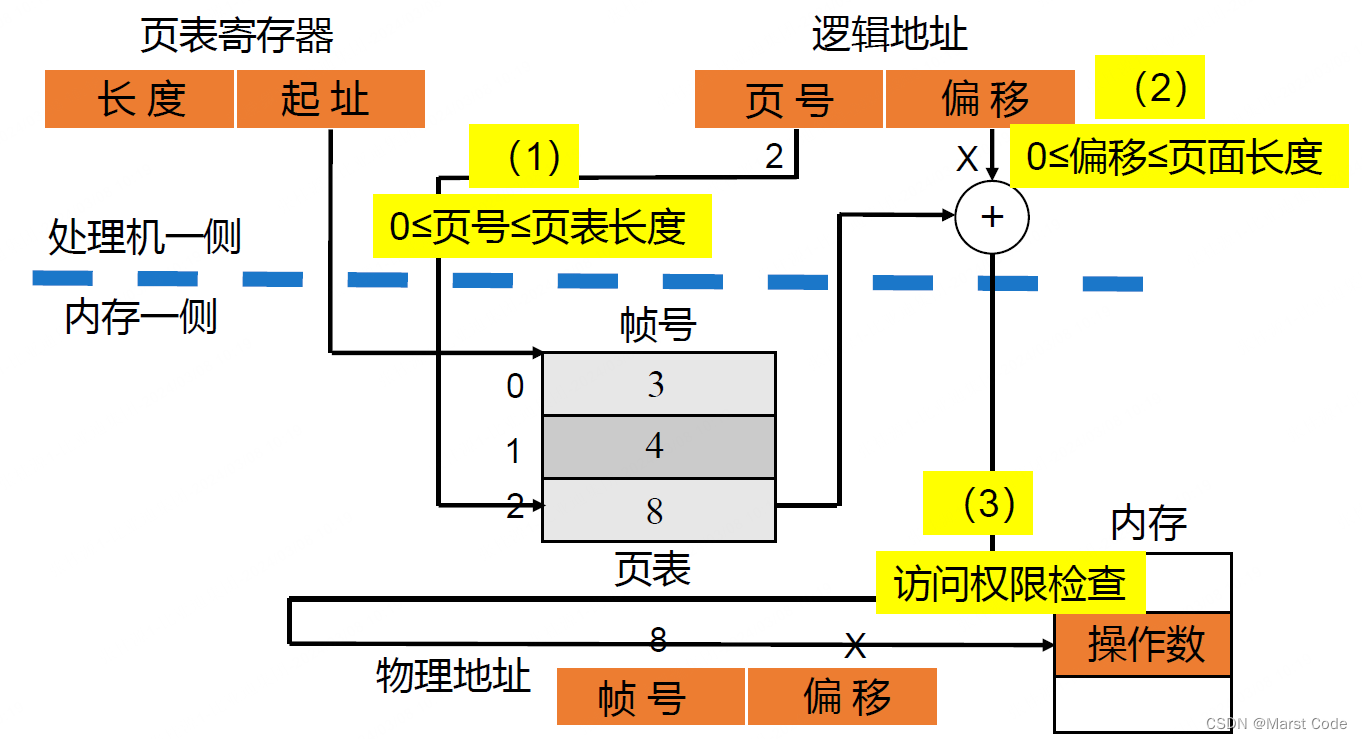
图中,横轴为随机变量的取值,纵轴为概率密度函数的值,而随机变量的取值落在某个区域内的概率为概率密度函数在这个区域上的积分。(实在不能理解,就约等于认为横轴是连续的数值变量,纵轴是每个数值出现的概率)
当概率密度函数存在的时候,累积分布函数是概率密度函数的积分。
分布函数(Cumulative Distribution Function,CDF)
以下解释都来自维基百科:
累积分布函数(cumulative distribution function,CDF)或概率分布函数,简称分布函数,是概率密度函数的积分,能完整描述一个随机变量 X的概率分布。
在标量连续分布的情况下,它给出了从负无穷到X的概率密度函数下的面积。 累积分布函数也用于指定多元随机变量的分布。

通俗点来说就是P(X <= x)的概率即为X的累积分布函数,也就是PDF那副图中的求阴影面积占整个钟形曲线包裹的面积的比例。

核密度估计(KDE)
以下内容来自维基百科:
核密度估计(Kernel density estimation,缩写:KDE)是在概率论中用来估计未知的密度函数,属于非参数检验方法之一

可能看不懂啥意思,人话版如下:
一个变量 x,在样本中多次抽样,得到x1,x2,x3…xn .那么我们可以做一个直方图看一下数值和频次大概是什么样子。

是不是和正态分布的概率密度函数很像?但是不平滑,所以加了一个核函数让x的取值和概率密度的关系更平滑。

上面的蓝色线条就是kernel density的结果。
经验累计分布函数(Empirical Cumulative Distribution Function,eCDF)
简而言之,这是一个根据抽样样本数据来近似总体分布函数的方法。我们从总体中抽出n个样本{x1,x2,x3…xn},对于这个样本我们可以画一个频率密度直方图,并且我们设定每个样本的概率是1/n,于是据此可以画一个该抽样样本的分布函数。
因为样本数目有限,样本变量为离散的,所以这个分布函数是阶梯函数(step function),每一步阶梯的高度都是1/n,代表每个对应的样本数据的概率为1/n,将所有的样本数据爬完后最终到达1。
如果抽样样本足够多的话,eCDF也就越接近总体的CDF。
对于这种阶梯式的step function,被描述为random walk,也就是随机游走,随机游走也是一个统计学概念,在这里,我们考虑一个点从原点出发向右行走,当遇到抽样分布的样本点(数据点)时(对应的横坐标),就向上走1/n,如果没遇到就平行x轴行走。
样本少的时候,就像上述的KDE那里说的,需要核函数平滑概率密度函数,得到概率密度函数后求导得到分布函数/经验累计分布函数。
Kolmogorov–Smirnov test
这是一个非参数检验,通过比较两个抽样样本的eCDF的形状,来检验它们是否来源于同一个总体分布。往往用于检验一个抽样分布是否属于正态分布。
方法很简单,在同一个图上画出两个抽样样本的eCDF(样本数目分别为n、m),然后找到两条阶梯线最大的差距D,这个D就是我们需要的统计量,对于原假设H0:两抽样分布来源于同一总体,D就会很小,如果D过大(α=0.05)就可以拒绝原假设接受备择假设:两抽样分布来源于不同总体。
D本身的分布是通过非常多次改变两样本在x轴上的排序从而计算得到的,每一次打乱样本顺序,都可以计算出相应的一个D,得到一个D的分布,这样就可以考察现在的D的水平是否满足p<0.05。因为对于eCDF来说,确定样本量后,阶梯上升量就确定了,所以改变eCDF形状的因素就只剩下样本在x轴上的分布情况。