目录
- 一. 软间隔模型
- 1. 松弛因子的解释
- 小节
- 2. SVM软间隔模型总结
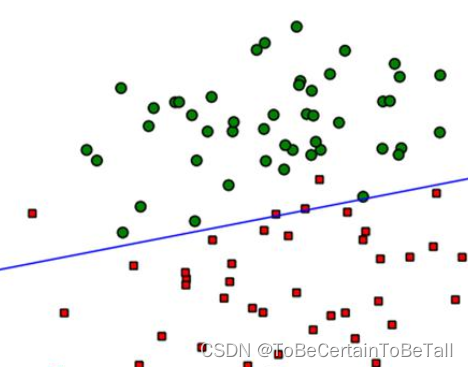
线性可分SVM中,若想找到分类的超平面,数据必须是线性可分的;但在实际情况中,线性数据集存在少量的异常点,导致SVM无法对数据集线性划分
也就是说:正常数据本身是线性可分的,但是由于存在异常点数据,导致数据集不能够线性可分
一. 软间隔模型
为了解决上述问题,我们引入软间隔的概念:
1. 松弛因子的解释
- 硬间隔: 线性划分SVM中的硬间隔是距离度量;在线性划分SVM中,要求函数距离一定是大于等于1的,最大化硬间隔条件为: { m i n 1 2 ∥ w → ∥ 2 s . t : y ( i ) ( ω T ⋅ x ( i ) + b ) ≥ 1 , i = 1 , 2 , . . . , m \left\{\begin{matrix}min\frac{1}{2}\left \| \overrightarrow{w} \right \| ^{2} \\s.t: y^{(i)} (\omega ^{T}\cdot x^{(i)} +b)\ge1,i=1,2,...,m \end{matrix}\right. {min21 w 2s.t:y(i)(ωT⋅x(i)+b)≥1,i=1,2,...,m
- 软间隔:SVM对于训练集中的每个样本都引入一个松弛因子(ξ),使得函数距离加上松弛因子后的值是大于等于1; y ( i ) ( ω T ⋅ x ( i ) + b ) ≥ 1 − ξ ; i = 1 , 2 , . . . , m , ξ ≥ 0 y^{(i)} (\omega ^{T}\cdot x^{(i)} +b)\ge1-\xi ;i=1,2,...,m,\xi\ge 0 y(i)(ωT⋅x(i)+b)≥1−ξ;i=1,2,...,m,ξ≥0
松弛因子(ξ)表示:相对于硬间隔,对样本到超平面距离的要求放松了
当 ξ = 0 ξ=0 ξ=0 , 相当于硬间隔
当 0 < ξ < 1 0<ξ<1 0<ξ<1 , 相当于样本点位于“街”内
当 ξ > 1 ξ>1 ξ>1 , 相当于样本点位于“街”对面
当 ξ > 2 ξ>2 ξ>2 , 相当于样本点位于“街”对面外侧注意: ξ ξ ξ只能对少量的样本起作用
ξ ξ ξ越大,表示样本点离超平面越近,
ξ > 1 ξ>1 ξ>1,那么表示允许该样本点分错因此:加入松弛因子是有成本的,过大的松弛因子可能会导致模型分类错误
所以,我们对存有异常点的数据集划分时,目标函数就变成了:
{
m
i
n
1
2
∥
w
→
∥
2
+
C
∑
i
=
1
n
ξ
(
i
)
y
(
i
)
(
ω
T
⋅
x
(
i
)
+
b
)
≥
1
−
ξ
(
i
)
,
i
=
1
,
2
,
.
.
.
,
m
\left\{\begin{matrix}min\frac{1}{2}\left \| \overrightarrow{w} \right \| ^{2}+C\sum_{i=1}^{n} \xi _{(i)} \\ \\y^{(i)} (\omega ^{T}\cdot x^{(i)} +b)\ge1-\xi ^{(i)} ,i=1,2,...,m \end{matrix}\right.
⎩
⎨
⎧min21
w
2+C∑i=1nξ(i)y(i)(ωT⋅x(i)+b)≥1−ξ(i),i=1,2,...,m
ξ
i
≥
0
,
i
=
1
,
2
,
.
.
.
,
m
\xi{i}\ge 0,i=1,2,...,m
ξi≥0,i=1,2,...,m
公式 C ∑ i = 1 n ξ ( i ) C\sum_{i=1}^{n} \xi _{(i)} C∑i=1nξ(i)表式:
每个样本惩罚项的总和不能大,函数中的C>0是惩罚参数,需要调参C越大,表示对错误分类的惩罚越大,也就越不允许存在分错的样本;
C越小表示对误分类的惩罚越小,也就是表示允许更多的分错样本存在也就是说:
对于完全线性可分的数据来说,C的值可以给大一点
对于线性可分但存在异常的数据来说,C的值需要调小
小节
对于线性可分的m个样本(x1,y1),(x2,y2)… :
x为n维的特征向量
y为二元输出,即+1,-1
SVM的输出为w,b,分类决策函数
选择一个惩罚系数C>0,构造约束优化问题
{
min
β
≥
0
1
2
∑
i
=
1
m
∑
j
=
1
m
β
i
β
j
y
(
i
)
y
(
j
)
x
(
j
)
T
x
(
i
)
−
∑
i
=
1
m
β
i
s
.
t
:
∑
i
=
1
m
β
i
y
(
i
)
=
0
,
0
≤
β
i
≤
C
,
i
=
1
,
2
,
.
.
.
,
m
\left\{\begin{matrix}\min_{\beta \ge 0}\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m} \beta _{i}\beta _{j} y^{(i)}y^{(j)}x^{(j)^{T}} x^{(i)}-\sum_{i=1}^{m} \beta _{i} \\s.t:\sum_{i=1}^{m} \beta _{i} y^{(i)}=0,0\le \beta _{i}\le C,i=1,2,...,m \end{matrix}\right.
{minβ≥021∑i=1m∑j=1mβiβjy(i)y(j)x(j)Tx(i)−∑i=1mβis.t:∑i=1mβiy(i)=0,0≤βi≤C,i=1,2,...,m
使用SMO算法求出上述最优解
β
\beta
β
找到所有支持向量集合:
S
=
(
x
(
i
)
,
y
(
i
)
)
(
0
<
β
i
<
C
,
i
=
1
,
2
,
.
.
.
,
m
)
S = (x^{(i)}, y^{(i)}) (0<\beta_{i} < C,i=1,2,...,m)
S=(x(i),y(i))(0<βi<C,i=1,2,...,m)
从而更新w,b
w = ∑ i = 1 m β i x ( i ) y ( i ) w=\sum_{i=1}^{m} \beta _{i} x^{(i)}y^{(i)} w=∑i=1mβix(i)y(i)
b = 1 S ∑ i = 1 S ( y s − ∑ i = 1 m β i x ( i ) T y ( i ) x s ) b=\frac{1}{S} \sum_{i=1}^{S}(y^{s}- \sum_{i=1}^{m} \beta _{i} x^{(i)^{T}}y^{(i)}x^{s} ) b=S1∑i=1S(ys−∑i=1mβix(i)Ty(i)xs)
构造最终的分类器,为:
f
(
x
)
=
s
i
g
n
(
w
∗
x
+
b
)
f(x)=sign(w\ast x+b)
f(x)=sign(w∗x+b)
x<0时,y=-1
x=0时,y=0
x>0时,y=1
注意:
假设,不会出现0
若出现,正负样本随意输出一个,即+0.00000001或-0.00000001都可以
2. SVM软间隔模型总结
可以解决线性数据中存在异常点的分类模型构建问题
通过引入松弛因子,可以增加模型的泛化能力,即鲁棒性;
对于模型而言:
如果给定的惩罚项系数C越小,表示在模型构建的时候,就允许存在越多的分类错误的样本,也就表示此时模型的准确率会比较低;
如果惩罚项系数越大,表示在模型构建的时候,就越不允许存在分类错误的样本,也就表示此时模型的准确率会比较高。
感谢阅读🌼
如果喜欢这篇文章,记得点赞👍和转发🔄哦!
有任何想法或问题,欢迎留言交流💬,我们下次见!
祝愉快🌟!